Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T05:46:59.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex flows of moist air with non-equilibrium and homogeneous condensation

Published online by Cambridge University Press:  07 January 2020

Zvi Rusak Open the ORCID record for Zvi Rusak [Opens in a new window] ,
Gerald A. Rawcliffe  and
Yuxin Zhang
Zvi Rusak*
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY12180-3590, USA
Gerald A. Rawcliffe
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY12180-3590, USA
Yuxin Zhang
Affiliation:
Department of Mechanical Engineering, Washington State University, Richland, WA99354, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

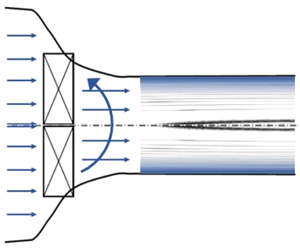
A small-disturbance model is presented for the complex dynamics of vortex flows of moist air in a straight, circular pipe with non-equilibrium and homogeneous condensation. The model explores the nonlinear interactions among the vortex near-critical swirl ratio and the small amount of water vapour in the air. The condensation rate is calculated according to classical nucleation and droplet growth models. The asymptotic analysis gives the similarity parameters that govern the flow problem. These are the flow inlet swirl ratio $\unicode[STIX]{x1D714}$, the inlet Mach number $Ma_{0}$, the initial humidity $\tilde{\unicode[STIX]{x1D714}}_{0}$, the number of water molecules in a characteristic fluid element $n_{C}$, the inlet centreline super-saturation ratio $S_{0}$ and the ratio of characteristic condensation and flow time scales $K$. Also, the flow field may be described by an ordinary first-order nonlinear differential equation for the flow evolution coupled with a set of four first-order ordinary differential equations along the pipe for the calculation of the condensate mass fraction. An iterative numerical scheme which combines the Runge–Kutta integration technique for the flow dynamics with Simpson’s integration rule for the calculation of the condensation variables is developed. Specifically, equilibrium states are determined, including the possibility of the appearance of multiple states under the same boundary conditions, and the stability characteristics of these states are described. The model is used to study the effects of humidity and of energy supply from nanoscale condensation processes on the large-scale dynamics of vortex flows as well as the effect of flow swirl on condensation processes in swirling flows.

JFM classification

Vortex Flows: Vortex instability Compressible Flows: Compressible Flows Multiphase and Particle-laden Flows: Reacting multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A38
Copyright
© 2020 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, F. F. 1974 Homogeneous Nucleation Theory. Academic.Google Scholar
Althaus, W., Brucker, Ch. & Weimer, M. 1995 Breakdown of slender vortices. In Fluid Vortices, pp. 373–426. Springer.CrossRefGoogle Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.CrossRefGoogle Scholar
Beran, P. S. 1994 The time-asymptotic behavior of vortex breakdown in tubes. Comput. Fluids 23 (7), 913–937.CrossRefGoogle Scholar
Beran, P. S. & Culick, F. E. C. 1992 The role of non-uniqueness in the development of vortex breakdown in tubes. J. Fluid Mech. 242, 491–527.CrossRefGoogle Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.CrossRefGoogle Scholar
Darmofal, D. L. 1996 Comparisons of experimental and numerical results for axisymmetric vortex breakdown in pipes. Comput. Fluids 25 (4), 353–371.CrossRefGoogle Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4 (1), 195–218.CrossRefGoogle Scholar
Hill, P. G. 1966 Condensation of water vapour during supersonic expansion in nozzles. J. Fluid Mech. 25 (3), 593–620.CrossRefGoogle Scholar
Keller, J. J., Egli, W. & Exley, J. 1985 Force-and loss-free transitions between flow states. Z. Angew. Math. Phys. 36 (6), 854–889.CrossRefGoogle Scholar
Leclaire, B. & Jacquin, L. 2012 On the generation of swirling jets: high-Reynolds-number rotating flow in a pipe with a final contraction. J. Fluid Mech. 692, 78–111.CrossRefGoogle Scholar
Leibovich, S. 1984 Vortex stability & breakdown: survey and extension. AIAA J. 22 (9), 1192–1206.CrossRefGoogle Scholar
Lopez, J. M. 1994 On the bifurcation structure of axisymmetric vortex breakdown in a constricted pipe. Phys. Fluids 6 (11), 3683–3693.CrossRefGoogle Scholar
Lucca-Negro, O. & O’doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27 (4), 431–481.CrossRefGoogle Scholar
Malkiel, E., Cohen, J., Rusak, Z. & Wang, S. 1996 Axisymmetric vortex breakdown in a pipe: theoretical and experimental studies. In Proceedings of the 36th Israel Annual Conference on Aerospace Sciences, (February), pp. 24–34. Technion, Haifa.Google Scholar
Mattner, T. W., Joubert, P. N. & Chong, M. S. 2002 Vortical flow. Part 1. Flow through a constant-diameter pipe. J. Fluid Mech. 463, 259–291.CrossRefGoogle Scholar
Meliga, P., Gallaire, F. & Chomaz, J. M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C. O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.CrossRefGoogle Scholar
Panda, J. & McLaughlin, D. K. 1994 Experiments on the instabilities of a swirling jet. Phys. Fluids 6 (1), 263–276.CrossRefGoogle Scholar
Peters, F. 1983 A new method to measure homogeneous nucleation rates in shock tubes. Exp. Fluids 1 (3), 143–148.CrossRefGoogle Scholar
Peters, F. & Paikert, B. 1989 Nucleation and growth rates of homogeneously condensing water vapour in argon from shock tube experiments. Exp. Fluids 7, 521–530.CrossRefGoogle Scholar
Pruppacher, H. R. & Klett, J. D. 1980 Microphysics of Clouds and Precipitation, Chap. 2, pp. 9–21. D. Reidel.Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.CrossRefGoogle Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Rusak, Z.2000 Review of recent studies on the axisymmetric vortex breakdown phenomenon. In AIAA Fluids 2000 Conference, AIAA Paper 2000-2529.Google Scholar
Rusak, Z., Choi, J. J. & Lee, J.-H. 2007 Bifurcation and stability of near-critical compressible swirling flows. Phys. Fluids 19 (11), 114107.CrossRefGoogle Scholar
Rusak, Z., Choi, J. J., Bourquard, N. & Wang, S. 2015 Vortex breakdown of compressible subsonic swirling flows in a finite-length straight circular pipe. J. Fluid Mech. 781, 3–27.CrossRefGoogle Scholar
Rusak, Z., Kapila, A. K. & Choi, J. J. 2002 Effect of combustion on near-critical swirling flow. Combust. Theor. Model. 6 (4), 625–645.CrossRefGoogle Scholar
Rusak, Z. & Lee, J. C. 2000 Transonic flow of moist air around a thin airfoil with nonequilibrium and homogeneous condensation. J. Fluid Mech. 403, 173–199.CrossRefGoogle Scholar
Rusak, Z. & Lee, J. H. 2004 On the stability of a compressible axisymmetric rotating flow in a pipe. J. Fluid Mech. 501, 25–42.CrossRefGoogle Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of a near-critical swirling flow in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.CrossRefGoogle Scholar
Rusak, Z., Whiting, C. H. & Wang, S. 1998 Axisymmetric breakdown of a Q-vortex in a pipe. AIAA J. 36 (10), 1848–1853.CrossRefGoogle Scholar
Rusak, Z., Zhang, Y., Lee, H. & Wang, S. 2017 Swirling flow states in finite-length diverging or contracting circular pipes. J. Fluid Mech. 819, 678–712.CrossRefGoogle Scholar
Schnerr, G. H. & Dohrmann, U. 1990 Transonic flow around airfoils with relaxation and energy supply by homogeneous condensation. AIAA J. 28 (7), 1187–1193.CrossRefGoogle Scholar
Schnerr, G. H. & Dohrmann, U. 1994 Drag and lift in nonadiabatic transonic flow. AIAA J. 32 (1), 101–107.CrossRefGoogle Scholar
Snyder, D. O. & Spall, R. E. 2000 Numerical simulation of bubble-type vortex breakdown within a tube-and-vane apparatus. Phys. Fluids 12 (3), 603–608.CrossRefGoogle Scholar
Spall, R. E., Gatski, T. B. & Grosch, C. E. 1987 A criterion for vortex breakdown. Phys. Fluids 30 (11), 3434–3440.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Umeh, C. O. U., Rusak, Z., Gutmark, E., Villalva, R. & Cha, D. J. 2010 Experimental and computational study of nonreacting vortex breakdown in a swirl-stabilized combustor. AIAA J. 48 (11), 2576–2585.CrossRefGoogle Scholar
Vanierschot, M. 2017 On the dynamics of the transition to vortex breakdown in axisymmetric inviscid swirling flows. Eur. J. Mech. (B/Fluids) 65, 65–69.CrossRefGoogle Scholar
Wang, S. & Rusak, Z. 1996 On the stability of an axisymmetric rotating flow in a pipe. Phys. Fluids 8 (4), 1007–1016.CrossRefGoogle Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.CrossRefGoogle Scholar
Wegener, P. P. 1975 Non-equilibrium flow with condensation. Acta Mechanica 21 (1-2), 65–91.CrossRefGoogle Scholar
Wegener, P. P. & Mack, L. M. 1958 Condensation in supersonic and hypersonic wind tunnels. Adv. Appl. Mech. 5, 307–447 Elsevier.CrossRefGoogle Scholar
Wegener, P. P. & Pouring, A. A. 1964 Experiments on condensation of water vapor by homogeneous nucleation in nozzles. Phys. Fluids 7 (3), 352–361.CrossRefGoogle Scholar
Zettlemoyer, A. C. 1969 Nucleation. Marcel Dekker.Google Scholar
Supplementary material: File

Rusak et al. supplementary material

Rusak et al. supplementary material

Download Rusak et al. supplementary material(File)
File 52 KB