Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T22:13:48.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex events in Euler and Navier–Stokes simulations with smooth initial conditions

Published online by Cambridge University Press:  23 November 2011

P. Orlandi ,
S. Pirozzoli  and
G. F. Carnevale
P. Orlandi*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università La Sapienza, via Eudossiana 16, I-00184, Roma
S. Pirozzoli
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università La Sapienza, via Eudossiana 16, I-00184, Roma
G. F. Carnevale
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università La Sapienza, via Eudossiana 16, I-00184, Roma Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present high-resolution numerical simulations of the Euler and Navier–Stokes equations for a pair of colliding dipoles. We study the possible approach to a finite-time singularity for the Euler equations, and contrast it with the formation of developed turbulence for the Navier–Stokes equations. We present numerical evidence that seems to suggest the existence of a blow-up of the inviscid velocity field at a finite time (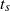) with scaling , 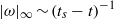. This blow-up is associated with the formation of a 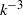spectral range, at least for the finite range of wavenumbers that are resolved by our computation. In the evolution toward 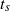, the total enstrophy is observed to increase at a slower rate, 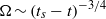, than would naively be expected given the behaviour of the maximum vorticity, 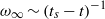. This indicates that the blow-up would be concentrated in narrow regions of the flow field. We show that these regions have sheet-like structure. Viscous simulations, performed at various 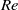, support the conclusion that any non-zero viscosity prevents blow-up in finite time and results in the formation of a dissipative exponential range in a time interval around the estimated inviscid 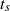. In this case the total enstrophy saturates, and the energy spectrum becomes less steep, approaching 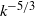. The simulations show that the peak value of the enstrophy scales as 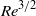, which is in accord with Kolmogorov phenomenology. During the short time interval leading to the formation of an inertial range, the total energy dissipation rate shows a clear tendency to become independent of 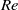, supporting the validity of Kolmogorov’s law of finite energy dissipation. At later times the kinetic energy shows a 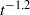decay for all 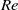, in agreement with experimental results for grid turbulence. Visualization of the vortical structures associated with the stages of vorticity amplification and saturation show that, prior to 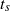, large-scale and the small-scale vortical structures are well separated. This suggests that, during this stage, the energy transfer mechanism is non-local both in wavenumber and in physical space. On the other hand, as the spectrum becomes shallower and a 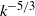range appears, the energy-containing eddies and the small-scale vortices tend to be concentrated in the same regions, and structures with a wide range of sizes are observed, suggesting that the formation of an inertial range is accompanied by transfer of energy that is local in both physical and spectral space.

JFM classification

Turbulent Flows: Turbulence simulation Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 690 , 10 January 2012 , pp. 288 - 320
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. K. 1967 An Introduction to Fluid Dynamics, p. 617. Cambridge University Press.Google Scholar
2. Beale, J. T., Kato, T. & Majda, A. 1984 A remark on the breakdown of smooth solutions of the 3D Euler equations. Commun. Math. Phys. 94, 61–66.Google Scholar
3. Bell, J. B. & Marcus, D. L. 1992 Vorticity intensification and transition to turbulence in three-dimensional Euler equations. Commun. Math Phys. 147, 371–394.Google Scholar
4. Brachet, M. E. 1991 Direct simulation of three-dimensional turbulence in the Taylor–Green vortex. Fluid Dyn. Res. 8, 1–8.CrossRefGoogle Scholar
5. Brachet, M. E., Meiron, D. I., Orszag, S. A., Nickel, B. G., Morf, R. H. & Frisch, U. 1983 Small-scale structure of the Taylor–Green vortex. J. Fluid Mech. 130, 411–452.CrossRefGoogle Scholar
6. Bustamante, M. D. & Kerr, R. M. 2008 3D Euler about a 2D symmetry plane. Physica D 237, 1912–1920.CrossRefGoogle Scholar
7. Cadot, O., Douady, S. & Couder, Y. 1995 Characterization of the low-pressure filaments in a three-dimensional turbulent shear flow. Phys. Fluids 7, 630–646.CrossRefGoogle Scholar
8. Cichowlas, C. & Brachet, M. 2005 Evolution of complex singularities in Kida–Pelz and Taylor–Green inviscid flows. Fluid Dyn. Res. 36, 239–248.CrossRefGoogle Scholar
9. Cichowlas, C., Debbashn, F. & Brachet, M. 2006 Evolution of complex singularities and Kolmogorov scaling in truncated three-dimensional Euler flows. In IUTAM Symposium on Elementary Vortices and Coherent Structures: Significance in Turbulence Dynamics, pp. 319–328. Springer.CrossRefGoogle Scholar
10. Constantin, P. 1994 Geometric statistics in turbulence. SIAM Rev. 36, 73–98.Google Scholar
11. Crocco, L. & Orlandi, P. 1985 A transformation for the energy-transfer term in isotropic turbulence. J. Fluid Mech. 161, 405–424.Google Scholar
12. Domaradzki, J. & Rogallo, R. S. 1990 Local energy transfer and non-local interactions in homogeneous, isotropic turbulence. Phys. Fluids A 2–3, 413–426.CrossRefGoogle Scholar
13. Duponcheel, M., Orlandi, P. & Winckelmans, G. 2008 Time-reversibility of the Euler equations as a benchmark for energy conserving schemes. J. Comp. Phys. 227, 8736–8752.CrossRefGoogle Scholar
14. Frisch, U. 1995 Turbulence. Cambridge University Press.CrossRefGoogle Scholar
15. Galaktionov, V. A. 2009 On blow-up twistors for the Navier–Stokes equations in R3. arXiv:0901.4286.Google Scholar
16. George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids 4, 1492–1509.CrossRefGoogle Scholar
17. Gibbon, J. D. 2008 The three-dimensional Euler equations: where do we stand? Physica D 237, 14–17.CrossRefGoogle Scholar
18. Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 3, 1065–1081.Google Scholar
19. Horiuti, K. & Fujisawa, Y. 2008 The multi-mode stretched spiral vortex in homogeneous isotropic turbulence. J. Fluid Mech. 595, 341–366.CrossRefGoogle Scholar
20. Hou, T. Y. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3D incompressible Euler equations. J. Nonlinear Sci. 16, 639–664.CrossRefGoogle Scholar
21. Hou, T. Y. & Li, R. 2008 Blowup or no blowup? The interplay between theory and numerics. Physica D 237, 1937–1944.CrossRefGoogle Scholar
22. Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
23. Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90 the data are available in AGARD AR-345 1998.CrossRefGoogle Scholar
24. Kerr, R. M. 1993 Evidence for a singularity of the three-dimensional, incompressible Euler equations. Phys. Fluids A 5, 1725–1746.CrossRefGoogle Scholar
25. Kerr, R. M. 2001 A new role for vorticity and singular dynamics in turbulence. In Nonlinear Instability Analysis, Volume II (ed. Debnath, L. ), pp. 15–68. WIT Press.Google Scholar
26. Kerr, R. M. 2006 Computational Euler history. arXiv:physics/0607148v2  [physics.flu-dyn].Google Scholar
27. Kraichnan, R. H. 1971 Inertial range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.Google Scholar
28. Kolmogorov, A. N. 1942 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. A 434, 9–13.Google Scholar
29. Lamb, H. 1932 Hydrodynamics, p. 738. Cambridge University Press.Google Scholar
30. Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.CrossRefGoogle Scholar
31. Lu, L. & Doering, C. R. 2008 Limits of enstrophy growth for solution of the three-dimensional Navier–Stokes equations. Indiana Univ. Math. J. 57, 2693–2728.CrossRefGoogle Scholar
32. Majda, A. J. & Bertozzi, A. L. 2002 Vorticity and Incompressible Flow. Cambridge University Press.Google Scholar
33. Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson Kolmogorov cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
34. Orlandi, P. 2000 Fluid Flow Phenomena: A Numerical Toolkit. Kluwer.CrossRefGoogle Scholar
35. Orlandi, P. 2009 Energy spectra power laws and structures. J. Fluid Mech. 623, 353–374.Google Scholar
36. Orlandi, P. & Carnevale, G. F. 2007 Nonlinear amplification of vorticity in inviscid interaction of orthogonal Lamb dipoles. Phys. Fluids 19 (5), 057106.Google Scholar
37. Orlandi, P. & Pirozzoli, S. 2010 Vorticity dynamics in turbulence growth. Theoret. Comput. Fluid Dyn. 24, 247–251.Google Scholar
38. Pumir, A. & Siggia, E. 1990 Collapsing solutions to the 3D Euler equations. Phys. Fluids A 2, 220–241.CrossRefGoogle Scholar