Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Noyon, T. A.
Tay, W. B.
van Oudheusden, B. W.
and
Bijl, H.
2014.
Effect of Chordwise Deformation on Unsteady Aerodynamic Mechanisms in Hovering Flapping Flight.
International Journal of Micro Air Vehicles,
Vol. 6,
Issue. 4,
p.
265.
Schlueter-Kuck, Kristy L.
and
Dabiri, John O.
2017.
Coherent structure colouring: identification of coherent structures from sparse data using graph theory.
Journal of Fluid Mechanics,
Vol. 811,
Issue. ,
p.
468.
Kang, Linlin
Liu, Luoqin
Su, Weidong
and
Wu, Jiezhi
2017.
A minimum-domain impulse theory for unsteady aerodynamic force with discrete wake.
Theoretical and Applied Mechanics Letters,
Vol. 7,
Issue. 5,
p.
306.
Lee, Jeongsu
Park, Yong-Jai
Cho, Kyu-Jin
Kim, Daegyoum
and
Kim, Ho-Young
2017.
Hydrodynamic advantages of a low aspect-ratio flapping foil.
Journal of Fluids and Structures,
Vol. 71,
Issue. ,
p.
70.
Martin, Nathan
Roh, Chris
Idrees, Suhail
and
Gharib, Morteza
2017.
To flap or not to flap: comparison between flapping and clapping propulsions.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
Wu, Jiezhi
Liu, Luoqin
and
Liu, Tianshu
2018.
Fundamental theories of aerodynamic force in viscous and compressible complex flows.
Progress in Aerospace Sciences,
Vol. 99,
Issue. ,
p.
27.
Discetti, Stefano
and
Coletti, Filippo
2018.
Volumetric velocimetry for fluid flows.
Measurement Science and Technology,
Vol. 29,
Issue. 4,
p.
042001.
Liu, Luo-Qin
2018.
Unified Theoretical Foundations of Lift and Drag in Viscous and Compressible External Flows.
p.
1.
Kang, L. L.
Liu, L. Q.
Su, W. D.
and
Wu, J. Z.
2018.
Minimum-domain impulse theory for unsteady aerodynamic force.
Physics of Fluids,
Vol. 30,
Issue. 1,
Das, Prashant
Govardhan, R. N.
and
Arakeri, J. H.
2018.
Unsteady two-dimensional jet with flexible flaps at the channel exit.
Journal of Fluid Mechanics,
Vol. 845,
Issue. ,
p.
462.
Jung, Sung Yong
Kim, Jeong Jae
Park, Han Wook
and
Lee, Sang Joon
2018.
Comparison of flow structures behind rigid and flexible finite cylinders.
International Journal of Mechanical Sciences,
Vol. 142-143,
Issue. ,
p.
480.
Iacobello, Giovanni
Scarsoglio, Stefania
Kuerten, J. G. M.
and
Ridolfi, Luca
2019.
Lagrangian network analysis of turbulent mixing.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
p.
546.
Siala, Firas F.
and
Liburdy, James A.
2019.
Leading-edge vortex dynamics and impulse-based lift force analysis of oscillating airfoils.
Experiments in Fluids,
Vol. 60,
Issue. 10,
You, Jiho
Lee, Jinmo
Hong, Seungpyo
and
You, Donghyun
2019.
Optimization of Biomimetic Propulsive Kinematics of a Flexible Foil Using Integrated Computational Fluid Dynamics–Computational Structural Dynamics Simulations.
Journal of Fluids Engineering,
Vol. 141,
Issue. 6,
Wang, Shizhao
He, Guowei
and
Liu, Tianshu
2019.
Estimating lift from wake velocity data in flapping flight.
Journal of Fluid Mechanics,
Vol. 868,
Issue. ,
p.
501.
Zhang, JiaoLong
Hu, Jun
Yu, Yong
and
Xuan, HaiBin
2020.
On the stabilization of leading-edge vortices with different reduced frequencies over finite-aspect-ratio pitch-up wings.
AIP Advances,
Vol. 10,
Issue. 2,
Lee, HyeonKyun
Jang, JinWoo
and
Lee, SangHwan
2020.
An investigation of kinematic parameters and stroke function on stroke reversal for three-dimensional vortex structures around a flapping insect wing.
European Journal of Mechanics - B/Fluids,
Vol. 79,
Issue. ,
p.
165.
Siala, Firas F.
and
Liburdy, James A.
2020.
Power estimation of flapping foil energy harvesters using vortex impulse theory.
Renewable Energy,
Vol. 154,
Issue. ,
p.
894.
Benabed, Ahmed
Limam, Karim
Janssens, Bart
Bosschaerts, Walter
and
Vercauteren, Jan
2020.
Experimental investigation of the flow field generated by idealized human foot tapping.
Science and Technology for the Built Environment,
Vol. 26,
Issue. 2,
p.
229.
Balta, Miquel
Deb, Dipan
and
Taha, Haithem E
2021.
Flow visualization and force measurement of the clapping effect in bio-inspired flying robots.
Bioinspiration & Biomimetics,
Vol. 16,
Issue. 6,
p.
066020.
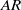 $AR$) and stroke angles were investigated. Experiments were performed with a pair of hinged rectangular plates that were rotated symmetrically in a static fluid, and defocusing digital particle image velocimetry was employed to measure the three-dimensional flow field. Single-plate cases were also studied to compare with clapping plate cases. As
$AR$) and stroke angles were investigated. Experiments were performed with a pair of hinged rectangular plates that were rotated symmetrically in a static fluid, and defocusing digital particle image velocimetry was employed to measure the three-dimensional flow field. Single-plate cases were also studied to compare with clapping plate cases. As 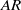 $AR$ decreases, both circulation of the tip vortex and area enclosed by the vortex loop increase inversely. An empirical power-law relationship with a negative exponent is found between total impulse and
$AR$ decreases, both circulation of the tip vortex and area enclosed by the vortex loop increase inversely. An empirical power-law relationship with a negative exponent is found between total impulse and 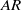 $AR$ for a given stroke angle. The sensitivity of the force generated by the plates to the change of
$AR$ for a given stroke angle. The sensitivity of the force generated by the plates to the change of 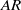 $AR$ is larger at the smaller stroke angle because of faster acceleration and deceleration. The increase in impulse per plate from the single-plate case to the clapping double-plate case is larger for lower
$AR$ is larger at the smaller stroke angle because of faster acceleration and deceleration. The increase in impulse per plate from the single-plate case to the clapping double-plate case is larger for lower 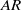 $AR$. These results reveal that low
$AR$. These results reveal that low 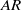 $AR$ wings are more efficient in propulsive force generation in some specific modes of unsteady flapping flight. The evolution of the wake structures is found to depend on
$AR$ wings are more efficient in propulsive force generation in some specific modes of unsteady flapping flight. The evolution of the wake structures is found to depend on 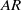 $AR$ and stroke angle.
$AR$ and stroke angle.