Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Samimy, Mo
Webb, Nathan
and
Crawley, Michael
2018.
Excitation of Free Shear-Layer Instabilities for High-Speed Flow Control.
AIAA Journal,
Vol. 56,
Issue. 5,
p.
1770.
Samimy, Mo
Webb, Nathan
and
Esfahani, Ata
2019.
Reinventing the wheel: excitation of flow instabilities for active flow control using plasma actuators.
Journal of Physics D: Applied Physics,
Vol. 52,
Issue. 35,
p.
354002.
Esfahani, Ata
Webb, Nathan
and
Samimy, Mo
2019.
Flow Separation Control over a Thin Post-Stall Airfoil: Effects of Excitation Frequency.
AIAA Journal,
Vol. 57,
Issue. 5,
p.
1826.
Wu, Xuesong
and
Zhang, Zhongyu
2019.
First-principle description of acoustic radiation of shear flows.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 377,
Issue. 2159,
p.
20190077.
Edgington-Mitchell, Daniel
2019.
Aeroacoustic resonance and self-excitation in screeching and impinging supersonic jets – A review.
International Journal of Aeroacoustics,
Vol. 18,
Issue. 2-3,
p.
118.
Feng, Feng
Meng, Xiannan
Guo, Li
and
Wang, Qiang
2020.
Directivity of acoustic field generated by leapfrogging vortices.
Physics of Fluids,
Vol. 32,
Issue. 12,
Zhang, Zhongyu
and
Wu, Xuesong
2020.
Nonlinear evolution and acoustic radiation of coherent structures in subsonic turbulent free shear layers.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Bell, G.
Cluts, J.
Samimy, M.
Soria, J.
and
Edgington-Mitchell, D.
2021.
Intermittent modal coupling in screeching underexpanded circular twin jets.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Zhang, Zhongyu
and
Wu, Xuesong
2022.
Nonlinear evolution and low-frequency acoustic radiation of ring-mode coherent structures on subsonic turbulent circular jets.
Journal of Fluid Mechanics,
Vol. 940,
Issue. ,
Zhang, Zhongyu
and
Wu, Xuesong
2023.
A unified theory for the envelope radiation of ring-mode coherent structures in the very-near-nozzle and developed regions of a circular jet.
Physics of Fluids,
Vol. 35,
Issue. 1,
Zhang, Zhongyu
and
Wu, Xuesong
2023.
Generation of sound waves by nonlinearly evolving ring-mode coherent structures on a turbulent subsonic circular jet: a comparative study of two mechanisms.
Acta Mechanica Sinica,
Vol. 39,
Issue. 3,
Webb, Nathan
Esfahani, Ata
Yoder, Samuel
Leahy, Ryan
and
Samimy, Mo
2023.
Empirical Closure Model for Coupling Mode Prediction in Supersonic Rectangular Twin Jets.
AIAA Journal,
Vol. 61,
Issue. 3,
p.
1238.
Zhang, Zhongyu
and
Wu, Xuesong
2023.
Nonlinear dynamics and acoustic radiation of coherent structures consisting of multiple ring–helical modes in the near-nozzle region of a subsonic turbulent circular jet.
Journal of Fluid Mechanics,
Vol. 973,
Issue. ,
Samimy, Mo
Webb, Nathan
Esfahani, Ata
and
Leahy, Ryan
2023.
Perturbation-based active flow control in overexpanded to underexpanded supersonic rectangular twin jets.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Li, Hongju
Liu, Ying
and
Liao, Haoran
2024.
Advances in Mechanism and Machine Science.
Vol. 149,
Issue. ,
p.
846.
Kiorpelidis, Ioannis
and
Bakas, Nikolaos A.
2025.
Parametric Instabilities in Time-Varying Compressible Linear Flows.
Fluids,
Vol. 10,
Issue. 1,
p.
18.
Zhang, Huan
and
Zheng, Xiaojing
2025.
Wavelet analysis of the coupling between turbulence, particles and electrostatics in dust storms.
Journal of Fluid Mechanics,
Vol. 1007,
Issue. ,
Hiler, Noah
Yarlagadda, Abhi
Katterle, Karli
Webb, Nathan J.
and
Samimy, Mo
2025.
Active Control of Coherent Structures in an Overexpanded Supersonic Rectangular Jet.
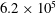 $6.2\times 10^{5}$ using plasma-based excitation of shear layer instabilities. The excitation frequency is varied to produce individual or periodic coherent ring vortices in the shear layer. First, two-point cross-correlations are used between the acoustic near field and far field in order to identify the dominant noise source region. The large-scale structure interactions are then investigated by stochastically estimating time-resolved velocity fields using time-resolved near-field pressure traces and non-time-resolved planar velocity snapshots (obtained by particle image velocimetry) by means of an artificial neural network. The estimated time-resolved velocity fields show multiple mergings of large-scale structures in the shear layer, and indicate that disintegration of coherent ring vortices is the dominant aeroacoustic source mechanism for the jet studied here. However, the merging of vortices in the initial shear layer is also identified as a non-trivial noise source mechanism.
$6.2\times 10^{5}$ using plasma-based excitation of shear layer instabilities. The excitation frequency is varied to produce individual or periodic coherent ring vortices in the shear layer. First, two-point cross-correlations are used between the acoustic near field and far field in order to identify the dominant noise source region. The large-scale structure interactions are then investigated by stochastically estimating time-resolved velocity fields using time-resolved near-field pressure traces and non-time-resolved planar velocity snapshots (obtained by particle image velocimetry) by means of an artificial neural network. The estimated time-resolved velocity fields show multiple mergings of large-scale structures in the shear layer, and indicate that disintegration of coherent ring vortices is the dominant aeroacoustic source mechanism for the jet studied here. However, the merging of vortices in the initial shear layer is also identified as a non-trivial noise source mechanism.


