1. Introduction
The study of propulsion mechanisms of small objects, organisms, swimmers or particles at low Reynolds numbers is a highly active area of current research (Nakata et al. Reference Nakata, Nagayama, Kitahata, Suematsu and Hasegawa2015; Zöttl & Stark Reference Zöttl and Stark2016; Suematsu & Nakata Reference Suematsu and Nakata2018; Michelin Reference Michelin2023). One mechanism whereby self-propulsion can be achieved is by the setting up of a Marangoni stress on an interface. This commonly involves an object, or ‘Marangoni surfer’ (Lauga & Davis Reference Lauga and Davis2011; Würger Reference Würger2014; Crowdy Reference Crowdy2020, Reference Crowdy2021a; Dietrich et al. Reference Dietrich, Jaensson, Buttinoni, Volpe and Isa2020), leveraging the benefit of its location at an interface between two fluids to release surfactants that cause a surface tension gradient, and a concomitant Marangoni stress, leading to locomotion. This phenomenon occurs in natural biological settings (Bush & Hu Reference Bush and Hu2006) and has also been exploited in synthetic situations (Nakata et al. Reference Nakata, Nagayama, Kitahata, Suematsu and Hasegawa2015; Suematsu & Nakata Reference Suematsu and Nakata2018). Several analytical models have been devised providing a theoretical understanding of this mode of locomotion in the viscous regime when surface diffusion of surfactant is dominant (Lauga & Davis Reference Lauga and Davis2011; Crowdy Reference Crowdy2020, Reference Crowdy2021a).
A closely related paradigm is the study of swimming droplets. A recent review (Maass et al. Reference Maass, Krüger, Herminghaus and Bahr2016) gives an overview of microswimmers based on liquid droplets where the propulsion mechanism does not require the presence of a separate interface or the imposition of some global external influence such as an imposed temperature gradient (Young, Goldstein & Block Reference Young, Goldstein and Block1959). It is also known that isotropic droplets, with no intrinsic asymmetry, can move spontaneously due to a nonlinear coupling between the transport of a solute with self-generated Marangoni flows. Michelin (Reference Michelin2023) has surveyed the recent results in this area. Typically, a droplet becomes active, and consequently self-propelling, due to a chemical reaction (Schmitt & Stark Reference Schmitt and Stark2013), micelle-induced solubilization or a phase transition (Maass et al. Reference Maass, Krüger, Herminghaus and Bahr2016).
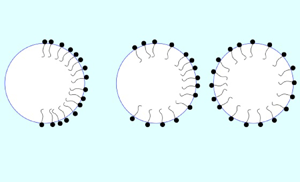
This paper presents an analytical study of unsteady bubble propulsion referred to here as viscous Marangoni migration by surfactant spreading. This mode of locomotion is illustrated in figure 1 where three time snapshots of a swimming bubble are shown. The model to be analysed is a two-dimensional inviscid bubble embedded in unbounded viscous fluid where some distribution of insoluble surfactant is set up on the bubble surface at some initial instant. Mathematically, this is an initial-value problem. How this initial distribution might be set up is not discussed here but if, as indicated in figure 1, there is an initial surplus of surfactant molecules on the right-hand side of the bubble the Marangoni stresses associated with its advective–diffusive spreading around the surface cause a Stokes flow in the surrounding viscous fluid and a net migration of the bubble to the right. This is because at zero Reynolds number the bubble must be free of net force and torque. The challenge is to determine the speed ![]() $U_B(t)$ of the bubble and its final net displacement
$U_B(t)$ of the bubble and its final net displacement ![]() $\Delta x$. Although any net locomotion relies on a breaking of symmetry in the initial surfactant distribution, the mechanism is intrinsically nonlinear because it depends on the advective–diffusive spreading of surfactant over the bubble surface. It is also inherently transient, perhaps more accurately described as bubble ‘hopping’ rather than ‘swimming’, because the migration is arrested as soon as the surfactant has spread to a uniform distribution. Further displacement can be envisaged by a repeat of this basic protocol, with more hops induced by a renewing of the initial left–right asymmetric surfactant distribution. Of course, such a strategy might be impeded by familiar short-lifetime challenges due to the loss of the surface tension gradient unless suitable surface reaction effects are also at work (Cheng et al. Reference Cheng, Zhang, Zhang, Wang and Shi2019). Such concerns are beyond the scope of this article.
$\Delta x$. Although any net locomotion relies on a breaking of symmetry in the initial surfactant distribution, the mechanism is intrinsically nonlinear because it depends on the advective–diffusive spreading of surfactant over the bubble surface. It is also inherently transient, perhaps more accurately described as bubble ‘hopping’ rather than ‘swimming’, because the migration is arrested as soon as the surfactant has spread to a uniform distribution. Further displacement can be envisaged by a repeat of this basic protocol, with more hops induced by a renewing of the initial left–right asymmetric surfactant distribution. Of course, such a strategy might be impeded by familiar short-lifetime challenges due to the loss of the surface tension gradient unless suitable surface reaction effects are also at work (Cheng et al. Reference Cheng, Zhang, Zhang, Wang and Shi2019). Such concerns are beyond the scope of this article.

Figure 1. Three snapshots of the unsteady migration of a single bubble due to an initial distribution of insoluble surfactant set up at ![]() $t=0$ which subsequently spreads around the surface. The motion is arrested when the distribution is uniform. The challenge is to determine the speed of the bubble
$t=0$ which subsequently spreads around the surface. The motion is arrested when the distribution is uniform. The challenge is to determine the speed of the bubble ![]() $U_B(t)$ and its net displacement
$U_B(t)$ and its net displacement ![]() $\Delta x$.
$\Delta x$.
The proposed basic mechanism is reminiscent of the strategic release of surfactant by insects, such as Microvelia, at interfaces to propel themselves along (Bush & Hu Reference Bush and Hu2006) although, in the case of a swimming bubble, it carries its own proprietary interface that travels with it, more akin to an insect's plastron. Tsemakh, Lavrenteva & Avinoam (Reference Tsemakh, Lavrenteva and Avinoam2004) have studied the swimming of a droplet in a viscous fluid due to Marangoni stresses set up at its surface due to the uniform secretion of a surface-active substance from a contained droplet placed off-centre inside the mother droplet. Mass transfer of this substance causes a surface Marangoni stress on the compound mother droplet that leads to net migration. Modern embodiments of similar ideas involving compound droplets of this kind but with different actuation mechanisms have been proposed by Ganesh et al. (Reference Ganesh, Koplik, Morris and Maldarelli2023).
Despite the nonlinear nature of the multiphysics problem in figure 1, the present study demonstrates that a two-dimensional model of such bubble migration can be solved in analytical form at any value of the surface Péclet number. The model makes a number of physically reasonable assumptions: that the Reynolds and capillary numbers are small, that a linear equation of state determines the surface tension as a function of the surfactant concentration and that the bubble dynamics is governed by nonlinear advection–diffusion of the insoluble surfactant on the bubble boundary leading to unsteady Marangoni stresses that determine a quasi-steady Stokes flow in the surrounding fluid.
Analytical solutions are possible because of a theoretical connection, elucidated here, between Marangoni dynamics and a complex form of the Burgers equation (Crowdy Reference Crowdy2021b,Reference Crowdyc). The latter is a nonlinear partial differential equation familiar to fluid dynamicists in its real version by virtue of its appearance in models of one-dimensional compressible gas dynamics (Whitham Reference Whitham1999). Indeed, the formulation here is a generalization, to the radial bubble geometry, of work by Crowdy (Reference Crowdy2021b,Reference Crowdyc) who showed that, under the same modelling assumptions just listed, insoluble surfactant dynamics on the surface of a half-plane region of viscous fluid can be described by a complex Burgers equation at arbitrary surface Péclet number. Although the mathematical details are different, the main theoretical ramifications of that prior work carry over to the bubble geometry. Arguably the most significant implication is that the nonlinear swimming bubble problem of interest here can be linearized at any non-zero surface Péclet number by a complex-valued variant of the classical Cole–Hopf transformation (Whitham Reference Whitham1999; Crowdy Reference Crowdy2021b,Reference Crowdyc).
Although the model is limited in its physical relevance in being two-dimensional, its amenability to closed-form analytical solution renders it valuable in exemplifying fundamental physical mechanisms in mathematical form. Several theoretical studies on two-dimensional swimming droplets have similarly been of value in providing insights into basic effects (Hu et al. Reference Hu, Lin, Rafai and Misbah2019; Li Reference Li2022).
2. Bubble migration by surfactant spreading
A circular, two-dimensional, inviscid, incompressible bubble of radius ![]() ${\mathcal {R}}$ is initially centred on the
${\mathcal {R}}$ is initially centred on the ![]() $x$ axis in an
$x$ axis in an ![]() $(x,y)$ plane and is surrounded by unbounded fluid of viscosity
$(x,y)$ plane and is surrounded by unbounded fluid of viscosity ![]() $\mu$. The bubble has constant pressure
$\mu$. The bubble has constant pressure ![]() $p_B$. It is assumed that, at
$p_B$. It is assumed that, at ![]() $t=0$, there is some mechanism that instantaneously sets up an initial concentration
$t=0$, there is some mechanism that instantaneously sets up an initial concentration ![]() $\varGamma (s,0) = \varGamma _0(s)$ of surfactant on the bubble boundary, taken to be symmetric about the diameter along the
$\varGamma (s,0) = \varGamma _0(s)$ of surfactant on the bubble boundary, taken to be symmetric about the diameter along the ![]() $x$ axis, where
$x$ axis, where ![]() $s$ is arclength in the boundary tangent direction taken clockwise around the bubble boundary. The assumption of symmetry about the
$s$ is arclength in the boundary tangent direction taken clockwise around the bubble boundary. The assumption of symmetry about the ![]() $x$ axis is not necessary, but it simplifies the analysis and statement of the main results. All that follows can be generalized if this assumption is relaxed.
$x$ axis is not necessary, but it simplifies the analysis and statement of the main results. All that follows can be generalized if this assumption is relaxed.
The surfactant is assumed to be insoluble to the bulk fluid but can be advected around the bubble surface and diffuses along it with surface diffusion coefficient ![]() $D_s$. The surfactant affects the local surface tension
$D_s$. The surfactant affects the local surface tension ![]() $\sigma (s,t)$ according to the linear equation of state
$\sigma (s,t)$ according to the linear equation of state
where ![]() $\sigma _c$ is the clean-flow surface tension and
$\sigma _c$ is the clean-flow surface tension and ![]() $\beta = RT$, where
$\beta = RT$, where ![]() $T$ is absolute temperature, assumed to be constant, and
$T$ is absolute temperature, assumed to be constant, and ![]() $R$ is the gas constant. A capillary number, to be introduced later, based on the clean-flow surface tension
$R$ is the gas constant. A capillary number, to be introduced later, based on the clean-flow surface tension ![]() $\sigma _c$ is assumed small so that the bubble can be taken to remain circular and undeformed at leading order. An initial concentration of surfactant such as that shown in figure 1 will spread around the bubble causing a time-dependent Marangoni stress on its boundary. As a result, the bubble is expected to move in the
$\sigma _c$ is assumed small so that the bubble can be taken to remain circular and undeformed at leading order. An initial concentration of surfactant such as that shown in figure 1 will spread around the bubble causing a time-dependent Marangoni stress on its boundary. As a result, the bubble is expected to move in the ![]() $x$ direction with some time-dependent speed
$x$ direction with some time-dependent speed ![]() $U_B(t)$. Since the motion is arrested when the surfactant distribution has spread out to become uniform, the bubble will ultimately, at large times, be displaced by some finite distance
$U_B(t)$. Since the motion is arrested when the surfactant distribution has spread out to become uniform, the bubble will ultimately, at large times, be displaced by some finite distance ![]() $\Delta x$ from its starting point. The aim of this paper is to determine the bubble speed
$\Delta x$ from its starting point. The aim of this paper is to determine the bubble speed ![]() $U_B(t)$ and total bubble displacement
$U_B(t)$ and total bubble displacement ![]() $\Delta x$ as a function of the initial surfactant concentration profile.
$\Delta x$ as a function of the initial surfactant concentration profile.
It is natural to move to a bubble-fixed frame of reference co-travelling with the bubble at each instant with speed ![]() $U_B(t)$ that is unknown a priori. Assuming a Reynolds number based on
$U_B(t)$ that is unknown a priori. Assuming a Reynolds number based on ![]() $U_B$,
$U_B$, ![]() ${\mathcal {R}}$ and
${\mathcal {R}}$ and ![]() $\mu$ is sufficiently small, the fluid velocity
$\mu$ is sufficiently small, the fluid velocity ![]() $\boldsymbol {u}=(u,v)$ outside the bubble in this frame can be taken to satisfy the incompressible quasi-steady Stokes equations
$\boldsymbol {u}=(u,v)$ outside the bubble in this frame can be taken to satisfy the incompressible quasi-steady Stokes equations
where ![]() $p(x,y,t)$ is the fluid pressure. The unit tangent
$p(x,y,t)$ is the fluid pressure. The unit tangent ![]() $\boldsymbol {t}$ and normal
$\boldsymbol {t}$ and normal ![]() $\boldsymbol {n}$ vectors are indicated in figure 2; note that
$\boldsymbol {n}$ vectors are indicated in figure 2; note that ![]() $\boldsymbol {t}$ is directed clockwise around the boundary while
$\boldsymbol {t}$ is directed clockwise around the boundary while ![]() $\boldsymbol {n}$ points into the viscous fluid from the bubble. A kinematic condition on the bubble boundary is
$\boldsymbol {n}$ points into the viscous fluid from the bubble. A kinematic condition on the bubble boundary is
This states that the boundary must be a streamline in the co-travelling frame. The stress balance on the bubble boundary is
where ![]() $n_i$ and
$n_i$ and ![]() $t_i$ denote the
$t_i$ denote the ![]() $i$th components of
$i$th components of ![]() $\boldsymbol {n}$ and
$\boldsymbol {n}$ and ![]() $\boldsymbol {t}$, respectively, and
$\boldsymbol {t}$, respectively, and ![]() $e_{ij}$ is the usual fluid rate-of-strain tensor. The second term on the right-hand side of (2.4) represents the Marangoni stress caused by the varying surface tension. The surface tension
$e_{ij}$ is the usual fluid rate-of-strain tensor. The second term on the right-hand side of (2.4) represents the Marangoni stress caused by the varying surface tension. The surface tension ![]() $\sigma (s,t)$ is given by (2.1) where
$\sigma (s,t)$ is given by (2.1) where ![]() $\varGamma (s,t)$ satisfies the surfactant evolution equation which, in a frame of reference co-moving with the fixed-shape bubble, is (Wong, Rumschitzki & Maldarelli Reference Wong, Rumschitzki and Maldarelli1996)
$\varGamma (s,t)$ satisfies the surfactant evolution equation which, in a frame of reference co-moving with the fixed-shape bubble, is (Wong, Rumschitzki & Maldarelli Reference Wong, Rumschitzki and Maldarelli1996)
where ![]() $U(s,t)$ is the surface slip velocity in the tangential direction. On integrating (2.5) around the entire bubble boundary it follows that the average surfactant concentration over the interface, denoted by
$U(s,t)$ is the surface slip velocity in the tangential direction. On integrating (2.5) around the entire bubble boundary it follows that the average surfactant concentration over the interface, denoted by ![]() $\langle {\varGamma _0} \rangle$, is a constant of the motion, namely
$\langle {\varGamma _0} \rangle$, is a constant of the motion, namely
where it is convenient to take ![]() $s=0$ to correspond to the front of the bubble at
$s=0$ to correspond to the front of the bubble at ![]() $x={\mathcal {R}}$ on the positive
$x={\mathcal {R}}$ on the positive ![]() $x$ axis. The condition on the fluid velocity in the far field is
$x$ axis. The condition on the fluid velocity in the far field is
where the condition that the bubble is free of net force determines ![]() $U_B(t)$. The assumed reflectional symmetry of the initial surfactant concentration about the
$U_B(t)$. The assumed reflectional symmetry of the initial surfactant concentration about the ![]() $x$ axis through the bubble centre is expected to be dynamically preserved and ensures zero net torque on it.
$x$ axis through the bubble centre is expected to be dynamically preserved and ensures zero net torque on it.
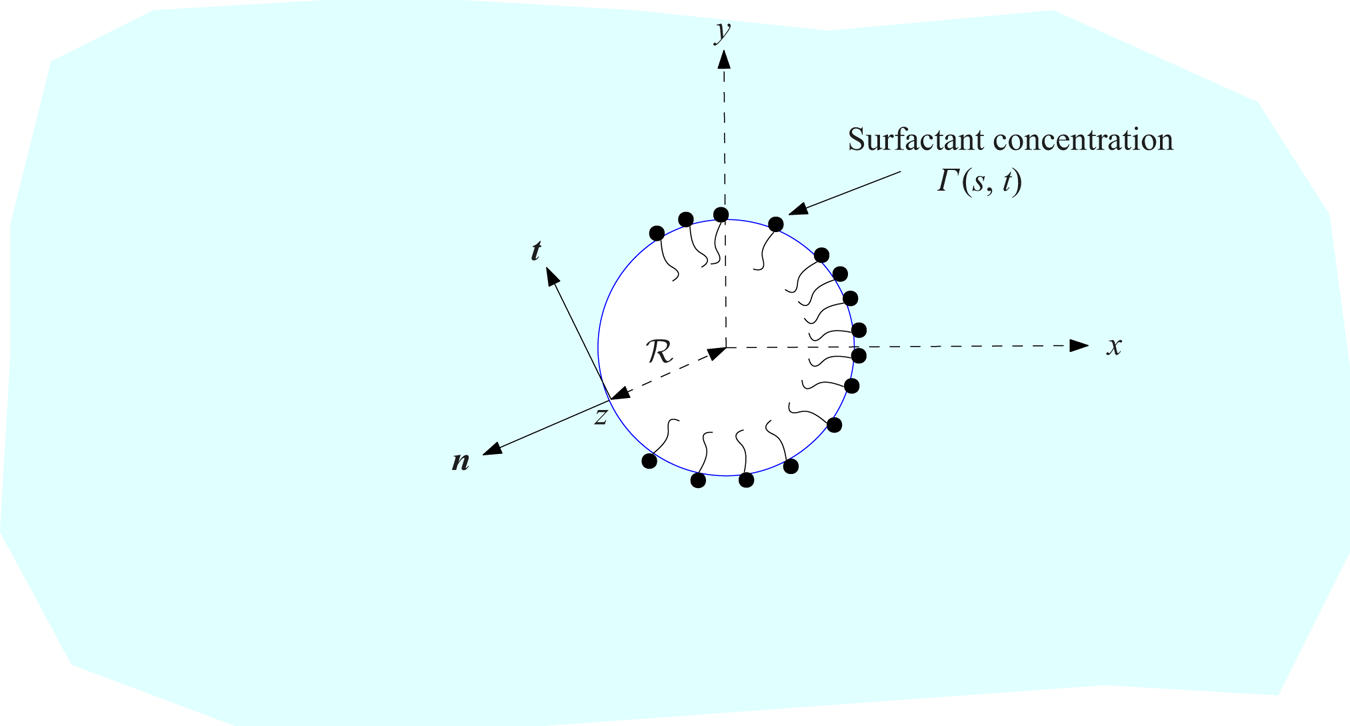
Figure 2. A circular bubble of radius ![]() ${\mathcal {R}}$ in a complex
${\mathcal {R}}$ in a complex ![]() $z=x+{\rm i} y$ plane. If
$z=x+{\rm i} y$ plane. If ![]() $z$ is a point on the bubble boundary the complex analogue of the unit normal vector
$z$ is a point on the bubble boundary the complex analogue of the unit normal vector ![]() $\boldsymbol {n}$ is
$\boldsymbol {n}$ is ![]() $z/{\mathcal {R}}$ and the complex analogue of the unit tangent vector
$z/{\mathcal {R}}$ and the complex analogue of the unit tangent vector ![]() $\boldsymbol {t}$ is
$\boldsymbol {t}$ is ![]() $-{\rm i}(z/{\mathcal {R}})$. The arclength
$-{\rm i}(z/{\mathcal {R}})$. The arclength ![]() $s$ increases in the direction of
$s$ increases in the direction of ![]() $\boldsymbol {t}$.
$\boldsymbol {t}$.
Unless surface diffusion of surfactant is dominant, this multiphysics problem constitutes a nonlinear system where the surface advection–diffusion of the surfactant determines the instantaneous Stokes flow in the bulk which, in turn, feeds back to affect the surfactant advection on the moving bubble.
3. Complex variable formulation
The flow generated by the surfactant evolution will be found using a complex variable formulation of two-dimensional, quasi-steady Stokes flow of which an appendix of Crowdy (Reference Crowdy2020) gives a brief derivation. On taking the curl of the Stokes equations (2.2) and introducing a streamfunction ![]() $\psi$ associated with the incompressible two-dimensional flow,
$\psi$ associated with the incompressible two-dimensional flow,
it can be shown that ![]() $\psi$ satisfies the biharmonic equation in the fluid region, namely
$\psi$ satisfies the biharmonic equation in the fluid region, namely
On letting ![]() $z=x +{\rm i}y$ this partial differential equation can be written as
$z=x +{\rm i}y$ this partial differential equation can be written as
which can be integrated (Crowdy Reference Crowdy2020) leading to a general representation of a real-valued biharmonic streamfunction given by
where ![]() ${\rm Im}[\cdot ]$ denotes the imaginary part of the complex quantity in square brackets and
${\rm Im}[\cdot ]$ denotes the imaginary part of the complex quantity in square brackets and ![]() $f(z,t)$ and
$f(z,t)$ and ![]() $g(z,t)$ are complex potentials, also known as Goursat functions. In general, all singularities of these analytic functions must be inside the bubble, or at infinity, and not in the viscous fluid. Moreover, a logarithmic singularity of
$g(z,t)$ are complex potentials, also known as Goursat functions. In general, all singularities of these analytic functions must be inside the bubble, or at infinity, and not in the viscous fluid. Moreover, a logarithmic singularity of ![]() $f(z,t)$ inside the bubble can be identified with a Stokeslet singularity implying a non-zero net force on the bubble while a logarithmic singularity of
$f(z,t)$ inside the bubble can be identified with a Stokeslet singularity implying a non-zero net force on the bubble while a logarithmic singularity of ![]() $g(z,t)$ inside the bubble can be identified with a rotlet singularity implying a non-zero net torque on it. Since, in the present problem, the bubble is free of net force and torque, both
$g(z,t)$ inside the bubble can be identified with a rotlet singularity implying a non-zero net torque on it. Since, in the present problem, the bubble is free of net force and torque, both ![]() $f(z,t)$ and
$f(z,t)$ and ![]() $g(z,t)$ will be analytic and single-valued in the viscous fluid region. This is explained in more detail in what follows.
$g(z,t)$ will be analytic and single-valued in the viscous fluid region. This is explained in more detail in what follows.
It can be shown (Crowdy Reference Crowdy2020) that ![]() $p(x,y,t)$, the vorticity
$p(x,y,t)$, the vorticity ![]() $\omega = -\nabla ^2 \psi$ and the fluid rate-of-strain tensor
$\omega = -\nabla ^2 \psi$ and the fluid rate-of-strain tensor ![]() $e_{ij}$ are related to
$e_{ij}$ are related to ![]() $f(z,t)$ and
$f(z,t)$ and ![]() $g(z,t)$ through the relations
$g(z,t)$ through the relations
 \begin{equation} \left.\begin{array}{@{}c@{}} 4f'(z,t) = \dfrac{p }{\mu} - {\rm i} \omega, \quad u - {\rm i} v ={-} \overline{f(z,t)} + \bar{z} {f'(z,t)} + {g'(z,t)} , \\ e_{11} + {\rm i} e_{12} = z \overline{f''(z,t)} +\overline{g''(z,t)}, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} 4f'(z,t) = \dfrac{p }{\mu} - {\rm i} \omega, \quad u - {\rm i} v ={-} \overline{f(z,t)} + \bar{z} {f'(z,t)} + {g'(z,t)} , \\ e_{11} + {\rm i} e_{12} = z \overline{f''(z,t)} +\overline{g''(z,t)}, \end{array}\right\} \end{equation}
where overbars denote complex conjugation and the prime notation denotes partial differentiation with respect to ![]() $z$. There is an additive degree of freedom in the choice of
$z$. There is an additive degree of freedom in the choice of ![]() $f(z,t)$ and
$f(z,t)$ and ![]() $g'(z,t)$ since if
$g'(z,t)$ since if ![]() $f(z,t)$ is changed to
$f(z,t)$ is changed to ![]() $f(z,t) + c(t)$ and
$f(z,t) + c(t)$ and ![]() $g'(z,t)$ is changed to
$g'(z,t)$ is changed to ![]() $g'(z,t) + \overline {c(t)}$, where
$g'(z,t) + \overline {c(t)}$, where ![]() $c(t)$ is a complex function of time, then the complex velocity field
$c(t)$ is a complex function of time, then the complex velocity field ![]() $u-\textrm {i}v$ given in (3.5) is unaltered. This degree of freedom is eliminated shortly.
$u-\textrm {i}v$ given in (3.5) is unaltered. This degree of freedom is eliminated shortly.
The complex form of the fluid stress at the boundary, or ![]() $-p n_i + 2 \mu e_{ij}n_j$, is (Crowdy Reference Crowdy2020)
$-p n_i + 2 \mu e_{ij}n_j$, is (Crowdy Reference Crowdy2020)
Since there is no net force on the bubble then integration of the fluid stress (3.6) with respect to arclength around its boundary must give zero. This means that ![]() $H(z,\bar {z},t)$ must be single-valued around the bubble. The single-valuedness of
$H(z,\bar {z},t)$ must be single-valued around the bubble. The single-valuedness of ![]() $f(z,t$) around the bubble then follows on noticing, from (3.5) and (3.6), that
$f(z,t$) around the bubble then follows on noticing, from (3.5) and (3.6), that ![]() $H(z,\bar {z},t) = 2f(z,t)+ (u+\textrm {i}v)$ and bearing in mind that
$H(z,\bar {z},t) = 2f(z,t)+ (u+\textrm {i}v)$ and bearing in mind that ![]() $u+\textrm {i} v$ is necessarily single-valued around the bubble.
$u+\textrm {i} v$ is necessarily single-valued around the bubble.
On rearrangement, the stress condition (2.4) on the bubble boundary can be written as
which will now be written in complex form. For this, note that the complex form of the unit tangent vector is
and the complex form of the unit normal vector is
Consequently, the complex variable statement of (3.7) is
 \begin{align} - 2 \mu {\rm i} \frac{\partial H }{\partial s} &= \frac{\sigma }{{\mathcal{R}}} {\rm i} \frac{{\rm d}z }{{\rm d}s} - \frac{\partial \sigma }{\partial s} \frac{{\rm d}z }{{\rm d}s} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s} = \frac{{\rm i} \sigma }{{\mathcal{R}}} \frac{{\rm d}z }{{\rm d}s} + \frac{\partial \sigma }{\partial s} \frac{{\rm i} z }{{\mathcal{R}}} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s}\nonumber\\ & = \frac{{\rm i} }{{\mathcal{R}}} \frac{\partial (\sigma z) }{\partial s} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s}, \end{align}
\begin{align} - 2 \mu {\rm i} \frac{\partial H }{\partial s} &= \frac{\sigma }{{\mathcal{R}}} {\rm i} \frac{{\rm d}z }{{\rm d}s} - \frac{\partial \sigma }{\partial s} \frac{{\rm d}z }{{\rm d}s} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s} = \frac{{\rm i} \sigma }{{\mathcal{R}}} \frac{{\rm d}z }{{\rm d}s} + \frac{\partial \sigma }{\partial s} \frac{{\rm i} z }{{\mathcal{R}}} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s}\nonumber\\ & = \frac{{\rm i} }{{\mathcal{R}}} \frac{\partial (\sigma z) }{\partial s} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s}, \end{align}
where (3.6), (3.8) and (3.9) have been used. This can be integrated with respect to ![]() $s$ to give
$s$ to give
where an additive function of time has been set to zero without loss of generality by exploiting the aforementioned additive degree of freedom in the choice of ![]() $f(z,t)$ and
$f(z,t)$ and ![]() $g'(z,t)$. On use of the equation of state (2.1), (3.11) implies that
$g'(z,t)$. On use of the equation of state (2.1), (3.11) implies that
The next step is to introduce the decompositions
where ![]() $p_H$ is a real constant and
$p_H$ is a real constant and ![]() $\hat f(z,t)$ is analytic and single-valued in the fluid region
$\hat f(z,t)$ is analytic and single-valued in the fluid region ![]() $|z| > {\mathcal {R}}$ except for a simple pole at infinity, i.e.
$|z| > {\mathcal {R}}$ except for a simple pole at infinity, i.e.
as ![]() $|z| \to \infty$ where
$|z| \to \infty$ where ![]() $\hat p(t)$ is real-valued. The first term of
$\hat p(t)$ is real-valued. The first term of ![]() $f(z,t)$ in (3.13) encodes the hydrostatic pressure
$f(z,t)$ in (3.13) encodes the hydrostatic pressure ![]() $p_H$ of a clean bubble and the additional term
$p_H$ of a clean bubble and the additional term ![]() $\hat f(z,t)$ will describe the quasi-steady Stokes flow generated by the surfactant effects. The quantity
$\hat f(z,t)$ will describe the quasi-steady Stokes flow generated by the surfactant effects. The quantity ![]() $\hat p(t)$ represents the modification to the far-field fluid pressure due to the presence of the surfactant and it is easy to check from (3.5) and (2.7) that the constant term in the far-field asymptotics (3.14) is the bubble speed
$\hat p(t)$ represents the modification to the far-field fluid pressure due to the presence of the surfactant and it is easy to check from (3.5) and (2.7) that the constant term in the far-field asymptotics (3.14) is the bubble speed ![]() $U_B(t)$. An important feature of the choice (3.13) is that it satisfies the streamline condition (2.3) on the bubble surface for any
$U_B(t)$. An important feature of the choice (3.13) is that it satisfies the streamline condition (2.3) on the bubble surface for any ![]() $\hat f(z,t)$. This is because, on
$\hat f(z,t)$. This is because, on ![]() $|z| = {\mathcal {R}}$,
$|z| = {\mathcal {R}}$,
 \begin{equation} \psi(z, \bar{z}, t) = {\rm Im}[\bar{z} f(z,t) + g(z,t)] = {\rm Im} \left [ \bar{z} \left (\frac{p_H }{4 \mu} z + \hat f(z,t) \right ) - \frac{{\mathcal{R}}^2 \hat f(z,t) }{z} \right ] = 0, \end{equation}
\begin{equation} \psi(z, \bar{z}, t) = {\rm Im}[\bar{z} f(z,t) + g(z,t)] = {\rm Im} \left [ \bar{z} \left (\frac{p_H }{4 \mu} z + \hat f(z,t) \right ) - \frac{{\mathcal{R}}^2 \hat f(z,t) }{z} \right ] = 0, \end{equation}
where the fact that ![]() $\bar {z}={\mathcal {R}}^2/z$ on the bubble boundary has been used. The bubble boundary is therefore a streamline.
$\bar {z}={\mathcal {R}}^2/z$ on the bubble boundary has been used. The bubble boundary is therefore a streamline.
On substitution of the decompositions (3.13) into the definition of ![]() $H(z, \bar {z}, t)$ given in (3.6) it follows that, on
$H(z, \bar {z}, t)$ given in (3.6) it follows that, on ![]() $|z|= {\mathcal {R}}$,
$|z|= {\mathcal {R}}$,
 \begin{align} H(z, \bar{z}, t) &= \frac{p_H }{4 \mu} z + \hat f(z,t) + \frac{p_H }{4 \mu} z + z \overline{\hat f'(z,t)} - {\mathcal{R}}^2 \overline{\left (\frac{\hat f'(z,t) }{z} \right )} + {\mathcal{R}}^2\overline{\left (\frac{\hat f(z,t) }{z^2}\right ) }\nonumber\\ &= \frac{p_H }{2 \mu} z + \hat f(z,t) +{\mathcal{R}}^2 \overline{\left (\frac{\hat f(z,t) }{z^2}\right ) }, \end{align}
\begin{align} H(z, \bar{z}, t) &= \frac{p_H }{4 \mu} z + \hat f(z,t) + \frac{p_H }{4 \mu} z + z \overline{\hat f'(z,t)} - {\mathcal{R}}^2 \overline{\left (\frac{\hat f'(z,t) }{z} \right )} + {\mathcal{R}}^2\overline{\left (\frac{\hat f(z,t) }{z^2}\right ) }\nonumber\\ &= \frac{p_H }{2 \mu} z + \hat f(z,t) +{\mathcal{R}}^2 \overline{\left (\frac{\hat f(z,t) }{z^2}\right ) }, \end{align}
where the fact that ![]() ${z} = {\mathcal {R}}^2/\bar {z}$ on
${z} = {\mathcal {R}}^2/\bar {z}$ on ![]() $|z|= {\mathcal {R}}$ has been used. On division by
$|z|= {\mathcal {R}}$ has been used. On division by ![]() $z$, this becomes
$z$, this becomes
 \begin{equation} \frac{H(z, \bar{z},t) }{z} = \frac{p_H }{2\mu} + 2 {\rm Re} \left [ \frac{\hat f(z,t) }{z} \right ] = \frac{p_H }{2\mu} + {\rm Re}[h(z,t)], \end{equation}
\begin{equation} \frac{H(z, \bar{z},t) }{z} = \frac{p_H }{2\mu} + 2 {\rm Re} \left [ \frac{\hat f(z,t) }{z} \right ] = \frac{p_H }{2\mu} + {\rm Re}[h(z,t)], \end{equation}where
The function ![]() $h(z,t)$ is analytic and single-valued in the fluid region, properties it inherits from
$h(z,t)$ is analytic and single-valued in the fluid region, properties it inherits from ![]() $\hat f(z,t)$ in view of its definition (3.18) and the far-field behaviour (3.14). Two expressions for
$\hat f(z,t)$ in view of its definition (3.18) and the far-field behaviour (3.14). Two expressions for ![]() $H/z$ have now been derived in (3.12) and (3.17). Setting them equal leads to
$H/z$ have now been derived in (3.12) and (3.17). Setting them equal leads to
It turns out that the boundary slip velocity ![]() $U(s,t)$ can also be conveniently expressed in terms of
$U(s,t)$ can also be conveniently expressed in terms of ![]() $h(z,t)$. To see this, note that on
$h(z,t)$. To see this, note that on ![]() $|z|= {\mathcal {R}}$, where
$|z|= {\mathcal {R}}$, where ![]() $\bar {z} = {\mathcal {R}}^2/{z}$, it follows from (3.5) and (3.13) that
$\bar {z} = {\mathcal {R}}^2/{z}$, it follows from (3.5) and (3.13) that
Using the fact that if ![]() $a=a_x+\textrm {i} a_y$ and
$a=a_x+\textrm {i} a_y$ and ![]() $b=b_x+\textrm {i}b_y$ are the complex analogues of the vectors
$b=b_x+\textrm {i}b_y$ are the complex analogues of the vectors ![]() $\boldsymbol {a}=(a_x, a_y)$ and
$\boldsymbol {a}=(a_x, a_y)$ and ![]() $\boldsymbol {b}=(b_x, b_y)$ then the complex analogue of the dot product
$\boldsymbol {b}=(b_x, b_y)$ then the complex analogue of the dot product ![]() $\boldsymbol {a}\boldsymbol {\cdot }\boldsymbol {b}$ is
$\boldsymbol {a}\boldsymbol {\cdot }\boldsymbol {b}$ is ![]() $\textrm {Re}[a \bar {b}]$ then the boundary slip velocity
$\textrm {Re}[a \bar {b}]$ then the boundary slip velocity ![]() $U(s,t)$ can be written, in complex form, as
$U(s,t)$ can be written, in complex form, as
 \begin{align} U(s,t) &= \boldsymbol{t}\boldsymbol{\cdot} \boldsymbol{u} = {\rm Re} \left [ - \frac{{\rm i} z }{{\mathcal{R}}} \left (-\overline{\hat f(z,t)} + {\mathcal{R}}^2 \frac{\hat f(z,t) }{z^2} \right ) \right ]\nonumber\\ &= {\rm Re} \left [ - {{\rm i} {\mathcal{R}}} \left (\frac{\hat f(z,t) }{z} - \overline{ \left (\frac{\hat f(z,t) }{z} \right )} \right ) \right ] = {\mathcal{R}} \,{\rm Im} \left [ \frac{\hat f(z,t) }{z} - \overline{ \left (\frac{\hat f(z,t) }{z} \right )} \right ], \end{align}
\begin{align} U(s,t) &= \boldsymbol{t}\boldsymbol{\cdot} \boldsymbol{u} = {\rm Re} \left [ - \frac{{\rm i} z }{{\mathcal{R}}} \left (-\overline{\hat f(z,t)} + {\mathcal{R}}^2 \frac{\hat f(z,t) }{z^2} \right ) \right ]\nonumber\\ &= {\rm Re} \left [ - {{\rm i} {\mathcal{R}}} \left (\frac{\hat f(z,t) }{z} - \overline{ \left (\frac{\hat f(z,t) }{z} \right )} \right ) \right ] = {\mathcal{R}} \,{\rm Im} \left [ \frac{\hat f(z,t) }{z} - \overline{ \left (\frac{\hat f(z,t) }{z} \right )} \right ], \end{align}where the complex form of the unit tangent (3.8) has been used. Therefore, on the boundary,
 \begin{equation} \frac{U(s,t) }{{\mathcal{R}}} = 2 \,{\rm Im} \left [ \frac{\hat f(z,t) }{z} \right ] = {\rm Im}[h(z,t)]. \end{equation}
\begin{equation} \frac{U(s,t) }{{\mathcal{R}}} = 2 \,{\rm Im} \left [ \frac{\hat f(z,t) }{z} \right ] = {\rm Im}[h(z,t)]. \end{equation}4. A complex partial differential equation of Burgers type
A velocity scale associated with the presence of the surfactant is
It is natural to non-dimensionalize lengths using the bubble radius ![]() ${\mathcal {R}}$, surfactant concentrations using
${\mathcal {R}}$, surfactant concentrations using ![]() $\langle \varGamma _0 \rangle$, velocities induced by the presence of the surfactant using
$\langle \varGamma _0 \rangle$, velocities induced by the presence of the surfactant using ![]() $U_0$ and time using
$U_0$ and time using ![]() ${\mathcal {R}}/U_0$. The hydrostatic pressure
${\mathcal {R}}/U_0$. The hydrostatic pressure ![]() $p_H$ and bubble pressure
$p_H$ and bubble pressure ![]() $p_B$ are non-dimensionalized using
$p_B$ are non-dimensionalized using ![]() $\sigma _c/{\mathcal {R}}$. The bubble boundary is now
$\sigma _c/{\mathcal {R}}$. The bubble boundary is now ![]() $|z|=1$ and it can be parametrized by
$|z|=1$ and it can be parametrized by ![]() $z=\textrm {e}^{-\textrm {i}s}$, where
$z=\textrm {e}^{-\textrm {i}s}$, where ![]() $s$ is the non-dimensional arclength. Noting that
$s$ is the non-dimensional arclength. Noting that ![]() $\hat f(z,t)$ has the dimension of a velocity, the non-dimensional version of (3.22) is
$\hat f(z,t)$ has the dimension of a velocity, the non-dimensional version of (3.22) is
where a quantity decorated with a tilde denotes its non-dimensional counterpart. Equation (3.19) becomes
or
if (4.1) is used. The capillary number, which was mentioned earlier, can now be introduced as
and taken to be small, i.e. ![]() $Ca \ll 1$. In terms of it, (4.4) becomes
$Ca \ll 1$. In terms of it, (4.4) becomes
Hence, at leading order, the Laplace–Young balance holds:
where the constant right-hand side encodes the constant curvature of the interface and, at first order in ![]() $Ca$, it follows from (4.6) that
$Ca$, it follows from (4.6) that
A consequence of (4.8) is that the average of the real part of ![]() $\tilde h(z,t)$ around the bubble boundary is unity since, by the choice of scaling, this is the value of the surface average of the non-dimensionalized surfactant concentration.
$\tilde h(z,t)$ around the bubble boundary is unity since, by the choice of scaling, this is the value of the surface average of the non-dimensionalized surfactant concentration.
Henceforth, the tildes on any non-dimensionalized quantities will be dropped. Together, (4.2) and (4.8) imply that
Equation (4.9) is important: it is the radial geometry analogue of a similar relation obtained in Crowdy (Reference Crowdy2021b,Reference Crowdyc) for a half-plane geometry for which the boundary of the viscous fluid region is an infinite straight line. A subsequent trivial, but important, observation is that
where (4.9) has simply been squared.
It is expedient now to return to the surfactant evolution equation (2.5) which, on use of (4.9) and (4.10), takes the non-dimensionalized form
where the surface Péclet number is
By the chain rule, since ![]() $z=\textrm {e}^{-\textrm {i}s}$ on the bubble boundary,
$z=\textrm {e}^{-\textrm {i}s}$ on the bubble boundary,
hence (4.11) can be written as
The quantity in square brackets in (4.14) is analytic and single-valued in ![]() $|z| > 1$ except possibly at infinity. However, the problem under current consideration is such that
$|z| > 1$ except possibly at infinity. However, the problem under current consideration is such that
where the first term in the far-field behaviour of ![]() $h(z,t)$ ensures that the surface average of the real part of
$h(z,t)$ ensures that the surface average of the real part of ![]() $h(z,t)$ is unity, a requirement just noted. This is because, being analytic and single-valued in
$h(z,t)$ is unity, a requirement just noted. This is because, being analytic and single-valued in ![]() $|z| > 1$,
$|z| > 1$, ![]() $h(z,t)$ has a convergent Laurent series there and only the constant term in this series will contribute to the average of
$h(z,t)$ has a convergent Laurent series there and only the constant term in this series will contribute to the average of ![]() $\textrm {Re}[h(z,t)]$ around the bubble boundary. The behaviour (4.15) means that the function in square brackets in (4.14) is analytic and single-valued for
$\textrm {Re}[h(z,t)]$ around the bubble boundary. The behaviour (4.15) means that the function in square brackets in (4.14) is analytic and single-valued for ![]() $|z| > 1$, including as
$|z| > 1$, including as ![]() $|z| \to \infty$ where it decays like
$|z| \to \infty$ where it decays like ![]() $1/z$. Given that, according to (4.14), this function also has vanishing real part on
$1/z$. Given that, according to (4.14), this function also has vanishing real part on ![]() $|z|=1$ it follows by analytic continuation off the boundary circle
$|z|=1$ it follows by analytic continuation off the boundary circle ![]() $|z|=1$ that
$|z|=1$ that
everywhere in ![]() $|z| > 1$.
$|z| > 1$.
Equation (4.16) is a key result of this paper. It is the radial geometry analogue of a complex Burgers equation obtained for the half-plane geometry in Crowdy (Reference Crowdy2021b,Reference Crowdyc) where, in that case, the relevant lower-analytic function ![]() $h(z,t)$ had a different functional connection to
$h(z,t)$ had a different functional connection to ![]() $f(z,t)$. The reduction of the swimming bubble problem to this complex partial differential equation of Burgers type (4.16) has significant theoretical ramifications to be explored next.
$f(z,t)$. The reduction of the swimming bubble problem to this complex partial differential equation of Burgers type (4.16) has significant theoretical ramifications to be explored next.
5. Bubble migration as  $Pe_s \to \infty$: method of characteristics
$Pe_s \to \infty$: method of characteristics
The case of infinite surface Péclet number is studied first. On taking the limit ![]() $Pe_s \to \infty$, implying negligible surface diffusion, the governing equation (4.16) reduces to
$Pe_s \to \infty$, implying negligible surface diffusion, the governing equation (4.16) reduces to
This can be solved by a complex method of characteristics in the spirit of similar calculations carried out for the half-plane geometry in Crowdy (Reference Crowdy2021b,Reference Crowdyc). Equation (5.1) implies that
on complex characteristics defined by
The variable ![]() $Z$ can be thought of as labelling the characteristics; the function
$Z$ can be thought of as labelling the characteristics; the function ![]() $H(Z)$ is determined by initial conditions:
$H(Z)$ is determined by initial conditions: ![]() $h(z,0)=h(Z,0) = H(Z)$. Equations (5.2) and (5.3) together imply that
$h(z,0)=h(Z,0) = H(Z)$. Equations (5.2) and (5.3) together imply that
implying
after an integration is performed and initial conditions imposed. An implicit form of the general solution to the problem, parametrized by the complex variable ![]() $Z$, is therefore
$Z$, is therefore
For a given ![]() $H(Z)$ formulas (5.6) give an implicit parametric representation of the solution for arbitrary initial data from which the time-evolving solution can easily be extracted numerically by a nonlinear solver. The swimming bubble problem at infinite surface Péclet number is therefore integrable in this sense.
$H(Z)$ formulas (5.6) give an implicit parametric representation of the solution for arbitrary initial data from which the time-evolving solution can easily be extracted numerically by a nonlinear solver. The swimming bubble problem at infinite surface Péclet number is therefore integrable in this sense.
The next subsection showcases a particular class of initial conditions for which this implicit solution (5.6) can be rendered explicit in terms of the Lambert W-function (Olver et al. Reference Olver, Daalhuis, Lozier, Schneider, Boisvert, Clark, Mille, Saunders, Cohl and McClain2020).
5.1. A special class of initial conditions
Suppose that
where ![]() $B$ is a real constant. It follows that, on the bubble surface,
$B$ is a real constant. It follows that, on the bubble surface,
so the corresponding initial surfactant distribution can be read off as
This is non-negative everywhere on the bubble boundary because of the stipulation that ![]() $|B| \le 1$. If
$|B| \le 1$. If ![]() $0 < B \le 1$ the maximum value
$0 < B \le 1$ the maximum value ![]() $1+B$ of the surfactant concentration is at the front of the bubble where
$1+B$ of the surfactant concentration is at the front of the bubble where ![]() $z=1$, the minimum value
$z=1$, the minimum value ![]() $1-B$ is at the rear of the bubble. In this case, according to (2.1), the surface tension at the front of the bubble is less than that at its rear and the bubble is expected to move to the right with some speed
$1-B$ is at the rear of the bubble. In this case, according to (2.1), the surface tension at the front of the bubble is less than that at its rear and the bubble is expected to move to the right with some speed ![]() $U_B(t)$ to be determined next. Being an even function of
$U_B(t)$ to be determined next. Being an even function of ![]() $s$, this initial surfactant concentration (5.9) is symmetric about the axis through the bubble centre, as required.
$s$, this initial surfactant concentration (5.9) is symmetric about the axis through the bubble centre, as required.
With the choice (5.7) it follows from the general solution (5.6) that
or, on rearrangement of the second equation,
For any given ![]() $t$ and
$t$ and ![]() $z$, the equation
$z$, the equation
must be solved for the unknown variable ![]() ${\mathcal {Z}} \equiv Bt/Z$. Therefore,
${\mathcal {Z}} \equiv Bt/Z$. Therefore,
where ![]() $\textrm {W}$ is the (zero branch of the) Lambert W-function (Olver et al. Reference Olver, Daalhuis, Lozier, Schneider, Boisvert, Clark, Mille, Saunders, Cohl and McClain2020). The analytic functions
$\textrm {W}$ is the (zero branch of the) Lambert W-function (Olver et al. Reference Olver, Daalhuis, Lozier, Schneider, Boisvert, Clark, Mille, Saunders, Cohl and McClain2020). The analytic functions ![]() $f(z,t)$ and
$f(z,t)$ and ![]() $g(z,t)$ associated with the quasi-steady Stokes flow generated around the bubble by the spreading surfactant can then be given explicitly in terms of this special function. Indeed,
$g(z,t)$ associated with the quasi-steady Stokes flow generated around the bubble by the spreading surfactant can then be given explicitly in terms of this special function. Indeed,
On substitution into (3.4) the streamfunction for the flow is
Furthermore, on setting ![]() $z= \textrm {e}^{-\textrm {i} s}$ the surfactant concentration and slip velocity are given as explicit functions of
$z= \textrm {e}^{-\textrm {i} s}$ the surfactant concentration and slip velocity are given as explicit functions of ![]() $s$ and
$s$ and ![]() $t$ by
$t$ by
Figure 3 shows the evolution of the surfactant concentration ![]() $\varGamma (s,t)$ and slip velocity
$\varGamma (s,t)$ and slip velocity ![]() $U(s,t)$ for
$U(s,t)$ for ![]() $Pe_s=\infty$ over the bubble boundary for
$Pe_s=\infty$ over the bubble boundary for ![]() $B=0.9$ in the initial condition (5.7) as computed from (5.16). The graphs show that as the surfactant spreads over the surface the Marangoni-stress-induced surface slip dies away until, at large times, it vanishes and the bubble motion is arrested.
$B=0.9$ in the initial condition (5.7) as computed from (5.16). The graphs show that as the surfactant spreads over the surface the Marangoni-stress-induced surface slip dies away until, at large times, it vanishes and the bubble motion is arrested.

Figure 3. Evolution of (a) the surfactant concentration ![]() $\varGamma (s,t)$ and (b) slip velocity
$\varGamma (s,t)$ and (b) slip velocity ![]() $U(s,t)$ for
$U(s,t)$ for ![]() $Pe_s=\infty$ over the bubble boundary for
$Pe_s=\infty$ over the bubble boundary for ![]() $B=0.9$ in the initial condition (5.7) as computed from (5.16). As the surfactant spreads over the surface the Marangoni-stress-induced surface slip dies away.
$B=0.9$ in the initial condition (5.7) as computed from (5.16). As the surfactant spreads over the surface the Marangoni-stress-induced surface slip dies away.
The bubble velocity ![]() $U_B(t)$ can be extracted as follows. Suppose that
$U_B(t)$ can be extracted as follows. Suppose that
Hence, using the non-dimensional versions of (3.5), (3.13) and (3.20):
which, by (2.7), leads to the identification
But since
then for large ![]() $z$,
$z$,
and hence
from which it follows, on comparing with (5.17), that ![]() $h_1(t) = B \,\textrm {e}^{-t}$. From (5.19), the bubble velocity is therefore
$h_1(t) = B \,\textrm {e}^{-t}$. From (5.19), the bubble velocity is therefore
The total bubble displacement ![]() $\Delta x$ due to the spreading of surfactant is
$\Delta x$ due to the spreading of surfactant is
Consequently, after the surface activity illustrated in the graphs of figure 3 and any further activity as ![]() $t \to \infty$, the bubble will have displaced to the right by a distance
$t \to \infty$, the bubble will have displaced to the right by a distance ![]() $B/2 = 0.45$.
$B/2 = 0.45$.
5.2. Formation of a weak singularity at finite time
The case ![]() $B=1$ is of special interest because, for this initial condition, the rear of the bubble is initially clean, i.e.
$B=1$ is of special interest because, for this initial condition, the rear of the bubble is initially clean, i.e. ![]() $\varGamma _0(\pm {\rm \pi})=0$, as is evident from (5.9). This turns out to have interesting consequences. Crowdy (Reference Crowdy2021b) has studied a similar circumstance of an isolated clean point existing in the initial surfactant distribution on the infinite free surface bounding a half-plane fluid layer and identified the formation of a weak singularity at finite time,
$\varGamma _0(\pm {\rm \pi})=0$, as is evident from (5.9). This turns out to have interesting consequences. Crowdy (Reference Crowdy2021b) has studied a similar circumstance of an isolated clean point existing in the initial surfactant distribution on the infinite free surface bounding a half-plane fluid layer and identified the formation of a weak singularity at finite time, ![]() $t_*$ say. During the ‘waiting time’
$t_*$ say. During the ‘waiting time’ ![]() $0 \le t < t_*$, before the singularity formation, the isolated clean point remains clean. At
$0 \le t < t_*$, before the singularity formation, the isolated clean point remains clean. At ![]() $t=t_*$ there is an instantaneous blow-up of the first derivatives
$t=t_*$ there is an instantaneous blow-up of the first derivatives ![]() $\partial \varGamma (s,t)/\partial s$ and
$\partial \varGamma (s,t)/\partial s$ and ![]() $\partial U(s,t)/\partial s$ at the clean point, but these do not lead to termination of the solution. Rather, the singularity is glancing and both
$\partial U(s,t)/\partial s$ at the clean point, but these do not lead to termination of the solution. Rather, the singularity is glancing and both ![]() $\partial \varGamma (s,t)/\partial s$ and
$\partial \varGamma (s,t)/\partial s$ and ![]() $\partial U(s,t)/\partial s$ return to finite values for
$\partial U(s,t)/\partial s$ return to finite values for ![]() $t > t_*$ with the clean point now being contaminated with surfactant. Since the discovery of this weak singularity in Crowdy (Reference Crowdy2021b), other authors have investigated similar phenomena in other circumstances but still in the semi-infinite fluid-layer geometry (Bickel & Detcheverry Reference Bickel and Detcheverry2022; Temprano-Coleto & Stone Reference Temprano-Coleto and Stone2024).
$t > t_*$ with the clean point now being contaminated with surfactant. Since the discovery of this weak singularity in Crowdy (Reference Crowdy2021b), other authors have investigated similar phenomena in other circumstances but still in the semi-infinite fluid-layer geometry (Bickel & Detcheverry Reference Bickel and Detcheverry2022; Temprano-Coleto & Stone Reference Temprano-Coleto and Stone2024).
The formation of an analogous weak singularity also occurs in the bubble geometry for the initial condition (5.7) when ![]() $B=1$ as is now shown. By the symmetry of this initial condition about the
$B=1$ as is now shown. By the symmetry of this initial condition about the ![]() $x$ axis the slip velocity at the rear of the bubble is necessarily zero at all times, i.e.
$x$ axis the slip velocity at the rear of the bubble is necessarily zero at all times, i.e. ![]() $U(\pm {\rm \pi},t)=0$, but let the surfactant concentration there be denoted by
$U(\pm {\rm \pi},t)=0$, but let the surfactant concentration there be denoted by ![]() $\varGamma _r(t)$, i.e.
$\varGamma _r(t)$, i.e.
It follows from (4.9) that
Crowdy (Reference Crowdy2021b) showed the existence of a finite-time weak singularity associated with an isolated clean point on the boundary of a half-plane fluid region by considering the dynamics of square-root branch-point singularities of (the relevant) ![]() $h(z,t)$ in the unphysical region of the complex plane. He showed that such a square-root branch-point reached the physical boundary in finite time (indeed, at the singularity formation time) but did not cause termination of the solution by entering the fluid region (where it is not allowed) but immediately turned around and re-entered the unphysical region of the complex plane thereby allowing a smooth continuation in time of the solution. For the bubble geometry, it is more convenient to demonstrate the weak singularity formation by returning to the implicit form of the solution given by (5.10) with
$h(z,t)$ in the unphysical region of the complex plane. He showed that such a square-root branch-point reached the physical boundary in finite time (indeed, at the singularity formation time) but did not cause termination of the solution by entering the fluid region (where it is not allowed) but immediately turned around and re-entered the unphysical region of the complex plane thereby allowing a smooth continuation in time of the solution. For the bubble geometry, it is more convenient to demonstrate the weak singularity formation by returning to the implicit form of the solution given by (5.10) with ![]() $B=1$. It follows that
$B=1$. It follows that
Hence,
which constitutes a nonlinear equation determining ![]() $\varGamma _r(t)$. A trivial solution is
$\varGamma _r(t)$. A trivial solution is ![]() $\varGamma _r(t)=0$ which corresponds to the rear of the bubble being clean. However, to explore the possibility of other solutions to this nonlinear equation for
$\varGamma _r(t)=0$ which corresponds to the rear of the bubble being clean. However, to explore the possibility of other solutions to this nonlinear equation for ![]() $\varGamma _r(t)$ it is useful to plot, as functions of
$\varGamma _r(t)$ it is useful to plot, as functions of ![]() $\varGamma _r \ge 0$, graphs of the two functions
$\varGamma _r \ge 0$, graphs of the two functions
and viewing ![]() $t$ as a parameter. This is done in figure 4 where the graph
$t$ as a parameter. This is done in figure 4 where the graph ![]() $y=\varGamma _r$, shown in black, is independent of
$y=\varGamma _r$, shown in black, is independent of ![]() $t$ and four instances of the graph
$t$ and four instances of the graph ![]() $y = 1 - \textrm {e}^{-t \varGamma _r}$, for
$y = 1 - \textrm {e}^{-t \varGamma _r}$, for ![]() $t=0.5$, 1, 1.5, 2 are shown in blue. According to (5.28) solutions for
$t=0.5$, 1, 1.5, 2 are shown in blue. According to (5.28) solutions for ![]() $\varGamma _r(t)$ occur where any blue graph intersects the black graph. The gradient
$\varGamma _r(t)$ occur where any blue graph intersects the black graph. The gradient ![]() ${\textrm {d}\kern 0.05em y}/\textrm {d}\varGamma _r$ of any graph of
${\textrm {d}\kern 0.05em y}/\textrm {d}\varGamma _r$ of any graph of ![]() $y = 1 - \textrm {e}^{-t \varGamma _r}$ is monotonic decreasing with its maximum value occurring at
$y = 1 - \textrm {e}^{-t \varGamma _r}$ is monotonic decreasing with its maximum value occurring at ![]() $\varGamma _r=0$. It is easy to see that
$\varGamma _r=0$. It is easy to see that ![]() $t=t_* = 1$ represents the critical case where the gradient of
$t=t_* = 1$ represents the critical case where the gradient of ![]() $y = 1 - \textrm {e}^{-t \varGamma _r}$ at
$y = 1 - \textrm {e}^{-t \varGamma _r}$ at ![]() $\varGamma _r=0$ is unity, the same as the gradient of the black curve
$\varGamma _r=0$ is unity, the same as the gradient of the black curve ![]() $y=\varGamma _r$ there. For
$y=\varGamma _r$ there. For ![]() $t > t_*=1$ the blue curves have a larger gradient than the black curve at
$t > t_*=1$ the blue curves have a larger gradient than the black curve at ![]() $\varGamma _r=0$ and it is clear geometrically from figure 4 that all blue graphs then curve down and have a single intersection point with the black curve at some value of
$\varGamma _r=0$ and it is clear geometrically from figure 4 that all blue graphs then curve down and have a single intersection point with the black curve at some value of ![]() $\varGamma _r > 0$: the value of
$\varGamma _r > 0$: the value of ![]() $\varGamma _r=\varGamma _r(t)$ at this intersection point for
$\varGamma _r=\varGamma _r(t)$ at this intersection point for ![]() $t > t_*$ is the surfactant concentration at the rear of the bubble after the weak singularity has occurred at
$t > t_*$ is the surfactant concentration at the rear of the bubble after the weak singularity has occurred at ![]() $t=t_*=1$. It is easy to show using local expansions that, just after the singularity formation time, a good leading-order approximation of
$t=t_*=1$. It is easy to show using local expansions that, just after the singularity formation time, a good leading-order approximation of ![]() $\varGamma _r(t)$ is furnished by
$\varGamma _r(t)$ is furnished by
Figure 5 features graphs of ![]() $\varGamma (s,t)$ and
$\varGamma (s,t)$ and ![]() $U(s,t)$ as functions of
$U(s,t)$ as functions of ![]() $s$, as computed from (5.16), both before and after
$s$, as computed from (5.16), both before and after ![]() $t=t_*=1$. These clearly show the instantaneous blow-up, and subsequent resolution, of the first derivatives
$t=t_*=1$. These clearly show the instantaneous blow-up, and subsequent resolution, of the first derivatives ![]() $\partial \varGamma (\pm {\rm \pi},1)/\partial s$ and
$\partial \varGamma (\pm {\rm \pi},1)/\partial s$ and ![]() $\partial U(\pm {\rm \pi},1)/\partial s$ at the rear of the bubble at
$\partial U(\pm {\rm \pi},1)/\partial s$ at the rear of the bubble at ![]() $t=t_*=1$.
$t=t_*=1$.
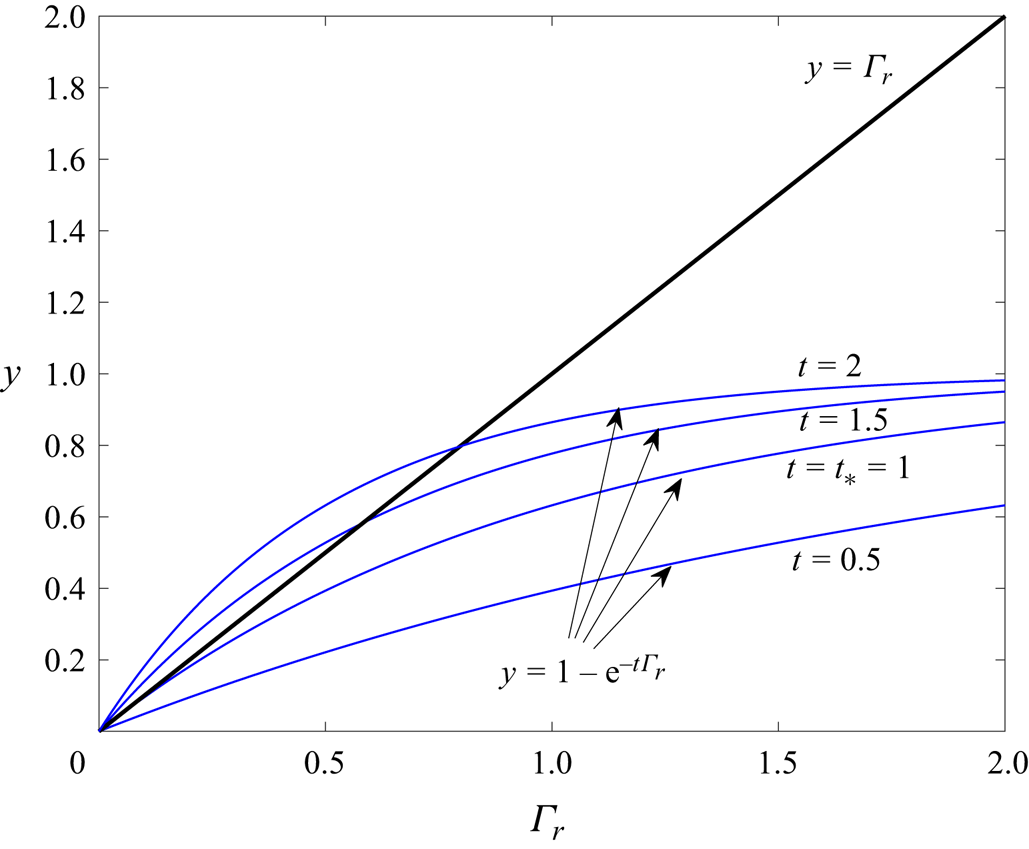
Figure 4. The two graphs (5.29) for different values of the parameter ![]() $t$. Admissible solutions for
$t$. Admissible solutions for ![]() $\varGamma _r(t)$ correspond to intersections of any blue graph of
$\varGamma _r(t)$ correspond to intersections of any blue graph of ![]() $y = 1 - \textrm {e}^{-t \varGamma _r}$ with the black graph
$y = 1 - \textrm {e}^{-t \varGamma _r}$ with the black graph ![]() $y=\varGamma _r$. From the geometry of these graphs the clean-point solution
$y=\varGamma _r$. From the geometry of these graphs the clean-point solution ![]() $\varGamma _r=0$ is the only admissible solution until
$\varGamma _r=0$ is the only admissible solution until ![]() $t > t_*=1$ when contamination of the rear of the bubble occurs.
$t > t_*=1$ when contamination of the rear of the bubble occurs.
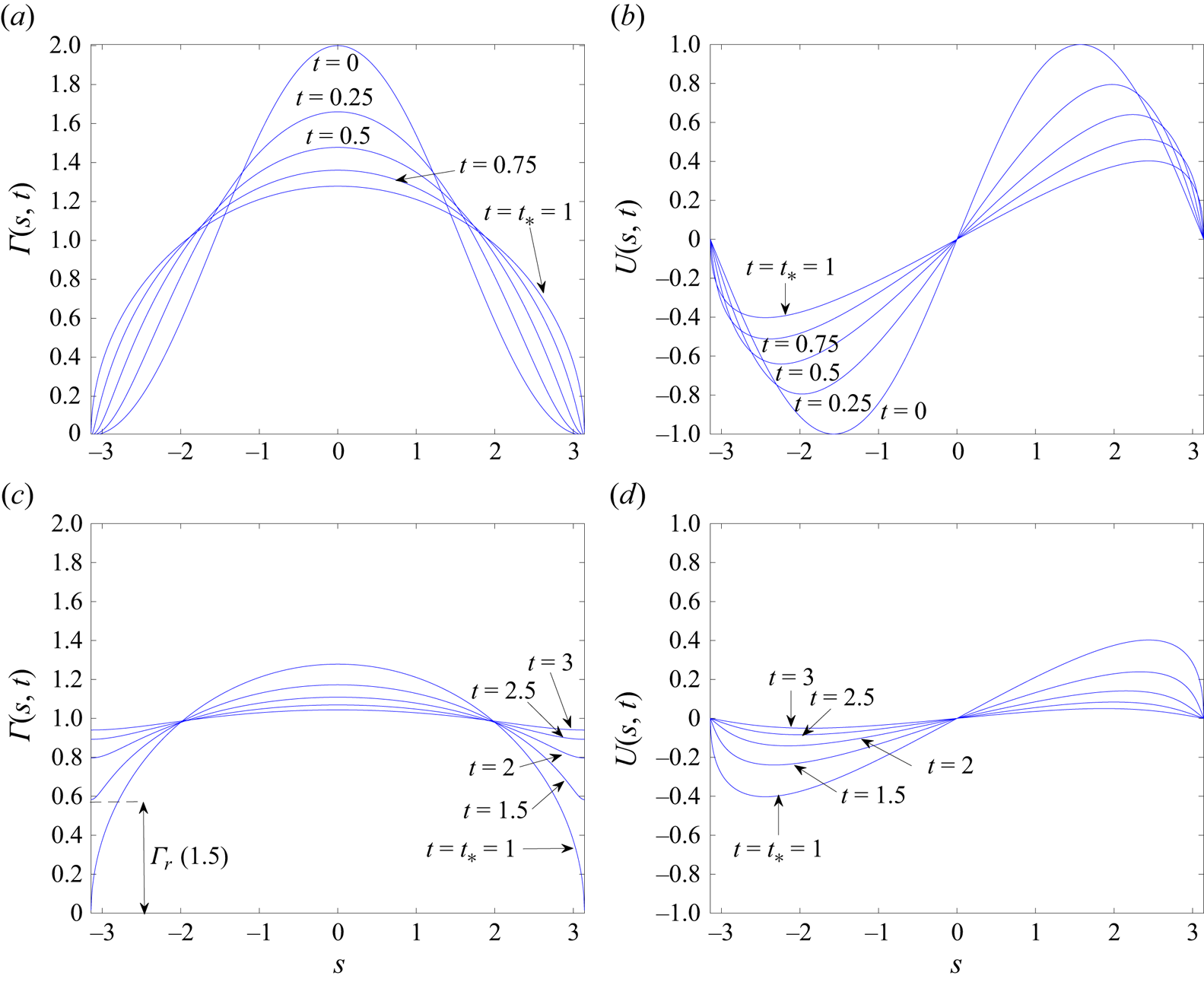
Figure 5. Formation of a weak singularity due to an isolated clean point at the rear of the bubble (at ![]() $s = \pm {\rm \pi}$) when
$s = \pm {\rm \pi}$) when ![]() $B=1$ in the initial condition (5.7). Plots of (a)
$B=1$ in the initial condition (5.7). Plots of (a) ![]() $\varGamma (s,t)$ and (b)
$\varGamma (s,t)$ and (b) ![]() $U(s,t)$ as a function of
$U(s,t)$ as a function of ![]() $s$ at
$s$ at ![]() $Pe_s=\infty$ for
$Pe_s=\infty$ for ![]() $t=0$, 0.25, 0.5, 0.75 and
$t=0$, 0.25, 0.5, 0.75 and ![]() $t=t_*=1$ where the weak singularity occurs. The rear of the bubble remains clean, i.e.
$t=t_*=1$ where the weak singularity occurs. The rear of the bubble remains clean, i.e. ![]() $\varGamma _r =0$, throughout the interval
$\varGamma _r =0$, throughout the interval ![]() $0 \le t \le t_*$. (c,d) The continuation past the singularity for
$0 \le t \le t_*$. (c,d) The continuation past the singularity for ![]() $t=t_*=1$, 1.5, 2, 2.5 and
$t=t_*=1$, 1.5, 2, 2.5 and ![]() $t=3$ where the rear of the bubble has become contaminated, i.e.
$t=3$ where the rear of the bubble has become contaminated, i.e. ![]() $\varGamma _r > 0$ for
$\varGamma _r > 0$ for ![]() $t > t_*=1$.
$t > t_*=1$.
This weak singularity formation in the surface variables does not affect any of the earlier deductions about the bubble speed ![]() $U_B(t)$ or net displacement
$U_B(t)$ or net displacement ![]() $\Delta x$. Therefore, after the surface activity illustrated in figure 5 and any further activity as
$\Delta x$. Therefore, after the surface activity illustrated in figure 5 and any further activity as ![]() $t \to \infty$, this bubble will have displaced to the right by a distance
$t \to \infty$, this bubble will have displaced to the right by a distance ![]() $\Delta x = B/2 = 0.5$ in accordance with (5.24).
$\Delta x = B/2 = 0.5$ in accordance with (5.24).
6. Bubble migration for  $0 < Pe_s < \infty$: a Cole–Hopf-type linearization
$0 < Pe_s < \infty$: a Cole–Hopf-type linearization
While the method of characteristics provides an implicit parametric representation of the general solution when ![]() $Pe_s$ is infinite, for
$Pe_s$ is infinite, for ![]() $0 < Pe_s < \infty$ the nonlinear problem turns out to be linearizable by a complex variant of the classical Cole–Hopf transformation (Whitham Reference Whitham1999). To see this, it is useful to view
$0 < Pe_s < \infty$ the nonlinear problem turns out to be linearizable by a complex variant of the classical Cole–Hopf transformation (Whitham Reference Whitham1999). To see this, it is useful to view ![]() $h(z,t)$ as a function of a new independent variable
$h(z,t)$ as a function of a new independent variable ![]() ${\mathcal {Z}}$ as follows:
${\mathcal {Z}}$ as follows:
Since ![]() $z {\partial /\partial z} = \partial /\partial {\mathcal {Z}}$ then (4.16) becomes
$z {\partial /\partial z} = \partial /\partial {\mathcal {Z}}$ then (4.16) becomes
which differs from a standard complex Burgers equation for ![]() ${\mathcal {H}}({\mathcal {Z}},t)$ only in the sign of the first term. Assuming the principal branch of the complex logarithm the domain of analyticity of
${\mathcal {H}}({\mathcal {Z}},t)$ only in the sign of the first term. Assuming the principal branch of the complex logarithm the domain of analyticity of ![]() ${\mathcal {H}}({\mathcal {Z}},t)$ is now the right semi-strip
${\mathcal {H}}({\mathcal {Z}},t)$ is now the right semi-strip ![]() $\textrm {Re}[{\mathcal {Z}}] \ge 0, -{\rm \pi} < \textrm {Im}[{\mathcal {Z}}] \le {\rm \pi}$ in the complex
$\textrm {Re}[{\mathcal {Z}}] \ge 0, -{\rm \pi} < \textrm {Im}[{\mathcal {Z}}] \le {\rm \pi}$ in the complex ![]() ${\mathcal {Z}}$ plane and admissible solutions must be
${\mathcal {Z}}$ plane and admissible solutions must be ![]() $2 {\rm \pi}\textrm {i}$-periodic as functions of
$2 {\rm \pi}\textrm {i}$-periodic as functions of ![]() ${\mathcal {Z}}$ in order that
${\mathcal {Z}}$ in order that ![]() $h(z,t)$ is a single-valued function in the fluid. A subsequent change of dependent variable embodied in
$h(z,t)$ is a single-valued function in the fluid. A subsequent change of dependent variable embodied in
where the second term on the right-hand side is assumed to decay as ![]() $z \to \infty$, turns (6.2) into
$z \to \infty$, turns (6.2) into
after an integration with respect to ![]() ${\mathcal {Z}}$ and where an additive function of time has been set equal to zero. The latter choice is made without loss of generality in the sense that any other choice simply rescales
${\mathcal {Z}}$ and where an additive function of time has been set equal to zero. The latter choice is made without loss of generality in the sense that any other choice simply rescales ![]() $\varPhi ({\mathcal {Z}},t)$ by a function of time which has no effect on the logarithmic
$\varPhi ({\mathcal {Z}},t)$ by a function of time which has no effect on the logarithmic ![]() ${\mathcal {Z}}$-derivative determining
${\mathcal {Z}}$-derivative determining ![]() ${\mathcal {H}}({\mathcal {Z}},t)$ in (6.3) and, as such, does not affect the physical flow.
${\mathcal {H}}({\mathcal {Z}},t)$ in (6.3) and, as such, does not affect the physical flow.
Equation (6.3) is a complex variant of the classical Cole–Hopf transformation (Whitham Reference Whitham1999) differing from it not only because it involves complex-valued functions and variables, but also in the appearance of the first unity term in (6.3). This results in the modified form (6.4) of the classical heat equation; the latter equation is the linear partial differential equation arising after carrying out a standard Cole–Hopf transformation on the real Burgers equation. The important observation is that, even if it is not the usual heat equation, (6.4) is still nevertheless a linear partial differential equation, albeit a complex-valued one.
In view of its linear character it is natural to seek separable solutions of (6.4) having the form
this being a general representation of a ![]() $2 {\rm \pi}\textrm {i}$-periodic function that is analytic in the right semi-strip and decaying as
$2 {\rm \pi}\textrm {i}$-periodic function that is analytic in the right semi-strip and decaying as ![]() $\textrm {Re}[{\mathcal {Z}}] \to \infty$. These properties are necessary to ensure that
$\textrm {Re}[{\mathcal {Z}}] \to \infty$. These properties are necessary to ensure that ![]() ${\mathcal {H}}({\mathcal {Z}},t)$ as given by (6.3) gives rise, according to (6.1), to a function
${\mathcal {H}}({\mathcal {Z}},t)$ as given by (6.3) gives rise, according to (6.1), to a function ![]() $h(z,t)$ with the required properties. Substitution of (6.5) into (6.4) leads to the linear system
$h(z,t)$ with the required properties. Substitution of (6.5) into (6.4) leads to the linear system
The solutions of these ordinary differential equations are
where the data ![]() $\{ A_{n0} = A_n(0) | n \ge 0 \}$ are determined by initial conditions. The solution for
$\{ A_{n0} = A_n(0) | n \ge 0 \}$ are determined by initial conditions. The solution for ![]() $\varPhi ({\mathcal {Z}},t)$ follows as
$\varPhi ({\mathcal {Z}},t)$ follows as
giving
 \begin{equation} {\mathcal{H}}({\mathcal{Z}},t) = 1 + \frac{2 }{Pe_s} \frac{\displaystyle\sum_{n \ge 1} n A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}} }{\displaystyle\sum_{n \ge 0} A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}}} \end{equation}
\begin{equation} {\mathcal{H}}({\mathcal{Z}},t) = 1 + \frac{2 }{Pe_s} \frac{\displaystyle\sum_{n \ge 1} n A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}} }{\displaystyle\sum_{n \ge 0} A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}}} \end{equation}or, on back substitution into (6.3) and from (6.1),
 \begin{equation} h(z,t) = 1 + \frac{2 }{Pe_s} \frac{\displaystyle\sum_{n \ge 1} n A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t}/z^n }{\displaystyle\sum_{n \ge 0} A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t}/z^n }. \end{equation}
\begin{equation} h(z,t) = 1 + \frac{2 }{Pe_s} \frac{\displaystyle\sum_{n \ge 1} n A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t}/z^n }{\displaystyle\sum_{n \ge 0} A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t}/z^n }. \end{equation}
This is an explicit solution for arbitrary initial data and for any finite non-zero value of ![]() $Pe_s$.
$Pe_s$.
Consider now the initial conditions (5.7) for which the ![]() $Pe_s=\infty$ solution has been found in § 5.1 in terms of Lambert-W functions. It is of interest to examine how surface diffusion affects this solution. For this it is necessary to pick
$Pe_s=\infty$ solution has been found in § 5.1 in terms of Lambert-W functions. It is of interest to examine how surface diffusion affects this solution. For this it is necessary to pick
from which it follows that
Substitution of these coefficients into (6.10) gives the solution for ![]() $h(z,t)$. The speed of the bubble
$h(z,t)$. The speed of the bubble ![]() $U_B(t)$ follows from the large-
$U_B(t)$ follows from the large-![]() $z$ asymptotics of (6.10). As
$z$ asymptotics of (6.10). As ![]() $z \to \infty$,
$z \to \infty$,
so that, from (5.19),
and
As ![]() $Pe_s \to \infty$, the results (6.14) and (6.15) tend, respectively, to (5.23) and (5.24), as expected. On comparing (5.23) and (6.14) surface diffusion is seen to slow down the bubble and, on comparing (5.24) and (6.15), to reduce its total displacement.
$Pe_s \to \infty$, the results (6.14) and (6.15) tend, respectively, to (5.23) and (5.24), as expected. On comparing (5.23) and (6.14) surface diffusion is seen to slow down the bubble and, on comparing (5.24) and (6.15), to reduce its total displacement.
Figure 6 compares the evolution of the surfactant concentration ![]() $\varGamma (s,t)$ at finite
$\varGamma (s,t)$ at finite ![]() $Pe_s=10$ and
$Pe_s=10$ and ![]() $1$ with the analogous evolution in the case of infinite
$1$ with the analogous evolution in the case of infinite ![]() $Pe_s$ for the initial condition (5.7) with
$Pe_s$ for the initial condition (5.7) with ![]() $B=0.5$. In the absence of any additional forcing, surface diffusion aids in more quickly mollifying any surfactant concentration gradients and effectively enhances the rate of surfactant spreading to the uniform coverage state. As a result, the overall displacement of the bubble lessens with enhanced surface diffusion, i.e. as
$B=0.5$. In the absence of any additional forcing, surface diffusion aids in more quickly mollifying any surfactant concentration gradients and effectively enhances the rate of surfactant spreading to the uniform coverage state. As a result, the overall displacement of the bubble lessens with enhanced surface diffusion, i.e. as ![]() $Pe_s$ decreases, a feature that is apparent from formula (6.15). The total bubble displacements after the surface activity shown in figure 6 for
$Pe_s$ decreases, a feature that is apparent from formula (6.15). The total bubble displacements after the surface activity shown in figure 6 for ![]() $Pe_s=\infty$,
$Pe_s=\infty$, ![]() $10$ and
$10$ and ![]() $1$ are
$1$ are ![]() $0.2500$,
$0.2500$, ![]() $0.2273$ and
$0.2273$ and ![]() $0.1250$, respectively.
$0.1250$, respectively.

Figure 6. The effect of surface diffusion. The graphs compare the evolution of the surfactant concentration ![]() $\varGamma (s,t)$ for
$\varGamma (s,t)$ for ![]() $Pe_s=10$ and
$Pe_s=10$ and ![]() $\infty$ (a) and for
$\infty$ (a) and for ![]() $Pe_s=1$ and
$Pe_s=1$ and ![]() $\infty$ (b) for the initial condition (5.7) with
$\infty$ (b) for the initial condition (5.7) with ![]() $B=0.5$. The concentrations for
$B=0.5$. The concentrations for ![]() $Pe_s=\infty$ are shown as solid blue lines, the finite-
$Pe_s=\infty$ are shown as solid blue lines, the finite-![]() $Pe_s$ results as dashed red lines.
$Pe_s$ results as dashed red lines.
It is worth pointing out that, by a further simple change of variables, the governing equation (6.4) can be transformed to the backwards complex heat equation. At first sight, this may cause concern given the ill-posedness of many problems involving the real-valued backwards heat equation. However, in this case, as has been seen by explicit construction of the solution, this complex version is solved within a class of complex-valued analytic functions for which the evolution problem is well posed.
7. General initial surfactant distributions
The special initial condition (5.9) corresponds to a distribution with a well-defined excess of surfactant at the front of the bubble that falls off, symmetrically with respect to the ![]() $x$ axis, towards its rear. Can anything be said if the initial surfactant distribution has a more variegated profile, perhaps with a series of humps and troughs, though still symmetric with respect to the real axis?
$x$ axis, towards its rear. Can anything be said if the initial surfactant distribution has a more variegated profile, perhaps with a series of humps and troughs, though still symmetric with respect to the real axis?
For the case of infinite surface Péclet number the implicit general solution (5.6) encodes the dynamics, and it is easy to use this as a basis for a numerical computation of the solution, but it is not generally possible to make this solution explicit as done for the special initial condition considered in § 5.1. Nevertheless, quantitative statements about the velocity ![]() $U_B(t)$ and total displacement
$U_B(t)$ and total displacement ![]() $\Delta x$ for more general initial surfactant distributions can still be made. For a more general, sufficiently smooth, initial surfactant distribution
$\Delta x$ for more general initial surfactant distributions can still be made. For a more general, sufficiently smooth, initial surfactant distribution ![]() $\varGamma (s,0)= \varGamma _0(s)$ that is symmetric about the
$\varGamma (s,0)= \varGamma _0(s)$ that is symmetric about the ![]() $x$ axis the associated
$x$ axis the associated ![]() $H(Z)$ will have, on
$H(Z)$ will have, on ![]() $|Z|=1$, a convergent Laurent series of the form
$|Z|=1$, a convergent Laurent series of the form
By the assumed symmetry about the real axis, all the series coefficients ![]() $\{ B_n | n=1,2, \ldots \}$ will be real so that, on taking the real part of (7.1) to find the initial surfactant concentration it will have a Fourier cosine expansion in
$\{ B_n | n=1,2, \ldots \}$ will be real so that, on taking the real part of (7.1) to find the initial surfactant concentration it will have a Fourier cosine expansion in ![]() $s$. In particular,
$s$. In particular,
It is straightforward to show, by extending the far-field asymptotics of § 5, that the speed of the bubble ![]() $U_B(t)$ and total displacement
$U_B(t)$ and total displacement ![]() $\Delta x$ are
$\Delta x$ are
which constitutes a quite general result. In summary, and returning now to dimensional variables, at infinite surface Péclet number, for any initial surfactant concentration ![]() $\varGamma _0(s)$, symmetric about the
$\varGamma _0(s)$, symmetric about the ![]() $x$ axis, the bubble velocity and its total displacement in the
$x$ axis, the bubble velocity and its total displacement in the ![]() $x$ direction are given by
$x$ direction are given by
 \begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle U_B(t) = \dfrac{\beta }{4 {\rm \pi}\mu {\mathcal{R}} } \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \} \exp \left ( - \dfrac{\beta \langle \varGamma_0 \rangle t }{2 \mu {\mathcal{R}}} \right ), \\ \displaystyle \Delta x = \dfrac{1 }{2 {\rm \pi}\langle \varGamma_0 \rangle} \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \}, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle U_B(t) = \dfrac{\beta }{4 {\rm \pi}\mu {\mathcal{R}} } \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \} \exp \left ( - \dfrac{\beta \langle \varGamma_0 \rangle t }{2 \mu {\mathcal{R}}} \right ), \\ \displaystyle \Delta x = \dfrac{1 }{2 {\rm \pi}\langle \varGamma_0 \rangle} \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \}, \end{array}\right\} \end{equation}
where ![]() $\langle \varGamma _0 \rangle$ is the average surfactant concentration.
$\langle \varGamma _0 \rangle$ is the average surfactant concentration.
Similarly, a straightforward generalization to arbitrary initial conditions of the calculation given in § 6 for ![]() $0 < Pe_s < \infty$ leads to
$0 < Pe_s < \infty$ leads to
 \begin{equation}
\left.\begin{array}{@{}c@{}} \displaystyle U_B(t) =
\dfrac{\beta }{4 {\rm \pi}\mu {\mathcal{R}} } \left\{
\int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}}
\varGamma_0(s) \cos \left (\dfrac{s}{{\mathcal{R}}}
\right ) {\rm d} s \right \} \exp \left ( - \dfrac{\beta
\langle \varGamma_0 \rangle (1+1/Pe_s) t }{2 \mu
{\mathcal{R}}} \right ), \\ \displaystyle \Delta x =
\dfrac{1 }{2 {\rm \pi}\langle \varGamma_0 \rangle(1+1/Pe_s)}
\left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}}
\varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right
) {\rm d} s \right \}. \end{array}\right\}
\end{equation}
\begin{equation}
\left.\begin{array}{@{}c@{}} \displaystyle U_B(t) =
\dfrac{\beta }{4 {\rm \pi}\mu {\mathcal{R}} } \left\{
\int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}}
\varGamma_0(s) \cos \left (\dfrac{s}{{\mathcal{R}}}
\right ) {\rm d} s \right \} \exp \left ( - \dfrac{\beta
\langle \varGamma_0 \rangle (1+1/Pe_s) t }{2 \mu
{\mathcal{R}}} \right ), \\ \displaystyle \Delta x =
\dfrac{1 }{2 {\rm \pi}\langle \varGamma_0 \rangle(1+1/Pe_s)}
\left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}}
\varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right
) {\rm d} s \right \}. \end{array}\right\}
\end{equation}
Formulas (7.5) reduce to formulas (7.4) as ![]() $Pe_s \to \infty$, as expected.
$Pe_s \to \infty$, as expected.
It is interesting that the net displacement depends only on the first two coefficients in a Fourier cosine series of the initial surfactant concentration: the coefficient ![]() $B_1$ is the second term in a Fourier cosine series of the initial surfactant concentration, the first term being the average surfactant concentration over the surface. The net bubble displacement is proportional to the ratio of these first two Fourier cosine coefficients with the constant of proportionality being a simple function of the surface Péclet number. Similar observations on the importance of a small number of early coefficients in the relevant series expansions determining the overall behaviour have been made in other problems of low-Reynolds-number locomotion driven by different surface actuation mechanisms (Crowdy Reference Crowdy2013).
$B_1$ is the second term in a Fourier cosine series of the initial surfactant concentration, the first term being the average surfactant concentration over the surface. The net bubble displacement is proportional to the ratio of these first two Fourier cosine coefficients with the constant of proportionality being a simple function of the surface Péclet number. Similar observations on the importance of a small number of early coefficients in the relevant series expansions determining the overall behaviour have been made in other problems of low-Reynolds-number locomotion driven by different surface actuation mechanisms (Crowdy Reference Crowdy2013).
8. From inviscid bubbles to viscous droplets
The analysis of this paper generalizes easily to the two-fluid scenario where the inviscid bubble is replaced by a droplet of viscous fluid of different viscosity. The key steps are the same as for the two-fluid generalization carried out by Crowdy, Curran & Papageorgiou (Reference Crowdy, Curran and Papageorgiou2023) of the earlier single-fluid analysis of Crowdy (Reference Crowdy2021b,Reference Crowdyc) in the half-plane fluid geometry so they will only be sketched out here.
Suppose the outer fluid viscosity, which has been denoted throughout this paper by ![]() $\mu$, is now called
$\mu$, is now called ![]() $\mu _+$ with the generally different viscosity of the droplet fluid in
$\mu _+$ with the generally different viscosity of the droplet fluid in ![]() $|z| <1$ denoted by
$|z| <1$ denoted by ![]() $\mu _-$. It is natural to define corresponding Goursat functions
$\mu _-$. It is natural to define corresponding Goursat functions ![]() $\hat f_\pm (z,t)$ and
$\hat f_\pm (z,t)$ and ![]() $g_\pm (z,t)$ in the two viscous fluid regions, and two corresponding functions
$g_\pm (z,t)$ in the two viscous fluid regions, and two corresponding functions
As done earlier, the functional relationships
are imposed. The requirement that the tangential fluid velocities at the boundary of the droplet where the two fluids meet must be continuous turns out to furnish the following functional relationship:
where ![]() $\overline{q}(z,t)\equiv \overline {q(\bar {z},t)}$ denotes the usual Schwarz conjugate of an analytic function
$\overline{q}(z,t)\equiv \overline {q(\bar {z},t)}$ denotes the usual Schwarz conjugate of an analytic function ![]() $q(z,t)$. The relation (8.3) means that there is a reflectional symmetry between the inner and outer Stokes flow solutions in this circular geometry. A similar observation was made by Crowdy et al. (Reference Crowdy, Curran and Papageorgiou2023) for the two fluids in neighbouring half-planes meeting at the flat interface between them. At small capillary number, there is still a leading-order Laplace–Young balance of normal fluid stresses on the boundary while the tangential stress condition now involves boundary tractions from both fluids balancing the Marangoni stress due to the surfactant. Ultimately, the principal modification to the analysis here is to replace
$q(z,t)$. The relation (8.3) means that there is a reflectional symmetry between the inner and outer Stokes flow solutions in this circular geometry. A similar observation was made by Crowdy et al. (Reference Crowdy, Curran and Papageorgiou2023) for the two fluids in neighbouring half-planes meeting at the flat interface between them. At small capillary number, there is still a leading-order Laplace–Young balance of normal fluid stresses on the boundary while the tangential stress condition now involves boundary tractions from both fluids balancing the Marangoni stress due to the surfactant. Ultimately, the principal modification to the analysis here is to replace ![]() $\mu$ by
$\mu$ by ![]() $(\mu _++\mu _-)$ and replace the characteristic velocity scaling
$(\mu _++\mu _-)$ and replace the characteristic velocity scaling ![]() $U_0$ given in (4.1) by
$U_0$ given in (4.1) by
This clearly reduces to (4.1) when ![]() $\mu _-=0$.
$\mu _-=0$.
9. Discussion
A simple model of viscous Marangoni migration of a two-dimensional bubble by surfactant spreading has been proposed and shown to be exactly solvable mathematically at all non-zero values of the surface Péclet number, including when surface diffusion is completely absent, or ![]() $Pe_s=\infty$. The work can be viewed as complementing a body of theoretical work on viscous Marangoni propulsion in the diffusion-dominated regime when the surface Péclet number vanishes and the problem becomes intrinsically linear (Lauga & Davis Reference Lauga and Davis2011; Crowdy Reference Crowdy2020, Reference Crowdy2021a). Surprisingly, as has been shown here, if surface advection is included the now apparently nonlinear problem can, in fact, also be linearized. While the formulation is valid for any
$Pe_s=\infty$. The work can be viewed as complementing a body of theoretical work on viscous Marangoni propulsion in the diffusion-dominated regime when the surface Péclet number vanishes and the problem becomes intrinsically linear (Lauga & Davis Reference Lauga and Davis2011; Crowdy Reference Crowdy2020, Reference Crowdy2021a). Surprisingly, as has been shown here, if surface advection is included the now apparently nonlinear problem can, in fact, also be linearized. While the formulation is valid for any ![]() $Pe_s > 0$ note that since both the Reynolds number and capillary number depend on the size of
$Pe_s > 0$ note that since both the Reynolds number and capillary number depend on the size of ![]() $U_0$, care must be taken to ensure the theory herein is only applied in circumstances where this velocity is such that the assumptions of low Reynolds and capillary numbers can safely be made.
$U_0$, care must be taken to ensure the theory herein is only applied in circumstances where this velocity is such that the assumptions of low Reynolds and capillary numbers can safely be made.
The results here rely on a complex variable formulation of the Stokes flow problem characterized by a coupled analytical description of the surfactant and flow dynamics in terms of a single-valued analytic function ![]() $h(z,t)$ that is shown to satisfy a complex partial differential equation of Burgers type. At finite non-zero surface Péclet number, this reformulation is combined with further changes of variable generalizing the classical Cole–Hopf transformation revealing that this nonlinear problem is linearizable at any finite non-zero surface Péclet number. The governing linear complex partial differential equation is (6.4). This linearization is expected to have significant theoretical and numerical ramifications beyond those already set out here. Useful general formulas (7.4) and (7.5) show precisely how details of the initial surfactant distribution govern the bubble speed and its net displacement after long times. It is reasonable to conjecture that similar formulas might hold for a three-dimensional spherical bubble although that suggestion requires further investigation since none of the mathematical techniques used here carry over to that case.
$h(z,t)$ that is shown to satisfy a complex partial differential equation of Burgers type. At finite non-zero surface Péclet number, this reformulation is combined with further changes of variable generalizing the classical Cole–Hopf transformation revealing that this nonlinear problem is linearizable at any finite non-zero surface Péclet number. The governing linear complex partial differential equation is (6.4). This linearization is expected to have significant theoretical and numerical ramifications beyond those already set out here. Useful general formulas (7.4) and (7.5) show precisely how details of the initial surfactant distribution govern the bubble speed and its net displacement after long times. It is reasonable to conjecture that similar formulas might hold for a three-dimensional spherical bubble although that suggestion requires further investigation since none of the mathematical techniques used here carry over to that case.
In addition to characterizing the migration properties of the bubble due to surfactant spreading, the surface activity has also been fully resolved. Of particular note is the formation of a weak singularity: it is the analogue of a similar singularity first observed by Crowdy (Reference Crowdy2021b) in the half-plane fluid geometry and is associated with an isolated clean point on the free surface. Up to a well-defined finite (‘waiting’) time ![]() $t_*$ this clean point remains free of surfactant but, at
$t_*$ this clean point remains free of surfactant but, at ![]() $t=t_*$, the quantities
$t=t_*$, the quantities ![]() $\partial \varGamma /\partial s$ and
$\partial \varGamma /\partial s$ and ![]() $\partial U/\partial s$ become infinite simultaneously at this clean point and resolve back to finite values for
$\partial U/\partial s$ become infinite simultaneously at this clean point and resolve back to finite values for ![]() $t > t_*$ and the formerly clean point is now contaminated with surfactant. This interesting singularity is designated weak because, while certain derivative quantities exhibit instantaneous blow-up at
$t > t_*$ and the formerly clean point is now contaminated with surfactant. This interesting singularity is designated weak because, while certain derivative quantities exhibit instantaneous blow-up at ![]() $t_*$, the flow itself remains finite and continues to exist beyond
$t_*$, the flow itself remains finite and continues to exist beyond ![]() $t_*$. Bickel & Detcheverry (Reference Bickel and Detcheverry2022) and Temprano-Coleto & Stone (Reference Temprano-Coleto and Stone2024) have recently used the complex Burgers equation formulation of Crowdy (Reference Crowdy2021b,Reference Crowdyc) to study such singularity formation in more detail by studying other solution types such as similarity solutions. Since the real Burgers equation is the paradigmatic nonlinear equation exhibiting shock formation in the absence of any (viscous) regularization, and since it is also known that there are circumstances in which ‘surfactant shocks’ can occur in Marangoni flows (Jensen & Grotberg Reference Jensen and Grotberg1992), it is natural to ask if any phenomena akin to shock formation are observable within the viscous Marangoni regime shown here to be describable by a complex-valued Burgers-type partial differential equation. Crowdy (Reference Crowdy2021b) briefly discussed this issue from the perspective of the more general question of well-posedness of solutions of the complex Burgers equation and suggested, based on empirical observations, that the physical requirement that
$t_*$. Bickel & Detcheverry (Reference Bickel and Detcheverry2022) and Temprano-Coleto & Stone (Reference Temprano-Coleto and Stone2024) have recently used the complex Burgers equation formulation of Crowdy (Reference Crowdy2021b,Reference Crowdyc) to study such singularity formation in more detail by studying other solution types such as similarity solutions. Since the real Burgers equation is the paradigmatic nonlinear equation exhibiting shock formation in the absence of any (viscous) regularization, and since it is also known that there are circumstances in which ‘surfactant shocks’ can occur in Marangoni flows (Jensen & Grotberg Reference Jensen and Grotberg1992), it is natural to ask if any phenomena akin to shock formation are observable within the viscous Marangoni regime shown here to be describable by a complex-valued Burgers-type partial differential equation. Crowdy (Reference Crowdy2021b) briefly discussed this issue from the perspective of the more general question of well-posedness of solutions of the complex Burgers equation and suggested, based on empirical observations, that the physical requirement that ![]() $\varGamma \ge 0$ on the interface, which is specific to the Marangoni flow application, may preclude the formation of any finite-time singularities such as shocks. In very recent work, and by making associations with the more general literature on transport equations involving Hilbert transforms, Temprano-Coleto & Stone (Reference Temprano-Coleto and Stone2024) have offered evidence to support this suggestion. It should be noted that surfactant shock formation has been observed in quite different geometrical set-ups involving thin fluid layers (Jensen & Grotberg Reference Jensen and Grotberg1992) which is not a characteristic of the radial bubble geometry of the present paper, or in the previous work of Crowdy (Reference Crowdy2021b,Reference Crowdyc) where a mathematical description in terms of a complex Burgers equation was shown to be relevant to infinitely deep viscous fluid layers.
$\varGamma \ge 0$ on the interface, which is specific to the Marangoni flow application, may preclude the formation of any finite-time singularities such as shocks. In very recent work, and by making associations with the more general literature on transport equations involving Hilbert transforms, Temprano-Coleto & Stone (Reference Temprano-Coleto and Stone2024) have offered evidence to support this suggestion. It should be noted that surfactant shock formation has been observed in quite different geometrical set-ups involving thin fluid layers (Jensen & Grotberg Reference Jensen and Grotberg1992) which is not a characteristic of the radial bubble geometry of the present paper, or in the previous work of Crowdy (Reference Crowdy2021b,Reference Crowdyc) where a mathematical description in terms of a complex Burgers equation was shown to be relevant to infinitely deep viscous fluid layers.
The availability of analytical solutions is valuable when adding in other effects perturbatively by assuming they are small. A few obvious extensions to the work here are to include the effect of weak inertia (small but non-zero Reynolds number), weak deformability of the bubble and weak solubility of the surfactant to the bulk.
Finally, since the connection of Marangoni dynamics to the complex Burgers equation was unveiled in the half-plane fluid geometry by Crowdy (Reference Crowdy2021b,Reference Crowdyc), several further theoretical advances have been made in the semi-infinite geometry (Bickel & Detcheverry Reference Bickel and Detcheverry2022; Crowdy et al. Reference Crowdy, Curran and Papageorgiou2023; Temprano-Coleto & Stone Reference Temprano-Coleto and Stone2024). The present paper extends these new theoretical developments in a different direction, namely to the radial bubble geometry. It is likely that this new formulation will similarly pave the way for other advances in understanding Marangoni flows involving bubbles and droplets. Among additional physical effects that are amenable to a similar formulation are thermocapillarity (Young et al. Reference Young, Goldstein and Block1959), reaction effects (Crowdy Reference Crowdy2021b) and solubility of the surfactant (Crowdy et al. Reference Crowdy, Curran and Papageorgiou2023) and progress in these directions will be reported elsewhere.
Funding
This work was funded by EPSRC Grant EP/V062298/1.
Declaration of interests
The author reports no conflict of interest.