Article contents
Viscous irrotational analysis of the deformation and break-up time of a bubble or drop in uniaxial straining flow*
Published online by Cambridge University Press: 09 November 2011
Abstract
The nonlinear deformation and break-up of a bubble or drop immersed in a uniaxial extensional flow of an incompressible viscous fluid is analysed by means of viscous potential flow. In this approximation, the flow field is irrotational and viscosity enters through the balance of normal stresses at the interface. The governing equations are solved numerically to track the motion of the interface by coupling a boundary-element method with a time-integration routine. When break-up occurs, the break-up time computed here is compared with results obtained elsewhere from numerical simulations of the Navier–Stokes equations (Revuelta, Rodríguez-Rodríguez & Martínez-Bazán J. Fluid Mech., vol. 551, 2006, p. 175), which thus keeps vorticity in the analysis, for several combinations of the relevant dimensionless parameters of the problem. For the bubble, for Weber numbers 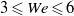 , predictions from viscous potential flow shows good agreement with the results from the Navier–Stokes equations for the bubble break-up time, whereas for larger
, predictions from viscous potential flow shows good agreement with the results from the Navier–Stokes equations for the bubble break-up time, whereas for larger 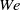 , the former underpredicts the results given by the latter. When viscosity is included, larger break-up times are predicted with respect to the inviscid case for the same
, the former underpredicts the results given by the latter. When viscosity is included, larger break-up times are predicted with respect to the inviscid case for the same 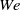 . For the drop, and considering moderate Reynolds numbers,
. For the drop, and considering moderate Reynolds numbers, 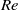 , increasing the viscous effects of the irrotational motion produces large, elongated drops that take longer to break up in comparison with results for inviscid fluids. For larger
, increasing the viscous effects of the irrotational motion produces large, elongated drops that take longer to break up in comparison with results for inviscid fluids. For larger 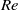 , it comes as a surprise that break-up times smaller than the inviscid limit are obtained. Unfortunately, results from numerical analyses of the incompressible, unsteady Navier–Stokes equations for the case of a drop have not been presented in the literature, to the best of the authors’ knowledge; hence, comparison with the viscous irrotational analysis is not possible.
, it comes as a surprise that break-up times smaller than the inviscid limit are obtained. Unfortunately, results from numerical analyses of the incompressible, unsteady Navier–Stokes equations for the case of a drop have not been presented in the literature, to the best of the authors’ knowledge; hence, comparison with the viscous irrotational analysis is not possible.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
Footnotes
This paper is dedicated to the memory of Daniel D. Joseph (1929–2011).
References
- 2
- Cited by


