Published online by Cambridge University Press: 11 December 2017
Fluid–structure interactions are ubiquitous in nature and technology. However, the systems are often so complex that numerical simulations or ad hoc assumptions must be used to gain insight into the details of the complex interactions between the fluid and solid mechanics. In this paper, we present experiments and theory on viscous flow in a simple bioinspired soft valve which illustrate essential features of interactions between hydrodynamic and elastic forces at low Reynolds numbers. The set-up comprises a sphere connected to a spring located inside a tapering cylindrical channel. The spring is aligned with the central axis of the channel and a pressure drop is applied across the sphere, thus forcing the liquid through the narrow gap between the sphere and the channel walls. The sphere’s equilibrium position is determined by a balance between spring and hydrodynamic forces. Since the gap thickness changes with the sphere’s position, the system has a pressure-dependent hydraulic resistance. This leads to a nonlinear relation between applied pressure and flow rate: flow initially increases with pressure, but decreases when the pressure exceeds a certain critical value as the gap closes. To rationalize these observations, we propose a mathematical model that reduced the complexity of the flow to a two-dimensional lubrication approximation. A closed-form expression for the pressure drop/flow rate is obtained which reveals that the flow rate 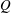 $Q$ depends on the pressure drop
$Q$ depends on the pressure drop 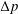 $\unicode[STIX]{x0394}p$, sphere radius
$\unicode[STIX]{x0394}p$, sphere radius  $a$, gap thickness
$a$, gap thickness 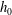 $h_{0}$, and viscosity
$h_{0}$, and viscosity 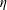 $\unicode[STIX]{x1D702}$ as
$\unicode[STIX]{x1D702}$ as  $Q\sim \unicode[STIX]{x1D702}^{-1}a^{1/2}h_{0}^{5/2}(1-\unicode[STIX]{x0394}p/\unicode[STIX]{x0394}p_{c})^{5/2}\unicode[STIX]{x0394}p$, where the critical pressure
$Q\sim \unicode[STIX]{x1D702}^{-1}a^{1/2}h_{0}^{5/2}(1-\unicode[STIX]{x0394}p/\unicode[STIX]{x0394}p_{c})^{5/2}\unicode[STIX]{x0394}p$, where the critical pressure 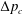 $\unicode[STIX]{x0394}p_{c}$ scales with the spring constant
$\unicode[STIX]{x0394}p_{c}$ scales with the spring constant 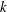 $k$ as
$k$ as 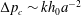 $\unicode[STIX]{x0394}p_{c}\sim kh_{0}a^{-2}$. These predictions compared favourably to the results of our experiments with no free parameters.
$\unicode[STIX]{x0394}p_{c}\sim kh_{0}a^{-2}$. These predictions compared favourably to the results of our experiments with no free parameters.
Experimental movie of a soft valve with water and $z_d$ = 3.6 mm. The observed oscillation frequency is $f_{ ext{obs}}$ ~ 2.7 Hz, which is significantly slower than the systems's spring-mass oscillation frequency $f_{ ext{spring}}=1/(2\pi)(k/m)^{1/2}=32$ Hz.