Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T14:02:01.397Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous effects on the fundamental solution to ship waves

Published online by Cambridge University Press:  01 October 2019

Hui Liang Open the ORCID record for Hui Liang [Opens in a new window]  and
Xiaobo Chen Open the ORCID record for Xiaobo Chen [Opens in a new window]
Hui Liang*
Affiliation:
Technology Centre for Offshore and Marine, Singapore (TCOMS), 12 Prince Georges Park, 118411, Singapore
Xiaobo Chen*
Affiliation:
Research Department, Bureau Veritas, 8 Cours du Triangle, Paris La Defense, 92937, France College of Shipbuilding Engineering, Harbin Engineering University, Harbin, 150001, China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The fundamental solution to steady ship waves accounting for viscous effects (the viscous-ship-wave Green function) is investigated within the framework of the weakly damped free-surface flow theory. An explicit expression of the viscous-ship-wave Green function is firstly derived, and an accurate and efficient technique is described to evaluate the Green function via decomposing the free-surface term into the local-flow component and wave component. To delve into the physical features of the viscous-ship-wave Green function, the asymptotic approximations in the far field due to Kelvin, Havelock and Peters are presented for the flow-field point located inside, at and outside the Kelvin wedge. In addition, uniform approximations to the wave component based on the Chester–Friedman–Ursell (CFU) approximation and the Kelvin–Havelock–Peters (KHP) approximation are carried out. Both numerical evaluation and asymptotic approximations show that the singular behaviour is eliminated and the divergent waves associated with large wavenumbers leading to rapid oscillations are severely damped when viscous effects are accounted for. In addition, viscous effects also alter the apparent wake angle associated with the wave pattern created by a high-speed translating source, and the apparent wake angle is dependent on both 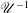$\mathscr{U}^{-1}$ and 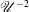$\mathscr{U}^{-2}$, where $\mathscr{U}$ is the translating speed of the source.

JFM classification

Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 744 - 774
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables. National Bureau of Standards.Google Scholar
Benzaquen, M., Darmon, A. & Raphaël, E. 2014 Wake pattern and wave resistance for anisotropic moving disturbances. Phys. Fluids 26 (9), 092106.10.1063/1.4896257Google Scholar
Brard, R. 1972 The representation of a given ship form by singularity distributions when the boundary condition on the free surface is linearized. J. Ship Res. 16 (1), 79–92.10.5957/jsr.1972.16.1.79Google Scholar
Bronshtein, I. N., Semendyayev, K. A., Musiol, G. & Muehlig, H. 2003 Handbook of Mathematics. Springer.Google Scholar
Chen, X. & Wu, G. X. 2001 On singular and highly oscillatory properties of the Green function for ship motions. J. Fluid Mech. 445 (1), 77–91.10.1017/S0022112001005481Google Scholar
Chester, C., Friedman, B. & Ursell, F. 1957 An extension of the method of steepest descents. Math. Proc. Camb. Phil. Soc. 53 (3), 599–611.10.1017/S0305004100032655Google Scholar
Clarisse, J. M. & Newman, J. N. 1994 Evaluation of the wave-resistance Green function. III: the single integral near the singular axis. J. Ship Res. 38 (1), 1–8.10.5957/jsr.1994.38.1.1Google Scholar
Cumberbatch, E. 1965 Effects of viscosity on ship waves. J. Fluid Mech. 23 (3), 471–479.10.1017/S0022112065001490Google Scholar
Dai, Y. Z. 2014 On the interfacial viscous ship waves pattern. In Proceeding of the 29th International Workshop on Water Waves and Floating Bodies, Osaka, Japan (ed. Kashiwagi, M.), pp. 25–28.Google Scholar
Darmon, A., Benzaquen, M. & Raphaël, E. 2014 Kelvin wake pattern at large Froude numbers. J. Fluid Mech. 738, R3.10.1017/jfm.2013.607Google Scholar
Dias, F. 2014 Ship waves and Kelvin. J. Fluid Mech. 746, 1–4.10.1017/jfm.2014.69Google Scholar
Dias, F., Dyachenko, A. I. & Zakharov, V. E. 2008 Theory of weakly damped free-surface flows: a new formulation based on potential flow solutions. Phys. Lett. A 372 (8), 1297–1302.10.1016/j.physleta.2007.09.027Google Scholar
Dutykh, D. & Dias, F. 2007 Viscous potential free-surface flows in a fluid layer of finite depth. C. R. Mathematique 345 (2), 113–118.10.1016/j.crma.2007.06.007Google Scholar
Ellingsen, S. Å. 2014 Ship waves in the presence of uniform vorticity. J. Fluid Mech. 742, R2.10.1017/jfm.2014.28Google Scholar
Forbes, L. K. 1989 An algorithm for 3-dimensional free-surface problems in hydrodynamics. J. Comput. Phys. 82 (2), 330–347.10.1016/0021-9991(89)90052-1Google Scholar
Grue, J. 2017 Ship generated mini-tsunamis. J. Fluid Mech. 816, 142–166.10.1017/jfm.2017.67Google Scholar
Guével, P., Vaussy, P. & Kobus, J. M. 1974 The distribution of singularities kinematically equivalent to a moving hull in the presence of a free surface. Intl Shipbuild. Prog. 21 (243), 311–324.10.3233/ISP-1974-2124301Google Scholar
Havelock, T. H. 1908 The propagation of groups of waves in dispersive media, with application to waves on water produced by a travelling disturbance. Proc. R. Soc. Lond. A 81 (549), 398–430.Google Scholar
Horsley, D. E. & Forbes, L. K. 2013 A spectral method for Faraday waves in rectangular tanks. J. Engng Maths 79 (1), 13–33.10.1007/s10665-012-9562-0Google Scholar
Joseph, D. D. 2003 Viscous potential flow. J. Fluid Mech. 479, 191–197.10.1017/S0022112002003634Google Scholar
Joseph, D. D. & Wang, J. 2004 The dissipation approximation and viscous potential flow. J. Fluid Mech. 505, 365–377.10.1017/S0022112004008602Google Scholar
Kelvin, L. 1887 On the waves produced by a single impulse in water of any depth, or in a dispersive medium. Proc. R. Soc. Lond. A 42 (251–257), 80–83.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Li, Y. & Ellingsen, S. Å. 2016 Ship waves on uniform shear current at finite depth: wave resistance and critical velocity. J. Fluid Mech. 791, 539–567.10.1017/jfm.2016.20Google Scholar
Liang, H. & Chen, X. 2017 Capillary-gravity ship wave patterns. J. Hydrodyn. 29 (5), 825–830.10.1016/S1001-6058(16)60794-1Google Scholar
Liang, H. & Chen, X. 2018 Asymptotic analysis of capillary-gravity waves generated by a moving disturbance. Eur. J. Mech. (B/Fluids) 72, 624–630.10.1016/j.euromechflu.2018.08.012Google Scholar
Liang, H., Wu, H., He, J. & Noblesse, F. 2020 Kelvin–Havelock–Peters approximations to a classical generic wave integral. Appl. Math. Model. 77, 950–962.10.1016/j.apm.2019.08.007Google Scholar
Lighthill, M. J. 1960 Studies on magneto-hydrodynamic waves and other anisotropic wave motions. Phil. Trans. A Math. Phys. Engng Sci. 252, 397–430.Google Scholar
Lighthill, M. J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Longuet-Higgins, M. S. 1992 Theory of weakly damped Stokes waves: a new formulation and its physical interpretation. J. Fluid Mech. 235, 319–324.10.1017/S0022112092001125Google Scholar
Lu, D.-Q. & Chwang, A. T. 2005 Interfacial waves due to a singularity in a system of two semi-infinite fluids. Phys. Fluids 17 (10), 102107.10.1063/1.2120447Google Scholar
Lu, D.-Q. & Chwang, A. T. 2007 Interfacial viscous ship waves near the cusp lines. Wave Motion 44 (7–8), 563–572.10.1016/j.wavemoti.2007.03.002Google Scholar
Lustri, C. J. & Chapman, S. J. 2013 Steady gravity waves due to a submerged source. J. Fluid Mech. 732, 660–686.10.1017/jfm.2013.425Google Scholar
Miao, S. & Liu, Y. 2015 Wave pattern in the wake of an arbitrary moving surface pressure disturbance. Phys. Fluids 27 (12), 122102.10.1063/1.4935961Google Scholar
Moisy, F. & Rabaud, M. 2014 Mach-like capillary-gravity wakes. Phys. Rev. E 90 (2), 023009.Google Scholar
Motygin, O. V. 2017 Numerical approximation of oscillatory integrals of the linear ship wave theory. Appl. Numer. Maths 115, 99–113.10.1016/j.apnum.2017.01.003Google Scholar
Newman, J. N. 1987 Evaluation of the wave-resistance Green function. I: the double integral. J. Ship Res. 31 (2), 79–90.10.5957/jsr.1987.31.2.79Google Scholar
Noblesse, F. 1977 The fundamental solution in the theory of steady motion of a ship. J. Ship Res. 21 (2), 82–88.10.5957/jsr.1977.21.2.82Google Scholar
Noblesse, F. 1981 Alternative integral representations for the Green function of the theory of ship wave resistance. J. Engng Maths 15 (4), 241–265.10.1007/BF00042923Google Scholar
Noblesse, F., Delhommeau, G., Huang, F. & Yang, C. 2011 Practical mathematical representation of the flow due to a distribution of sources on a steadily advancing ship hull. J. Engng Maths 71 (4), 367–392.10.1007/s10665-011-9453-9Google Scholar
Noblesse, F., He, J., Zhu, Y., Hong, L., Zhang, C., Zhu, R. & Yang, C. 2014 Why can ship wakes appear narrower than Kelvin’s angle? Eur. J. Mech. (B/Fluids) 46, 164–171.10.1016/j.euromechflu.2014.03.012Google Scholar
Noblesse, F., Huang, F. & Yang, C. 2013 The Neumann–Michell theory of ship waves. J. Engng Maths 79 (1), 51–71.10.1007/s10665-012-9568-7Google Scholar
Peters, A. S. 1949 A new treatment of the ship wave problem. Commun. Pure Appl. Maths 2 (2–3), 123–148.10.1002/cpa.3160020202Google Scholar
Pethiyagoda, R., McCue, S. W. & Moroney, T. J. 2014a What is the apparent angle of a Kelvin ship wave pattern? J. Fluid Mech. 758, 468–485.10.1017/jfm.2014.530Google Scholar
Pethiyagoda, R., McCue, S. W., Moroney, T. J. & Back, J. M. 2014b Jacobian-free Newton–Krylov methods with GPU acceleration for computing nonlinear ship wave patterns. J. Comput. Phys. 269, 297–313.10.1016/j.jcp.2014.03.024Google Scholar
Rabaud, M. & Moisy, F. 2013 Ship wakes: Kelvin or Mach angle? Phys. Rev. Lett. 110 (21), 214503.10.1103/PhysRevLett.110.214503Google Scholar
Ursell, F. 1960 On Kelvin’s ship-wave pattern. J. Fluid Mech. 8 (03), 418–431.10.1017/S0022112060000700Google Scholar
Wehausen, J. V. 1973 The wave resistance of ships. Adv. Appl. Mech. 13, 93–245.10.1016/S0065-2156(08)70144-3Google Scholar
Wehausen, J. V. & Laitone, E. V. 1960 Surface waves. Hanbuch der Physik 9, 446–778.Google Scholar
Wong, R. 1989 Asymptotic Approximations of Integrals. Academic Press.Google Scholar
Wu, H., He, J., Liang, H. & Noblesse, F. 2019 Influence of Froude number and submergence depth on wave patterns. Eur. J. Mech. (B/Fluids) 75, 258–270.10.1016/j.euromechflu.2018.10.018Google Scholar
Wu, H., He, J., Zhu, Y. & Noblesse, F. 2018 The Kelvin–Havelock–Peters farfield approximation to ship waves. Eur. J. Mech. (B/Fluids) 70, 93–101.10.1016/j.euromechflu.2018.03.004Google Scholar