No CrossRef data available.
Published online by Cambridge University Press: 27 August 2024
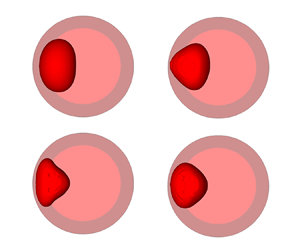
This work is devoted to a theoretical and numerical study of the dynamics of a two-phase system vapour bubble in equilibrium with its liquid phase under translational vibrations in the absence of gravity. The bubble is initially located in the container centre. The liquid and vapour phases are considered as viscous and incompressible. Analysis focuses on the vibrational conditions used in experiments with the two-phase system SF $_6$ in the MIR space station and with the two-phase system para-Hydrogen (p-H
$_6$ in the MIR space station and with the two-phase system para-Hydrogen (p-H $_2$) under magnetic compensation of Earth's gravity. These conditions correspond to small-amplitude high-frequency vibrations. Under vibrations, additionally to the forced oscillations, an average displacement of the bubble to the wall is observed due to an average vibrational attraction force related to the Bernoulli effect. Vibrational conditions for SF
$_2$) under magnetic compensation of Earth's gravity. These conditions correspond to small-amplitude high-frequency vibrations. Under vibrations, additionally to the forced oscillations, an average displacement of the bubble to the wall is observed due to an average vibrational attraction force related to the Bernoulli effect. Vibrational conditions for SF $_6$ correspond to much smaller average vibrational force (weak vibrations) than for p-H
$_6$ correspond to much smaller average vibrational force (weak vibrations) than for p-H $_2$ (strong vibrations). For weak vibrations, the role of the initial vibration phase is crucial. The difference in the behaviour at different initial phases is explained using a simple mechanical model. For strong vibrations, the average displacement to the wall stops when the bubble reaches a quasi-equilibrium position where the resulting average force is zero. At large vibration velocity amplitudes this position is near the wall where the bubble performs only forced oscillations. At moderate vibration velocity amplitudes the bubble average displacement stops at a finite distance from the wall, then large-scale damped oscillations around this position accompanied by forced oscillations are observed. Bubble shape oscillations and the parametric resonance of forced oscillations are also studied.
$_2$ (strong vibrations). For weak vibrations, the role of the initial vibration phase is crucial. The difference in the behaviour at different initial phases is explained using a simple mechanical model. For strong vibrations, the average displacement to the wall stops when the bubble reaches a quasi-equilibrium position where the resulting average force is zero. At large vibration velocity amplitudes this position is near the wall where the bubble performs only forced oscillations. At moderate vibration velocity amplitudes the bubble average displacement stops at a finite distance from the wall, then large-scale damped oscillations around this position accompanied by forced oscillations are observed. Bubble shape oscillations and the parametric resonance of forced oscillations are also studied.