Published online by Cambridge University Press: 12 November 2018
Inviscid vortex models have been demonstrated to capture the essential physics of massively separated flows past aerodynamic surfaces, but they become computationally expensive as coherent vortex structures are formed and the wake is developed. In this work, we present a two-dimensional vortex model in which vortex sheets represent shear layers that separate from sharp edges of the body and point vortices represent the rolled-up cores of these shear layers and the other coherent vortices in the wake. We develop a circulation transfer procedure that enables each vortex sheet to feed its circulation into a point vortex instead of rolling up. This procedure reduces the number of computational elements required to capture the dynamics of vortex formation while eliminating the spurious force that manifests when transferring circulation between vortex elements. By tuning the rate at which the vortex sheets are siphoned into the point vortices, we can adjust the balance between the model’s dimensionality and dynamical richness, enabling it to span the entire taxonomy of inviscid vortex models. This hybrid model can capture the development and subsequent shedding of the starting vortices with insignificant wall-clock time and remain sufficiently low-dimensional to simulate long-time-horizon events such as periodic bluff-body shedding. We demonstrate the viability of the method by modelling the impulsive translation of a wing at various fixed angles of attack, pitch-up manoeuvres that linearly increase the angle of attack from 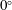 $0^{\circ }$ to
$0^{\circ }$ to 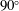 $90^{\circ }$, and oscillatory pitching and heaving. We show that the proposed model correctly predicts the dynamics of large-scale vortical structures in the flow by comparing the distributions of vorticity and force responses from results of the proposed model with a model using only vortex sheets and, in some cases, high-fidelity viscous simulation.
$90^{\circ }$, and oscillatory pitching and heaving. We show that the proposed model correctly predicts the dynamics of large-scale vortical structures in the flow by comparing the distributions of vorticity and force responses from results of the proposed model with a model using only vortex sheets and, in some cases, high-fidelity viscous simulation.