Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T16:40:24.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Velocity–vorticity correlation structure in turbulent channel flow

Published online by Cambridge University Press:  24 February 2014

Jun Chen ,
Fazle Hussain ,
Jie Pei  and
Zhen-Su She
Jun Chen
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, China
Fazle Hussain
Affiliation:
Texas Tech University, Department of Mechanical Engineering, Box 41021, Lubbock, TX 79409-1021, USA
Jie Pei
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, China
Zhen-Su She*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, China
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

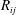A new statistical coherent structure (CS), the velocity–vorticity correlation structure (VVCS), using the two-point cross-correlation coefficient $R_{ij}$ of velocity and vorticity components, 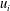$u_i$ and 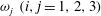$\omega _j~ (i, j = 1, 2, 3)$, is proposed as a useful descriptor of CS. For turbulent channel flow with the wall-normal direction 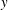$y$, a VVCS study consists of using 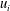$u_i$ at a fixed reference location 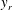$y_r$, and using 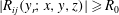$|R_{ij} (y_r; x, y, z)|\geqslant R_0$ to define a topologically invariant high-correlation region, called 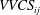$\mathit{VVCS}_{ij}$. The method is applied to direct numerical simulation (DNS) data, and it is shown that the 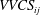$\mathit{VVCS}_{ij}$ qualitatively and quantitatively captures all known geometrical features of near-wall CS, including spanwise spacing, streamwise length and inclination angle of the quasi-streamwise vortices and streaks. A distinct feature of the VVCS is that its geometry continuously varies with 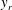$y_r$. A topological change of 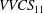$\mathit{VVCS}_{11}$ from quadrupole (for smaller 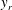$y_r$) to dipole (for larger 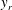$y_r$) occurs at 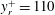$y^{+}_r=110$, giving a geometrical interpretation of the multilayer nature of wall-bounded turbulent shear flows. In conclusion, the VVCS provides a new robust method to quantify CS in wall-bounded flows, and is particularly suitable for extracting statistical geometrical measures using two-point simultaneous data from hotwire, particle image velocimetry/laser Doppler anemometry measurements or DNS/large eddy simulation data.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 291 - 307
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© 2014 Cambridge University Press

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Adrian, R. J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
Antonia, R. A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13, 131–156.Google Scholar
Antonia, R. A. & Kim, J. 1994 Low-Reynolds-number effects on near-wall turbulence. J. Fluid Mech. 276, 61–80.Google Scholar
Asai, M., Minagawa, M. & Nishioka, M. 2002 The instability and breakdown of a near-wall low-speed streak. J. Fluid Mech. 455, 289–314.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. N. 1993 The proper orthogonal decomposition in the analysis of turbuient flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Brooke, J. W. & Hanratty, T. J. 1993 Origin of turbulenceproducing eddies in a channel flow. Phys. Fluids A 5, 1011–1022.Google Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.Google Scholar
Chen, J., Pei, J., She, Z. S. & Hussain, F. 2011 Velocity–vorticity correlation structure in turbulent channel flow. AIP Conf. Proc. 1376 (1), 87–89.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Eckelmann, H., Nychas, S. G., Brodkey, R. S. & Wallace, J. M. 1977 Vorticity and turbulence production in pattern recognized turbulent flow structures. Phys. Fluids 20 (10), S225–S231.Google Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.CrossRefGoogle Scholar
He, L., Yi, S.-H., Zhao, Y.-X., Tian, L.-F. & Chen, Z. 2011 Experimental study of a supersonic turbulent boundary layer using PIV. Sci. China G: Phys., Mech., Astron. 54 (9), 1702–1709.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107 (1981), 297–338.CrossRefGoogle Scholar
Huang, Z.-F., Zhou, H. & Luo, J.-S. 2007 The investigation of coherent structures in the wall region of a supersonic turbulent boundary layer based on DNS database. Sci. China G: Phys., Mech., Astron. 50 (3), 348–356.Google Scholar
Hussain, A. K. M. F. & Hayakawa, M. 1987 Eduction of large-scale organized structures in a turbulent plane wake. J. Fluid Mech. 180, 193–229.Google Scholar
Hussain, A. K. M. F. & Reynolds, W.C. Measurements in fully developed turbulent channel flow. ASME J. Fluids Engng 97, 568–578.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Klewicki, J. C. & Falco, R. E. 1996 Spanwise vorticity structure in turbulent boundary layers. Intl J. Heat Fluid Flow 17, 363–376.Google Scholar
Klewicki, J. C., Murray, J. A. & Falco, R. E. 1994 Vortical motion contributions to stress transport in turbulent boundary layers. Phys. Fluids 6 (1), 277–286.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kreplin, H.-P. & Eckelmann, H. 1979 Propagation of perturbations in the viscous sublayer and adjacent wall region. J. Fluid Mech. 95 (2), 305–322.Google Scholar
Krogstad, P.-Å. & Antonia, R. A. 1994 Structure of turbulent boundary layers on smooth and rough walls. J. Fluid Mech. 277, 1–21.Google Scholar
Li, X., Ma, Y. & Fu, D. 2001 Dns and scaling law analysis of compressible turbulent channel flow. Sci. China Maths 44 (5), 645–654.Google Scholar
Lo, S. H., Voke, P. R. & Rocklife, N. J. 2000 Eddy structures in a simulated low Reynolds number turbulent boundary layer. Flow Turbul. Combust. 64, 1–28.Google Scholar
Pan, C., Wang, J.-J. & Zhang, C. 2009 Identification of Lagrangian coherent structures in the turbuIent boundary layer. Sci. China G: Phys., Mech., Astron. 52 (2), 248–257.Google Scholar
Pei, J., Chen, J., Fazle, H. & She, Z. 2013 New scaling for compressible wall turbulence. Sci. China G Phys., Mech., Astron. 1–12.Google Scholar
Pei, J., Chen, J., She, Z.-S. & Hussain, F. 2012 Model for propagation speed in turbulent channel flows. Phys. Rev. E 86, 046307.CrossRefGoogle ScholarPubMed
Rajagopalan, S. & Antonia, R. A. 1979 Some properties of the large structure in fully developed turbuient duct flow. Phys. Fluids 22 (4), 614–622.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Shadden, S. C., Dabiri, J. O. & Marsden, J. E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18 (4), 047105.Google Scholar
She, Z. S., Chen, X., Wu, Y. & Hussain, F. 2010 New perspective in statistical modeling of wall-bounded turbulence. Acta Mechanica Sin. 26, 847–861.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1970 Entrainment and the structrue of turulent flow. J. Fluid Mech. 41, 13–46.Google Scholar
Wallace, J. M. 2009 Twenty years of experimental and direct numerical simulation access to the velocity gradient tensor: what have we learned about turbulence?. Phys. Fluids 21, 021301.CrossRefGoogle Scholar
Wallace, J. W., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.Google Scholar
Willmarth, W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55 (1), 65–92.Google Scholar
Wu, Y., Chen, X., She, Z.-S. & Hussain, F. 2012 Incorporating boundary constraints to predict mean velocities in turbulent channel flow. Sci. China G: Phys., Mech., Astron. 55 (9), 1691–1695.CrossRefGoogle Scholar
Yang, S.-Q. & Jiang, N. 2012 Tomographic TR-PIV measurement of coherent structure spatial topology utilizing an improved quadrant splitting method. Sci. China G: Phys., Mech., Astron. 55 (10), 1863–1872.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar

Chen et al. supplementary movie

The shape change of VVCS11 with yr.

Download Chen et al. supplementary movie(Video)
Video 220.9 KB