Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T13:50:43.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Velocity ratio effect on flow structures of non-parallel planar starting jets in cross-flow

Published online by Cambridge University Press:  09 March 2021

Ben Steinfurth Open the ORCID record for Ben Steinfurth [Opens in a new window]  and
Julien Weiss Open the ORCID record for Julien Weiss [Opens in a new window]
Ben Steinfurth*
Affiliation:
Institute of Aeronautics and Astronautics, Technische Universität Berlin, Marchstr. 12-14, 10587Berlin, Germany
Julien Weiss
Affiliation:
Institute of Aeronautics and Astronautics, Technische Universität Berlin, Marchstr. 12-14, 10587Berlin, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

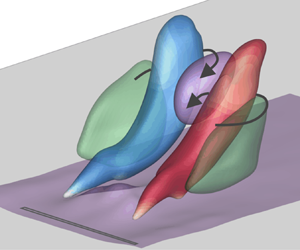
The interaction between starting jets and a steady cross-flow with a zero-pressure-gradient, turbulent boundary layer is studied experimentally. A device typically used in flow control applications is employed as jets of compressed air are injected into the cross-flow through a rectangular high-aspect-ratio outlet. Investigating different velocity ratios between starting jets and cross-flow within the interval $r=u_{jet}/U_\infty =2.4, \ldots ,11$, we identify two regimes of different flow structure appearance, transferring the classification map applicable to parallel circular starting jets in cross-flow established by Sau & Mahesh (J. Fluid Mech., vol. 604, 2008, pp. 389–409). At $r<4$, the vorticity associated with the upstream part of the starting jet is cancelled by the cross-flow boundary layer. Hairpin vortices are observed. At $r>4$, the starting jets penetrate through the boundary layer, and vortex rings are generated. They are asymmetric in shape as the windward vortex ring core is thinner due to the interaction with the cross-flow. As the limiting case of zero cross-flow ($r\rightarrow \infty$) is approached, the asymmetry decreases and the formation time corresponding to maximum vortex ring circulation converges to the characteristic value of $t^*\approx 12$ recently determined for this type of non-parallel planar starting jets when emitted into quiescent surroundings (Steinfurth & Weiss, J. Fluid Mech., vol. 903, 2020, A16). The findings presented in the current article can promote the sophisticated selection of actuation parameters in active mixing and separation control.

JFM classification

Flow Control: Mixing enhancement Vortex Flows: Vortex dynamics Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A11
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afanasyev, Y.D. 2006 Formation of vortex dipoles. Phys. Fluids 18 (3), 037103.CrossRefGoogle Scholar
Bidan, G. & Nikitopoulos, D.E. 2013 On steady and pulsed low-blowing-ratio transverse jets. J. Fluid Mech. 714, 393–433.CrossRefGoogle Scholar
Chang, Y.K. & Vakili, A.D. 1995 Dynamics of vortex rings in crossflow. Phys. Fluids 7 (7), 1583–1597.CrossRefGoogle Scholar
Coulthard, S.M., Volino, R.J. & Flack, K.A. 2006 Effect of jet pulsing on film cooling – Part I: effectiveness and flow-field temperature results. Trans. ASME: J. Turbomach. 129 (2), 232–246.Google Scholar
Coussement, A., Gicquel, O. & Degrez, G. 2012 Large eddy simulation of a pulsed jet in cross-flow. J. Fluid Mech. 695, 1–34.CrossRefGoogle Scholar
Dabiri, J.O. & Gharib, M. 2004 Fluid entrainment by isolated vortex rings. J. Fluid Mech. 511, 311–331.CrossRefGoogle Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30, 101–116.CrossRefGoogle Scholar
Ekkad, S.V., Ou, S. & Rivir, R.B. 2006 Effect of jet pulsation and duty cycle on film cooling from a single jet on a leading edge model. Trans. ASME: J. Turbomach. 128 (3), 564–571.Google Scholar
Eroglu, A. & Breidenthal, R.E. 2001 Structure, penetration, and mixing of pulsed jets in crossflow. AIAA J. 39 (3), 842–850.CrossRefGoogle Scholar
Fernández, J.J.P. & Sesterhenn, J. 2017 Compressible starting jet: pinch-off and vortex ring–trailing jet interaction. J. Fluid Mech. 817, 560–589.CrossRefGoogle Scholar
Fric, T.F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Gordon, M., Cater, J.E. & Soria, J. 2004 Investigation of the mean passive scalar field in zero-net-mass-flux jets in cross-flow using planar-laser-induced fluorescence. Phys. Fluids 16 (3), 794.CrossRefGoogle Scholar
Greenblatt, D. & Wygnanski, I.J. 2000 The control of flow separation by periodic excitation. AIAA J. 36, 487–545.Google Scholar
Hecklau, M., Salazar, D.P. & Nitsche, W. 2010 Influence of the Actuator Jet Angle on the Reattachment Process with Pulsed Excitation. Springer.Google Scholar
Hermanson, J.C., Wahba, A. & Johari, H. 1998 Duty-cycle effects on penetration of fully modulated, turbulent jets in crossflow. AIAA J. 36 (10), 1935–1937.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. In Center for Turbulence Research Report CTR-S88, pp. 193–208.Google Scholar
Hussain, F. & Husain, H.S. 1989 Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 208, 257–320.CrossRefGoogle Scholar
Johari, H. 2006 Scaling of fully pulsed jets in crossflow. AIAA J. 44 (11), 842–850.CrossRefGoogle Scholar
Johari, H., Pacheco-Tougas, M. & Hermanson, J.C. 1999 Penetration and mixing of fully modulated turbulent jets in crossflow. AIAA J. 37 (7), 2719–2725.CrossRefGoogle Scholar
Karagozian, A.R. 2014 The jet in crossflow. Phys. Fluids 26 (10), 101303.CrossRefGoogle Scholar
Krieg, M. & Mohseni, K. 2013 Modelling circulation, impulse and kinetic energy of starting jets with non-zero radial velocity. J. Fluid Mech. 719, 488–526.CrossRefGoogle Scholar
Krueger, P.S. 2005 An over-pressure correction to the slug model for vortex ring circulation. J. Fluid Mech. 545, 427–443.CrossRefGoogle Scholar
Krueger, P.S., Dabiri, J.O. & Gharib, M. 2006 The formation number of vortex rings in uniform background coflow. J. Fluid Mech. 556, 1271–1281.CrossRefGoogle Scholar
Lim, T.T., Lua, K.B. & Thet, K. 2008 Does Kutta lift exist on a vortex ring in a uniform cross flow? Phys. Fluids 20 (5), 051701.CrossRefGoogle Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45, 379–407.CrossRefGoogle Scholar
Margason, R.J. 1993 Fifty years of jet in cross flow research. AGARD CP 538, 15–32.Google Scholar
M'Closkey, R.T., King, J.M., Cortelezzi, L. & Karagozian, A.R. 2002 The actively controlled jet in crossflow. J. Fluid Mech. 452, 325–335.CrossRefGoogle Scholar
Mi, J., Deo, R.C. & Nathan, G.J. 2005 Characterization of turbulent jets from high-aspect-ratio rectangular nozzles. Phys. Fluids 17 (6), 068102.CrossRefGoogle Scholar
Milanovic, I.M. & Zaman, K.B.M.Q. 2005 Synthetic jets in crossflow. AIAA J. 43 (5), 929–940.CrossRefGoogle Scholar
Muldoon, F. & Acharya, S. 2010 Direct numerical simulation of pulsed jets-in-crossflow. Comput. Fluids 39, 1745–1773.CrossRefGoogle Scholar
Norbury, J. 1973 A family of steady vortex rings. J. Fluid Mech. 57 (3), 417–431.CrossRefGoogle Scholar
O'Farrell, C. & Dabiri, J.O. 2014 Pinch-off of non-axisymmetric vortex rings. J. Fluid Mech. 740, 61–96.CrossRefGoogle Scholar
Ostermann, F., Woszidlo, R., Nayeri, C.N. & Paschereit, C.O. 2019 The interaction between a spatially oscillating jet emitted by a fluidic oscillator and a cross-flow. J. Fluid Mech. 863, 215–241.CrossRefGoogle Scholar
Paschereit, C.O., Wygnanski, I. & Fiedler, H.E. 1995 Experimental investigation of subharmonic resonance in an axisymmetric jet. J. Fluid Mech. 283, 365–407.CrossRefGoogle Scholar
Rockwood, M.P., Loiselle, T. & Green, M.A. 2019 Practical concerns of implementing a finite-time Lyapunov exponent analysis with under-resolved data. Exp. Fluids 60, 74.CrossRefGoogle Scholar
Rosenfeld, M., Rambod, E. & Gharib, M. 1998 Circulation and formation number of laminar vortex rings. J. Fluid Mech. 376, 297–318.CrossRefGoogle Scholar
Sau, R. & Mahesh, K. 2007 Passive scalar mixing in vortex rings. J. Fluid Mech. 582, 449–461.CrossRefGoogle Scholar
Sau, R. & Mahesh, K. 2008 Dynamics and mixing of vortex rings in crossflow. J. Fluid Mech. 604, 389–409.CrossRefGoogle Scholar
Smith, S.H. & Mungal, M.G. 1998 Mixing, structure and scaling of the jet in cross-flow. J. Fluid Mech. 357, 83–122.CrossRefGoogle Scholar
Steinfurth, B. & Weiss, J. 2020 a Efficient vortex ring generation with non-parallel planar starting jets in crossflow. In AIAA Scitech 2020 Forum. American Institute of Aeronautics and Astronautics, Inc.CrossRefGoogle Scholar
Steinfurth, B. & Weiss, J. 2020 b Vortex rings produced by non-parallel planar starting jets. J. Fluid Mech. 903, A16.CrossRefGoogle Scholar
Vermeulen, P.J., Odgers, J. & Ramesh, V. 1987 “Full-load” operation of a gas turbine combustor with acoustically controlled dilution-air mixingl. Intl J. Turbo Jet-Engines 4 (1–2), 139–148.CrossRefGoogle Scholar
Westerweel, J. 2008 On velocity gradients in PIV interrogation. Exp. Fluids 44, 831–842.CrossRefGoogle Scholar