Published online by Cambridge University Press: 22 June 2017
This work reports an experimental investigation of the flow through a random array of fixed solid spheres. The volume fraction of the spheres is 2 %, and the Reynolds number
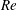 $Re$
based on the sphere diameter and the average flow velocity is varied from 120 to 1040. Using time and spatial averaging, the fluctuations have been decomposed into two contributions of different natures: a spatial fluctuation that accounts for the strong inhomogeneity of the flow around each sphere, and a time fluctuation that comes from the instability of the flow at large enough Reynolds numbers. The evolutions of these two contributions with the Reynolds number are different, so that their relative importance varies. However, when each is normalized by using its own variance and the integral length scales of the fluctuations, their spectra and probability density functions (PDFs) are almost independent of
$Re$
based on the sphere diameter and the average flow velocity is varied from 120 to 1040. Using time and spatial averaging, the fluctuations have been decomposed into two contributions of different natures: a spatial fluctuation that accounts for the strong inhomogeneity of the flow around each sphere, and a time fluctuation that comes from the instability of the flow at large enough Reynolds numbers. The evolutions of these two contributions with the Reynolds number are different, so that their relative importance varies. However, when each is normalized by using its own variance and the integral length scales of the fluctuations, their spectra and probability density functions (PDFs) are almost independent of
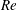 $Re$
. The spatial fluctuation mostly comes from the velocity deficit in the wakes of the spheres, and is thus dominated by scales larger than one or two sphere diameters. It is found to be responsible for the asymmetry of the PDFs of the vertical fluctuations and of the major part of the anisotropy level between the vertical and the horizontal components of the fluctuations. The time fluctuation dominates at scales smaller than the integral length scale. It is isotropic and its PDFs, well described by an exponential distribution, are non-Gaussian. The spectra of the spatial and the time fluctuations both show an evolution as the power
$Re$
. The spatial fluctuation mostly comes from the velocity deficit in the wakes of the spheres, and is thus dominated by scales larger than one or two sphere diameters. It is found to be responsible for the asymmetry of the PDFs of the vertical fluctuations and of the major part of the anisotropy level between the vertical and the horizontal components of the fluctuations. The time fluctuation dominates at scales smaller than the integral length scale. It is isotropic and its PDFs, well described by an exponential distribution, are non-Gaussian. The spectra of the spatial and the time fluctuations both show an evolution as the power
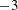 $-3$
of the wavenumber, but not exactly in the same subrange. All these properties are found in remarkable agreement with the results of both experimental investigations and large eddy simulations (LES) of a homogeneous bubble swarm. This confirms that the main mechanism responsible for the production of bubble-induced fluctuations is the interaction of the velocity disturbances caused by obstacles immersed in a flow and that the structure of this agitation is weakly dependent on the precise nature of the obstacles. The understanding and the modelling of the agitation generated by the motion of a dispersed phase, such as the bubble-induced agitation, therefore require one to distinguish between the roles of these two contributions.
$-3$
of the wavenumber, but not exactly in the same subrange. All these properties are found in remarkable agreement with the results of both experimental investigations and large eddy simulations (LES) of a homogeneous bubble swarm. This confirms that the main mechanism responsible for the production of bubble-induced fluctuations is the interaction of the velocity disturbances caused by obstacles immersed in a flow and that the structure of this agitation is weakly dependent on the precise nature of the obstacles. The understanding and the modelling of the agitation generated by the motion of a dispersed phase, such as the bubble-induced agitation, therefore require one to distinguish between the roles of these two contributions.