Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T11:29:48.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Velocity distribution around a sphere descending in a linearly stratified fluid

Published online by Cambridge University Press:  10 August 2017

Shinya Okino Open the ORCID record for Shinya Okino [Opens in a new window] ,
Shinsaku Akiyama  and
Hideshi Hanazaki
Shinya Okino
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto daigaku-katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
Shinsaku Akiyama
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto daigaku-katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
Hideshi Hanazaki*
Affiliation:
Department of Mechanical Engineering and Science, Kyoto University, Kyoto daigaku-katsura 4, Nishikyo-ku, Kyoto 615-8540, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow around a sphere descending at constant speed in a salt-stratified fluid is observed by particle image velocimetry. A unique characteristic of this flow is the appearance of a thin and high-speed rear jet whose maximum velocity can reach more than five times the sphere velocity. 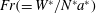In this study we have investigated how the velocity distributions, especially those in the jet and in the boundary layer of the sphere, vary when the Froude number $Fr(=W^{\ast }/N^{\ast }a^{\ast })$ or the Reynolds number 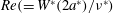$Re(=W^{\ast }(2a^{\ast })/\unicode[STIX]{x1D708}^{\ast })$ (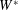$W^{\ast }$: vertical velocity of the sphere, 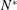$N^{\ast }$: Brunt–Väisälä frequency, 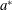$a^{\ast }$: radius of the sphere, $\unicode[STIX]{x1D708}^{\ast }$: kinematic viscosity of the fluid) is changed. The results show that the radius of the jet and the thickness of the boundary layer are comparable, and they decrease for smaller Froude numbers and larger Reynolds numbers. Both of them are estimated at moderate Reynolds numbers by the primitive length scale of the stratified fluid (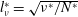$l_{\unicode[STIX]{x1D708}}^{\ast }=\sqrt{\unicode[STIX]{x1D708}^{\ast }/N^{\ast }}$), or in non-dimensional form by 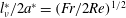$l_{\unicode[STIX]{x1D708}}^{\ast }/2a^{\ast }=(Fr/2Re)^{1/2}$. The overall velocity distribution in the lee of the sphere is measured to identify the internal wave patterns and their effect on the velocity variation along the jet. Corresponding numerical simulation results using the axisymmetry assumption are in agreement with the experimental results.

JFM classification

Geophysical and Geological Flows: Internal waves Wakes/Jets: Jets Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 759 - 780
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abaid, N., Adalsteinsson, D., Agyapong, A. & McLaughlin, R. M. 2004 An internal splash: Levitation of falling spheres in stratified fluids. Phys. Fluids 16, 1567–1580.CrossRefGoogle Scholar
Camassa, R., Falcon, C., Lin, J., McLaughlin, R. M. & Mykins, N. 2010 A first-principle predictive theory for a sphere falling through sharply stratified fluid at low Reynolds number. J. Fluid Mech. 664, 436–465.CrossRefGoogle Scholar
D’Asaro, E. A. 2003 Performance of autonomous Lagrangian floats. J. Atmos. Ocean. Technol. 20, 896–911.Google Scholar
Doostmohammadi, A., Dabiri, S. & Ardekani, A. M. 2014 A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J. Fluid Mech. 750, 5–32.CrossRefGoogle Scholar
Fortuin, J. M. H. 1960 Theory and application of two supplementary methods of constructing density gradient columns. J. Polym. Sci. 44, 505–515.CrossRefGoogle Scholar
Gibson, C. H. 1980 Fossil temperature, salinity, and vorticity turbulence in the ocean. In Marine Turbulence (ed. Nihoul, J.), pp. 221–257. Elsevier.Google Scholar
Hanazaki, H., Kashimoto, K. & Okamura, T. 2009a Jets generated by a sphere moving vertically in a stratified fluid. J. Fluid Mech. 638, 173–197.Google Scholar
Hanazaki, H., Konishi, H. & Okamura, T. 2009b Schmidt-number effects of the flow past a sphere moving vertically in a stratified diffusive fluid. Phys. Fluids 21, 026602.Google Scholar
Hanazaki, H., Nakamura, S. & Yoshikawa, H. 2015 Numerical simulation of jets generated by a sphere moving vertically in a stratified fluid. J. Fluid Mech. 765, 424–451.CrossRefGoogle Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 The internal wave pattern produced by a sphere moving vertically in a density stratified liquid. J. Fluid Mech. 30 (3), 489–495.CrossRefGoogle Scholar
Ochoa, J. L. & Van Woert, M. L.1977 Flow visualization of boundary layer separation in a stratified fluid. Unpublished Report, Scripps Institution of Oceanography 28.Google Scholar
Shanks, A. L. & Trent, J. D. 1980 Marine snow: sinking rate and potential role in vertical flux. Deep-Sea Res. 27, 137–143.CrossRefGoogle Scholar
Srdić-Mitrović, A. N., Mohamed, N. A. & Fernando, H. J. S. 1999 Gravitational settling of particles through density interfaces. J. Fluid Mech. 381, 175–198.Google Scholar
Torres, C. R., Hanazaki, H., Castillo, J. & Van Woert, M. L. 2000 Flow past a sphere moving vertically in a stratified diffusive fluid. J. Fluid Mech. 417, 211–236.Google Scholar
Yick, K. Y., Torres, C. R., Peacock, T. & Stocker, R. 2009 Enhanced drag of a sphere settling in a stratified fluid at small Reynolds numbers. J. Fluid Mech. 632, 49–68.Google Scholar