Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T03:46:44.809Z Has data issue: false hasContentIssue false
  • English
  • Français

The vanishing of strong turbulent fronts in bent pipes

Published online by Cambridge University Press:  13 March 2019

Enrico Rinaldi Open the ORCID record for Enrico Rinaldi [Opens in a new window] ,
Jacopo Canton Open the ORCID record for Jacopo Canton [Opens in a new window]  and
Philipp Schlatter Open the ORCID record for Philipp Schlatter [Opens in a new window]
Enrico Rinaldi
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44, Stockholm, Sweden
Jacopo Canton*
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44, Stockholm, Sweden
Philipp Schlatter
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44, Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Isolated patches of turbulence in transitional straight pipes are sustained by a strong instability at their upstream front, where the production of turbulent kinetic energy (TKE) is up to five times higher than in the core. Direct numerical simulations presented in this paper show no evidence of such strong fronts if the pipe is bent. 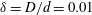We examine the temporal and spatial evolution of puffs and slugs in a toroidal pipe with pipe-to-torus diameter ratio $\unicode[STIX]{x1D6FF}=D/d=0.01$ at several subcritical Reynolds numbers. Results show that the upstream overshoot of TKE production is at most one-and-a-half times the value in the core and that the average cross-flow fluctuations at the front are up to three times lower if compared to a straight pipe, while attaining similar values in the core. Localised turbulence can be sustained at smaller energies through a redistribution of turbulent fluctuations and vortical structures by the in-plane Dean motion of the mean flow. This asymmetry determines a strong localisation of TKE production near the outer bend, where linear and nonlinear mechanisms optimally amplify perturbations. We further observe a substantial reduction of the range of Reynolds numbers for long-lived intermittent turbulence, in agreement with experimental data from the literature. Moreover, no occurrence of nucleation of spots through splitting could be detected in the range of parameters considered. Based on the present results, we argue that this mechanism gradually becomes marginal as the curvature of the pipe increases and the transition scenario approaches a dynamical switch from subcritical to supercritical.

JFM classification

Instability: Nonlinear instability Boundary Layers: Pipe flow boundary layer Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 487 - 502
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.Google Scholar
Barkley, D. 2011 Simplifying the complexity of pipe flow. Phys. Rev. E 84 (1), 016309.Google Scholar
Barkley, D. 2012 Pipe flow as an excitable medium. Rev. Cub. Fis. 29 (1E), 27–30.Google Scholar
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.Google Scholar
Barkley, D., Song, B., Mukund, V., Lemoult, G., Avila, M. & Hof, B. 2015 The rise of fully turbulent flow. Nature 526 (7574), 550–553.Google Scholar
Canton, J.2013 Global linear stability of axisymmetric coaxial jets. Master’s thesis, Politecnico di Milano, Italy.Google Scholar
Canton, J., Örlü, R. & Schlatter, P. 2017 Characterisation of the steady, laminar incompressible flow in toroidal pipes covering the entire curvature range. Intl J. Heat Fluid Flow 66, 95–107.Google Scholar
Canton, J., Schlatter, P. & Örlü, R. 2016 Modal instability of the flow in a toroidal pipe. J. Fluid Mech. 792, 894–909.Google Scholar
Cerbus, R. T., Liu, C.-C., Gioia, G. & Chakraborty, P. 2018 Laws of resistance in transitional pipe flows. Phys. Rev. Lett. 120, 054502.Google Scholar
Cioncolini, A. & Santini, L. 2006 An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 30 (4), 367–380.Google Scholar
Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.Google Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Lond. Edin. Dublin Phil. Mag. J. Sci. 4, 208–223.Google Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2010 Slug genesis in cylindrical pipe flow. J. Fluid Mech. 663, 180–208.Google Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000 web page http://nek5000.mcs.anl.gov.Google Scholar
Foures, D. P. G, Caulfield, C. P. & Schmid, P. J. 2013 Localization of flow sstructure using ∞-norm optimization. J. Fluid Mech. 729, 672–701.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kühnen, J., Braunshier, P., Schwegel, M., Kuhlmann, H. C. & Hof, B. 2015 Subcritical versus supercritical transition to turbulence in curved pipes. J. Fluid Mech. 770, R3.Google Scholar
Kühnen, J., Holzner, M., Hof, B. & Kuhlmann, H. C. 2014 Experimental investigation of transitional flow in a toroidal pipe. J. Fluid Mech. 738, 463–491.Google Scholar
Lindgren, E. R. 1969 Propagation velocity of turbulent slugs and streaks in transition pipe flow. Phys. Fluids 12 (2), 418–425.Google Scholar
Meseguer, Á. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number 107 . J. Comput. Phys. 186 (1), 178–197.Google Scholar
Moxey, D. & Barkley, D. 2010 Distinct large-scale turbulent-laminar states in transitional pipe flow. Proc. Natl Acad. Sci. USA 107 (18), 8091–8096.Google Scholar
Mullin, T. 2011 Experimental studies on transition to turbulence in a pipe. Annu. Rev. Fluid Mech. 43, 1–24.Google Scholar
Nishi, M., Ünsal, B., Durst, F. & Biswas, G. 2008 Laminar-to-turbulent transition of pipe flows through puffs and slugs. J. Fluid Mech. 614, 425–446.Google Scholar
Noorani, A., El Khoury, G. K. & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41, 16–26.Google Scholar
Noorani, A. & Schlatter, P. 2015 Evidence of sublaminar drag naturally occurring in a curved pipe. Phys. Fluids 27 (3), 035105.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.Google Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall he direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. 174, 935–982.Google Scholar
Schanen, M., Marin, O., Zhang, H. & Anitescu, M. 2016 Asynchronous two-level checkpointing scheme for large-scale adjoints in the spectral-element solver Nek5000. Procedia Comput. Sci. 80, 1147–1158.Google Scholar
Shih, H.-Y., Hsieh, T.-L. & Goldenfeld, N. 2015 Ecological collapse and the emergence of travelling waves at the onset of shear turbulence. Nat. Phys. 12, 245–248.Google Scholar
Shimizu, M., Manneville, P., Duguet, Y. & Kawahara, G. 2014 Splitting of a turbulent puff in pipe flow. Fluid Dyn. Res. 46 (6), 061403.Google Scholar
Song, B., Barkley, D., Hof, B. & Avila, M. 2017 Speed and structure of turbulent fronts in pipe flow. J. Fluid Mech. 813, 1045–1059.Google Scholar
Sreenivasan, K. R. & Strykowski, P. J. 1983 Stabilization effects in flow through helically coiled pipes. Exp. Fluids 1 (1), 31–36.Google Scholar
Webster, D. R. & Humphrey, J. A. C. 1993 Experimental observations of flow instability in a helical coil (data bank contribution). Trans. ASME J. Fluids Engng 115 (3), 436–443.Google Scholar
Webster, D. R. & Humphrey, J. A. C. 1997 Traveling wave instability in helical coil flow. Phys. Fluids 9 (2), 407–418.Google Scholar
White, C. M. 1929 Streamline flow through curved pipes. Proc. R. Soc. Lond. A 123 (792), 645–663.Google Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59 (2), 281–335.Google Scholar
Wygnanski, I. J., Sokolov, M. & Friedman, D. 1975 On transition in a pipe. Part 2. The equilibrium puff. J. Fluid Mech. 69 (2), 283–304.Google Scholar

Rinaldi et al. supplementary movie 1

Effect of the secondary motion on the upstream front of a puff.

Download Rinaldi et al. supplementary movie 1(Video)
Video 25.4 MB

Rinaldi et al. supplementary movie 2

Upstream front of a puff in a straight pipe for Re = 2600.

Download Rinaldi et al. supplementary movie 2(Video)
Video 8 MB

Rinaldi et al. supplementary movie 3

Upstream front of a puff in a bent pipe for Re = 3100.

Download Rinaldi et al. supplementary movie 3(Video)
Video 7.4 MB

Rinaldi et al. supplementary movie 4

Upstream front of a puff in a bent pipe for Re = 3300.

Download Rinaldi et al. supplementary movie 4(Video)
Video 11.1 MB

Rinaldi et al. supplementary movie 5

Upstream front of a puff in a bent pipe for Re = 5000.

Download Rinaldi et al. supplementary movie 5(Video)
Video 16.7 MB