Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-07-04T19:09:00.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady two-dimensional jet with flexible flaps at the channel exit

Published online by Cambridge University Press:  26 April 2018

Prashant Das ,
R. N. Govardhan Open the ORCID record for R. N. Govardhan [Opens in a new window]  and
J. H. Arakeri
Prashant Das
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
R. N. Govardhan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
J. H. Arakeri
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present work studies the effect of passive exit flexibility on a two-dimensional starting jet. The exit flexibility is introduced by attaching two flexible (deformable) flaps at the jet exit of a high aspect ratio rectangular duct with the flaps initially being parallel to the channel walls. A controlled piston motion is used to generate the starting jet, which is composed of a rapid acceleration to a constant velocity (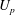$U_{p}$) that is maintained for a given duration of time, after which it is brought to rest impulsively. The parameters which are varied include the flexural rigidity (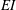$EI$) of the flaps, flap length (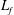$L_{f}$) and piston speed (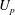$U_{p}$), with measurements of the flap kinematics and flow field in each case. The flaps initially bulge due to the acceleration of the piston from rest, with this bulge growing in size and moving downstream as the flow develops, culminating in a large opening at the flap exit. Subsequently, the flaps return to their initial parallel position and remain there as long as the piston is in motion. Once the piston stops, the flaps collapse inwards due to fluid deceleration causing additional flow out of the flap region in the form of a jet that adds to the net amount of fluid pushed by the piston. We find that the flap kinematics is affected by the flap 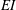$EI$ and 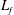$L_{f}$ besides 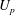$U_{p}$. We define a non-dimensional flexural rigidity 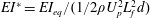$EI^{\ast }=EI_{eq}/(1/2\unicode[STIX]{x1D70C}U_{p}^{2}L_{f}^{2}d)$, where 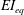$EI_{eq}$ is an equivalent flexural rigidity which takes the self-weight of the flaps into account (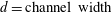$d=\text{channel width}$; 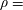$\unicode[STIX]{x1D70C}=$ fluid density). We find that across different 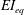$EI_{eq}$, 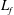$L_{f}$, and piston speeds, the maximum opening of the flap tip and the time taken to reach this maximum opening in terms of 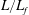$L/L_{f}$ (where 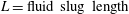$L=\text{fluid slug length}$) fall on a single curve for all the cases studied, when plotted with 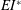$EI^{\ast }$. Particle image velocimetry measurements show that the motion of the flaps results in the formation of additional pairs of vortices when compared to the single vortex pair formed in the absence of flaps. The total final circulation coming out of the flap region remains nearly the same as that of the rigid exit case. However, the final fluid impulse is always found to be higher in the flap cases, with the fluid impulse in most flap cases being approximately two times the fluid impulse of the rigid exit case. This increase in impulse is shown to be linked to the fact that the centroids of vorticity get spread out more in the lateral direction due to the opening of the flaps. The increased impulse and the higher time rate of change of impulse, which is linked with force, suggest that introduction of flexible flaps can help improve thrust performance when looked at from a propulsion point of view.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Wakes/Jets: Jets Biological Fluid Dynamics: Propulsion
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 845 , 25 June 2018 , pp. 462 - 498
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D. 2006 Formation of vortex dipoles. Phys. Fluids 18 (3), 037103.CrossRefGoogle Scholar
Alben, S., Witt, C., Baker, T. V., Anderson, E. & Lauder, G. V. 2012 Dynamics of freely swimming flexible foils. Phys. Fluids 24 (5), 051901.CrossRefGoogle Scholar
Anderson, E. J. & Demont, M. E. 2000 The mechanics of locomotion in the squid Loligo pealei: locomotory function and unsteady hydrodynamics of the jet and intramantle pressure. J. Expl Biol. 203, 2851–2863.CrossRefGoogle ScholarPubMed
Colin, S. P., Costello, J. H., Katija, K., Seymour, J. & Kiefer, K. 2013 Propulsion in cubomedusae: mechanisms and utility. PLoS ONE 8 (2), 1–12.Google ScholarPubMed
Connell, B. S. H. & Yue, D. K. P. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.CrossRefGoogle Scholar
Dabiri, J. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.CrossRefGoogle Scholar
Dabiri, J. O., Colin, S. P. & Costello, J. H. 2006 Fast-swimming hydromedusae exploit velar kinematics to form an optimal vortex wake. J. Expl Biol. 209 (11), 2025–2033.CrossRefGoogle ScholarPubMed
Dabiri, J. O. & Gharib, M. 2005 Starting flow through nozzles with temporally variable exit diameter. J. Fluid Mech. 538, 111–136.CrossRefGoogle Scholar
Dabiri, J. O., Gharib, M., Collin, S. P. & Costello, J. H. 2005 Vortex motion in the ocean: in situ visualization of jellyfish swimming and feeding flows. Phys. Fluids 17 (9), 091108.CrossRefGoogle Scholar
Daniel, T. L. 1983 Mechanics and energetics of medusan jet propulsion. Can. J. Zool. 61 (6), 1406–1420.CrossRefGoogle Scholar
Das, P.2016 Unsteady two dimensional jet with flexible flaps at the exit. PhD thesis, Indian Institute of Science, Bangalore.Google Scholar
Das, P., Govardhan, R. N. & Arakeri, J. H. 2013 Effect of hinged leaflets on vortex pair generation. J. Fluid Mech. 730, 626–658.CrossRefGoogle Scholar
DeVoria, A. C. & Ringuette, M. J. 2013 On the flow generated on the leeward face of a rotating flat plate. Exp. Fluids 54 (4), 1495.Google Scholar
Epps, B. P.2010 An impulse framework for hydrodynamic force analysis: fish propulsion, water entry of spheres, and marine propellers. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Gemmell, B. J., Costello, J. H., Colin, S. P., Stewart, C. J., Dabiri, J. O., Tafti, D. & Priya, S. 2013 Passive energy recapture in jellyfish contributes to propulsive advantage over other metazoans. Proc. Natl Acad. Sci. USA 110 (44), 17904–17909.CrossRefGoogle ScholarPubMed
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Gladfelter, W. G. 1973 A comparative analysis of the locomotory systems of medusoid cnidaria. Helgol. wiss. Meeres. 25 (2), 228–272.CrossRefGoogle Scholar
Katija, K., Colin, S. P., Costello, J. H. & Jiang, H. 2015 Ontogenetic propulsive transitions by Sarsia tubulosa medusae. J. Expl Biol. 218 (15), 2333–2343.Google ScholarPubMed
Kheradvar, A. & Pedrizzetti, G. 2012 Vortex Formation in the Heart, pp. 45–79. Springer.Google Scholar
Kim, D., Hussain, F. & Gharib, M. 2013 Vortex dynamics of clapping plates. J. Fluid Mech. 714, 5–23.CrossRefGoogle Scholar
Kim, W. Y., Walker, P. G., Pedersen, E. M., Poulsen, J. K., Oyre, S., Houlind, K. & Yoganathan, A. P. 1995 Left ventricular blood flow patterns in normal subjects: a quantitative analysis by three-dimensional magnetic resonance velocity mapping. J. Am. Coll. Cardiol. 26 (1), 224–238.CrossRefGoogle ScholarPubMed
Krieg, M. & Mohseni, K. 2013 Modelling circulation, impulse and kinetic energy of starting jets with non-zero radial velocity. J. Fluid Mech. 719, 488–526.CrossRefGoogle Scholar
Krueger, P. 2005 An over-pressure correction to the slug model for vortex ring circulation. J. Fluid Mech. 545, 427–443.CrossRefGoogle Scholar
Krueger, P. S., Dabiri, J. O. & Gharib, M. 2003 Vortex ring pinchoff in the presence of simultaneously initiated uniform background co-flow. Phys. Fluids 15 (7), L49–L52.CrossRefGoogle Scholar
Lee, C. S. F. & Talbot, L. 1979 A fluid-mechanical study of the closure of heart valves. J. Fluid Mech. 91, 41–63.Google Scholar
Lighthill, M. J. 1996 An Informal Introduction to Theoretical Fluid Mechanics. Oxford University Press.Google Scholar
Linden, P. F. & Turner, J. S. 2004 ‘Optimal’ vortex rings and aquatic propulsion mechanisms. Proc. R. Soc. Lond. B 271 (1539), 647–653.CrossRefGoogle ScholarPubMed
Lucas, K. N., Johnson, N., Beaulieu, W. T., Cathcart, E., Tirrell, G., Colin, S. P., Gemmell, B. J., Dabiri, J. O. & Costello, J. H. 2014 Bending rules for animal propulsion. Nat. Commun. 5, 3293.CrossRefGoogle ScholarPubMed
Marais, C., Thiria, B., Wesfreid, J. E. & Godoy-Diana, R. 2012 Stabilizing effect of flexibility in the wake of a flapping foil. J. Fluid Mech. 710, 659–669.CrossRefGoogle Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 Resonance and propulsion performance of a heaving flexible wing. Phys. Fluids 21 (7), 071902.CrossRefGoogle Scholar
Noca, F.1997 On the evaluation of time-dependent fluid-dynamic forces on bluff bodies. PhD thesis, California Institute of Technology.Google Scholar
Pedrizzetti, G. & Domenichini, F. 2015 Left ventricular fluid mechanics: the long way from theoretical models to clinical applications. Ann. Biomed. Engng 43 (1), 26–40.CrossRefGoogle Scholar
Quinn, D. B., Lauder, G. V. & Smits, A. J. 2014a Flexible propulsors in ground effect. Bioinspir. Biomim. 9 (3), 036008.CrossRefGoogle ScholarPubMed
Quinn, D. B., Lauder, G. V. & Smits, A. J. 2014b Scaling the propulsive performance of heaving flexible panels. J. Fluid Mech. 738, 250–267.CrossRefGoogle Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle Image Velocimetry, 2nd edn. Springer.CrossRefGoogle Scholar
Ruiz, L. A., Whittlesey, R. W. & Dabiri, J. O. 2011 Vortex-enhanced propulsion. J. Fluid Mech. 668, 5–32.CrossRefGoogle Scholar
Saffman, P. G. 1993 Vortex Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Sahin, M., Mohseni, K. & Colin, S. P. 2009 The numerical comparison of flow patterns and propulsive performances for the hydromedusae Sarsia tubulosa and Aequorea victoria . J. Expl Biol. 212 (16), 2656–2667.CrossRefGoogle ScholarPubMed
Shelley, M. J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43 (1), 449–465.CrossRefGoogle Scholar
Shinde, S. Y. & Arakeri, J. H. 2014 Flexibility in flapping foil suppresses meandering of induced jet in absence of free stream. J. Fluid Mech. 757, 231–250.CrossRefGoogle Scholar
Shorten, M., Davenport, J., Seymour, J. E., Cross, M. C., Carrette, T. J., Woodward, G. & Cross, T. F. 2005 Kinematic analysis of swimming in Australian box jellyfish, Chiropsalmus sp. and Chironex fleckeri (cubozoa, cnidaria: Chirodropidae). J. Zool. 267 (4), 371–380.CrossRefGoogle Scholar
Shukla, S., Govardhan, R. N. & Arakeri, J. H. 2013 Dynamics of a flexible splitter plate in the wake of a circular cylinder. J. Fluids Struct. 41, 127–134.CrossRefGoogle Scholar
Spagnolie, S. E., Moret, L., Shelley, M. J. & Zhang, J. 2010 Surprising behaviors in flapping locomotion with passive pitching. Phys. Fluids 22 (4).CrossRefGoogle Scholar
Villanueva, A., Vlachos, P. & Priya, S. 2014 Flexible margin kinematics and vortex formation of Aurelia aurita and Robojelly. PLoS ONE 9, e98310.CrossRefGoogle ScholarPubMed
Voropayev, S. I. & Afanasyev, Y. D. 1994 Vortex Structures in a Stratified Fluid. Chapman & Hall.CrossRefGoogle Scholar
Weston, S. P., J. H., Colin, Costello,  & Abbott, E. 2009 Changing form and function during development in rowing hydromedusae. Mar. Ecol. Prog. Series 374, 127–134.CrossRefGoogle Scholar
Whittlesey, R. W. & Dabiri, J. O. 2013 Optimal vortex formation in a self-propelled vehicle. J. Fluid Mech. 737, 78–104.CrossRefGoogle Scholar
Wilson, M. M. & Eldredge, J. D. 2011 Performance improvement through passive mechanics in jellyfish-inspired swimming. Intl J. Non-Linear Mech. 46 (4), 557–567.CrossRefGoogle Scholar