Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T11:26:50.673Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady propulsion by an intermittent swimming gait

Published online by Cambridge University Press:  17 November 2017

Emre Akoz Open the ORCID record for Emre Akoz [Opens in a new window]  and
Keith W. Moored Open the ORCID record for Keith W. Moored [Opens in a new window]
Emre Akoz*
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
Keith W. Moored
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Inviscid computational results are presented on a self-propelled swimmer modelled as a virtual body combined with a two-dimensional hydrofoil pitching intermittently about its leading edge. Lighthill (Proc. R. Soc. Lond. B, vol. 179, 1971, pp. 125–138) originally proposed that this burst-and-coast behaviour can save fish energy during swimming by taking advantage of the viscous Bone–Lighthill boundary layer thinning mechanism. Here, an additional inviscid Garrick mechanism is discovered that allows swimmers to control the ratio of their added-mass thrust-producing forces to their circulatory drag-inducing forces by decreasing their duty cycle, 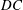$DC$, of locomotion. This mechanism can save intermittent swimmers as much as 60 % of the energy it takes to swim continuously at the same speed. The inviscid energy savings are shown to increase with increasing amplitude of motion, increase with decreasing Lighthill number, 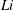$Li$, and switch to an energetic cost above continuous swimming for sufficiently low 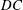$DC$. Intermittent swimmers are observed to shed four vortices per cycle that give rise to an asymmetric time-averaged jet structure with both momentum surplus and deficit branches. In addition, previous thrust and power scaling laws of continuous self-propelled swimming are further generalized to include intermittent swimming. The key is that by averaging the thrust and power coefficients over only the bursting period then the intermittent problem can be transformed into a continuous one. Furthermore, the intermittent thrust and power scaling relations are extended to predict the mean speed and cost of transport of swimmers. By tuning a few coefficients with a handful of simulations these self-propelled relations can become predictive. In the current study, the mean speed and cost of transport are predicted to within 3 % and 18 % of their full-scale values by using these relations.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 834 , 10 January 2018 , pp. 149 - 172
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, E. J., McGillis, W. R. & Grosenbaugh, M. A. 2001 The boundary layer of swimming fish. J. Expl Biol. 204 (1), 81–102.CrossRefGoogle ScholarPubMed
Beamish, H. W. F. 1966 Swimming endurance of some Northwest Atlantic fishes. J. Fisheries Board Canada 23 (3), 341–347.CrossRefGoogle Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Numerical investigation of the hydrodynamics of anguilliform swimming in the transitional and inertial flow regimes. J. Expl Biol. 212 (4), 576–592.CrossRefGoogle ScholarPubMed
Chung, M.-H. 2009 On burst-and-coast swimming performance in fish-like locomotion. Bioinspir. Biomim. 4 (3), 036001.CrossRefGoogle ScholarPubMed
Dewey, P. A., Boschitsch, B. M., Moored, K. W., Stone, H. A. & Smits, A. J. 2013 Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 732, 29–46.CrossRefGoogle Scholar
Ehrenstein, U. & Eloy, C. 2013 Skin friction on a moving wall and its implications for swimming animals. J. Fluid Mech. 718, 321–346.CrossRefGoogle Scholar
Ehrenstein, U., Marquillie, M. & Eloy, C. 2014 Skin friction on a flapping plate in uniform flow. Phil. Trans. R. Soc. Lond. A 372 (2020), 20130345.Google ScholarPubMed
Eloy, C. 2013 On the best design for undulatory swimming. J. Fluid Mech. 717, 48–89.CrossRefGoogle Scholar
Fish, F. E., Schreiber, C., Moored, K. W., Liu, G., Dong, H. & Bart-Smith, H. 2016 Hydrodynamic performance of aquatic flapping: efficiency of underwater flight in the manta. Aerospace 3 (3), 20.CrossRefGoogle Scholar
Garrick, I.1936 Propulsion of a flapping and oscillating airfoil. NACA Tech. Rep. 567.Google Scholar
Gleiss, A. C., Jorgensen, S. J., Liebsch, N., Sala, J. E., Norman, B., Hays, G. C., Quintana, F., Grundy, E., Campagna, C., Trites, A. W. et al. 2011 Convergent evolution in locomotory patterns of flying and swimming animals. Nat. Commun. 2, 352–357.CrossRefGoogle ScholarPubMed
Katz, J. & Plotkin, A. 2001 Low Speed Aerodynamics, 13th edn. Cambridge University Press.CrossRefGoogle Scholar
Kramer, D. L. & McLaughlin, R. L. 2001 The behavioral ecology of intermittent locomotion. Am. Zool. 41 (2), 137–153.Google Scholar
Krasny, R. 1986 A study of singularity formation in a vortex sheet by the point-vortex approximation. J. Fluid Mech. 167, 65–93.CrossRefGoogle Scholar
Lighthill, M. J. 1971 Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179 (1055), 125–138.Google Scholar
Marais, C., Thiria, B., Wesfreid, J. E. & Godoy-Diana, R. 2012 Stabilizing effect of flexibility in the wake of a flapping foil. J. Fluid Mech. 710, 659–669.CrossRefGoogle Scholar
Moore, M. N. J. 2014 Analytical results on the role of flexibility in flapping propulsion. J. Fluid Mech. 757, 599–612.CrossRefGoogle Scholar
Moore, M. N. J. 2015 Torsional spring is the optimal flexibility arrangement for thrust production of a flapping wing. Phys. Fluids 27 (9), 091701.CrossRefGoogle Scholar
Moore, M. N. J. 2017 A fast Chebyshev method for simulating flexible-wing propulsion. J. Comput. Phys. 345, 792–817.CrossRefGoogle Scholar
Moored, K. W.2017 Unsteady three-dimensional boundary element method for self-propelled bio-inspired locomotion. Preprint arXiv:1703.08259.CrossRefGoogle Scholar
Moored, K. W. & Quinn, D. B.2017 Inviscid scaling laws of a self-propelled pitching airfoil. Preprint arXiv:1703.08225.Google Scholar
Müller, U. K., Stamhuis, E. J. & Videler, J. J. 2000 Hydrodynamics of unsteady fish swimming and the effects of body size: comparing the flow fields of fish larvae and adults. J. Expl Biol. 203 (2), 193–206.CrossRefGoogle ScholarPubMed
Munson, B. R., Young, D. F. & Okiishi, T. H. 1990 Fundamentals of Fluid Mechanics. John Wiley & Sons.Google Scholar
Noda, T., Fujioka, K., Fukuda, H., Mitamura, H., Ichikawa, K. & Arai, N. 2016 The influence of body size on the intermittent locomotion of a pelagic schooling fish. Proc. R. Soc. Lond. B 283 (1832), 20153019.Google ScholarPubMed
Quinn, D. B., Moored, K. W., Dewey, P. A. & Smits, A. J. 2014 Unsteady propulsion near a solid boundary. J. Fluid Mech. 742, 152–170.CrossRefGoogle Scholar
Takagi, T., Tamura, Y. & Weihs, D. 2013 Hydrodynamics and energy-saving swimming techniques of Pacific bluefin tuna. J. Theor. Biol. 336, 158–172.CrossRefGoogle ScholarPubMed
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496.Google Scholar
Videler, J. J. 1981 Swimming movements, body structure and propulsion in cod gadus morhua. Symp. Zool. Soc. Lond. 48, 1–27.Google Scholar
Videler, J. J. & Wardle, C. S. 1991 Fish swimming stride by stride: speed limits and endurance. Rev. Fish Biol. Fisheries 1 (1), 23–40.CrossRefGoogle Scholar
Videler, J. J. & Weihs, D. 1982 Energetic advantages of burst-and-coast swimming of fish at high speeds. J. Expl Biol. 97 (1), 169–178.CrossRefGoogle ScholarPubMed
Webb, P. W. 1975 Hydrodynamics and Energetics of Fish Propulsion. Department of the Environment, Canada.Google Scholar
Webb, P. W., Kostecki, P. T. & Stevens, E. D. 1984 The effect of size and swimming speed on locomotor kinematics of rainbow trout. J. Expl Biol. 109 (1), 77–95.CrossRefGoogle Scholar
Webber, D. M., Boutilier, R. G., Kerr, S. R. & Smale, M. J. 2001 Caudal differential pressure as a predictor of swimming speed of cod (Gadus morhua). J. Expl Biol. 204 (20), 3561–3570.CrossRefGoogle ScholarPubMed
Weihs, D. 1974 Energetic advantages of burst swimming of fish. J. Theor. Biol. 48 (1), 215–229.CrossRefGoogle ScholarPubMed
Weihs, D. 1980 Energetic significance of changes in swimming modes during growth of larval anchovy Engraulis mordax. Fishery Bull. 77, 597–604.Google Scholar
Wen, L. & Lauder, G. 2013 Understanding undulatory locomotion in fishes using an inertia-compensated flapping foil robotic device. Bioinspir. Biomim. 8 (4), 046013.CrossRefGoogle ScholarPubMed
Williams, T. M. 2001 Intermittent swimming by mammals: a strategy for increasing energetic. Am. Zool. 176, 166–176.Google Scholar
Wu, G., Yang, Y. & Zeng, L. 2007 Kinematics, hydrodynamics and energetic advantages of burst-and-coast swimming of koi carps (Cyprinus carpio koi). J. Expl Biol. 210 (12), 2181–2191.CrossRefGoogle ScholarPubMed
Yanase, K. & Saarenrinne, P. 2015 Unsteady turbulent boundary layers in swimming rainbow trout. J. Expl Biol. 218 (9), 1373–1385.Google ScholarPubMed
Yanase, K. & Saarenrinne, P. 2016 Boundary layer control by a fish: unsteady laminar boundary layers of rainbow trout swimming in turbulent flows. Biol. Open 5, 1853–1863.CrossRefGoogle ScholarPubMed