Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-09T22:11:50.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady feeding and optimal strokes of model ciliates

Published online by Cambridge University Press:  09 January 2013

Sébastien Michelin  and
Eric Lauga
Sébastien Michelin*
Affiliation:
LadHyX – Département de Mécanique, Ecole polytechnique, 91128 Palaiseau CEDEX, France
Eric Lauga
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0411, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow field created by swimming micro-organisms not only enables their locomotion but also leads to advective transport of nutrients. In this paper we address analytically and computationally the link between unsteady feeding and unsteady swimming on a model micro-organism, the spherical squirmer, actuating the fluid in a time-periodic manner. 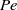We start by performing asymptotic calculations at low Péclet number ($\mathit{Pe}$) on the advection–diffusion problem for the nutrients. We show that the mean rate of feeding as well as its fluctuations in time depend only on the swimming modes of the squirmer up to order 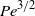${\mathit{Pe}}^{3/ 2} $, even when no swimming occurs on average, while the influence of non-swimming modes comes in only at order 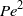${\mathit{Pe}}^{2} $. We also show that generically we expect a phase delay between feeding and swimming of 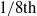$1/ 8\mathrm{th} $ of a period. Numerical computations for illustrative strokes at finite 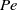$\mathit{Pe}$ confirm quantitatively our analytical results linking swimming and feeding. We finally derive, and use, an adjoint-based optimization algorithm to determine the optimal unsteady strokes maximizing feeding rate for a fixed energy budget. The overall optimal feeder is always the optimal steady swimmer. Within the set of time-periodic strokes, the optimal feeding strokes are found to be equivalent to those optimizing periodic swimming for all values of the Péclet number, and correspond to a regularization of the overall steady optimal.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Low-Reynolds-number flows: Low-Reynolds-number flows Biological Fluid Dynamics: Micro-organism dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 1 - 31
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 4, 387–394.CrossRefGoogle Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.Google Scholar
Berg, H. C. 1993 Random Walks in Biology. Princeton University Press.Google Scholar
Berke, A. P., Turner, L., Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming micoorganisms by surfaces. Phys. Rev. Lett. 101, 038102.Google Scholar
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46, 199–208.Google Scholar
Blake, J. R. & Sleigh, M. A. 1974 Mechanics of ciliary locomotion. Biol. Rev. 49, 85–125.CrossRefGoogle ScholarPubMed
Brennen, C. & Winnet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9, 339–398.Google Scholar
Childress, S., Koehl, M. A. R. & Miksis, M. 1987 Scanning currents in Stokes flow and the feeding of small organisms. J. Fluid Mech. 177, 407–436.Google Scholar
Crawford, D. W. & Purdie, D. A. 1992 Evidence for avoidance of flushing from an estuary by a planktonic, phototrophic ciliate. Mar. Ecol. Prog. Ser. 79, 259–265.Google Scholar
Doostmohammadi, A., Stocker, R. & Ardekani, A. M. 2012 Low-Reynolds-number swimming at pycnoclines. Proc. Natl Acad. Sci. 109, 3856–3861.CrossRefGoogle ScholarPubMed
Drescher, K., Leptos, K. C., Tuval, I., Ishikawa, T., Pedley, T. J. & Goldstein, R. E. 2009 Dancing volvox hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102, 168101.Google Scholar
Evans, A. A., Ishikawa, T., Yamaguchi, T. & Lauga, E. 2011 Orientational order in concentrated suspensions of spherical microswimmers. Phys. Fluids 23, 111702.CrossRefGoogle Scholar
Hamel, A., Fish, C., Combettes, L., Dupuis-Williams, P. & Baroud, C. N. 2011 Transitions between three swimming gaits in Paramecium escape. Proc. Natl Acad. Sci. 108, 7290–7295.Google Scholar
Ishikawa, T. & Pedley, T. J. 2007 Diffusion of swimming model micro-organisms in a semi-dilute suspension. J. Fluid Mech. 588, 437–462.Google Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.CrossRefGoogle Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2007 The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 588, 399–435.Google Scholar
Kessler, J. O. 1986 Individual and collective fluid dynamics of swimming cells. J. Fluid Mech. 173, 191–205.Google Scholar
Kurtuldu, H., Guasto, J. S., Johnson, K. A. & Gollub, J. P. 2011 Enhancement of biomixing by swimming algal cells in two-dimensional films. Proc. Natl Acad. Sci. 108, 10391–10395.Google Scholar
Lauga, E., DiLuzio, W. R., Whitesides, G. M. & Stone, H. A. 2006 Swimming in circles: motion of bacteria near solid boundaries. Biophys. J. 90, 400–412.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming micro-organisms. Rep. Prog. Phys. 72, 096601.Google Scholar
Leptos, K. C., Guasto, J. S., Gollub, J. P., Pesci, A. I. & Goldstein, R. E. 2009 Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 103, 198103.Google Scholar
Leshansky, A. M., Kenneth, O., Gat, O. & Avron, J. E. 2007 A frictionless microswimmer. New J. Phys. 9, 145.Google Scholar
Lighthill, M. J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5, 109–118.CrossRefGoogle Scholar
Lighthill, J. 1975 Mathematical Biofluid-Dynamics. SIAM.CrossRefGoogle Scholar
Lin, Z., Thiffeault, J.-L. & Childress, S. 2011 Stirring by squirmers. J. Fluid Mech. 669, 167–177.CrossRefGoogle Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Appl. Maths 56, 65–91.Google Scholar
Magar, V. & Pedley, T. J. 2005 Average nutrient uptake by a self-propelled unsteady squirmer. J. Fluid Mech. 539, 93–112.Google Scholar
Michelin, S. & Lauga, E. 2010a Efficiency optimization and symmetry-breaking in an envelope model for ciliary locomotion. Phys. Fluids 22, 111901.Google Scholar
Michelin, S. & Lauga, E. 2010b The long-time dynamics of two hydrodynamically-coupled swimming cells. Bull. Math. Biol. 72, 973–1005.Google Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23 (10).Google Scholar
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24, 313–358.Google Scholar
Purcell, E. M. 1977 Life at low-Reynolds number. Am. J. Phys. 45, 3–11.Google Scholar
Saintillan, D. & Shelley, M. J. 2008a Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100, 178103.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008b Instabilities, pattern formation and mixing in active particle suspensions. Phys. Fluids 20, 123304.Google Scholar
Short, M. B., Solari, C. A., Ganguly, S., Powers, T. R., Kessler, J. O. & Goldstein, R. E. 2006 Flows driven by flagella or multicellular organisms enhance long-range molecular transport. Proc. Natl Acad. Sci. 103, 8315–8319.Google Scholar
Sokolov, A., Aranson, I. S., Kessler, J. O. & Goldstein, R. E. 2007 Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 98, 158102.CrossRefGoogle ScholarPubMed
Spagnolie, S. & Lauga, E. 2010 The optimal elastic flagellum. Phys. Fluids 22, 031901.CrossRefGoogle Scholar
Suarez, S. S. & Pacey, A. A. 2006 Sperm transport in the female reproductive tract. Hum. Reprod. Update 12, 23–37.CrossRefGoogle ScholarPubMed
Tam, D. & Hosoi, A. E. 2007 Optimal stroke patterns for Purcell’s three-link swimmer. Phys. Rev. Lett. 98 (6), 068105.CrossRefGoogle ScholarPubMed
Tam, D. & Hosoi, A. E. 2011a Optimal feeding and swimming gaits of biflagellated organisms. Proc. Natl Acad. Sci. 108 (3), 1001.Google Scholar
Tam, D. & Hosoi, A. E. 2011b Optimal kinematics and morphologies for spermatozoa. Phys. Rev. E 83, 045303.Google Scholar