Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-29T16:13:41.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady Coanda effect and drag reduction for a turbulent wake

Published online by Cambridge University Press:  27 July 2020

Yann Haffner Open the ORCID record for Yann Haffner [Opens in a new window] ,
Jacques Borée ,
Andreas Spohn  and
Thomas Castelain
Yann Haffner*
Affiliation:
Institut Pprime, UPR 3346 CNRS, ENSMA, Département Fluides Thermique et Combustion, Université de Poitiers, 86360Futuroscope-Chasseneuil, France
Jacques Borée
Affiliation:
Institut Pprime, UPR 3346 CNRS, ENSMA, Département Fluides Thermique et Combustion, Université de Poitiers, 86360Futuroscope-Chasseneuil, France
Andreas Spohn
Affiliation:
Institut Pprime, UPR 3346 CNRS, ENSMA, Département Fluides Thermique et Combustion, Université de Poitiers, 86360Futuroscope-Chasseneuil, France
Thomas Castelain
Affiliation:
Université de Lyon, Université Claude Bernard Lyon I, Ecole Centrale de Lyon, INSA Lyon, CNRS, LMFA UMR 5509, 69100Villeurbanne, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

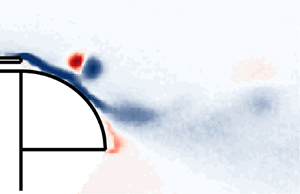
We experimentally study the unsteady forcing of the turbulent wake of a three-dimensional blunt body for drag reduction purposes. The forcing is provided by pulsed jets coupled to small flush-mounted curved surfaces and affects the dynamics of the shear layer at separation from the trailing edge of the model. The systematic analysis of the influence of various parameters (forcing frequency and amplitude, radius of curvature $r$ of the surfaces, free-stream velocity $U_0$) on the base drag reduction provides key ingredients to identify proper scaling laws of the mechanisms involved and to model them. The flow reattachment and separation on the curved surfaces result in a boat-tailing of the wake leading to drag reductions of up to $12\,\%$ and are noticeably influenced by the time scale of unsteadiness of the forcing. For high frequencies of the order of $O(U_0/r)$, strong vortical coherent structures produced by the interaction between the pulsed jets and the separating shear layer promote the interaction of the flow with the curved surfaces. Moreover, the local curvature and pressure gradients across the separating shear layer in the vicinity of flow separation are noticeably modified to result in a further pressure drag reduction for a given forcing amplitude. A simple inviscid-flow model illustrates the peculiar induced effect of these coherent structures on the flow, which explains both the curvature effects leading to additional drag decrease and the saturation in drag decrease for increasing forcing amplitude. The results point to the need for careful combination between forcing frequency and size of the curved surfaces to achieve all the potential in drag reduction of the unsteady Coanda effect. The effort to propose scaling laws and models of the unsteady Coanda effect is a step towards implementing this control strategy at an industrial scale or on different fluid dynamics problems.

JFM classification

Flow Control: Drag reduction Wakes/Jets: Wakes Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , A36
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramson, P., Vukasinovic, B. & Glezer, A. 2011 Direct measurements of controlled aerodynamic forces on a wire-suspended axisymmetric body. Exp. fluids 50, 1711–1725.CrossRefGoogle Scholar
Ahmed, S. R., Ramn, G. & Faltin, G. 1984 Some salient features of the time averaged ground vehicle wake. SAE Tech. Report. No. 840300. Society of Automotive Engineers, Inc.CrossRefGoogle Scholar
Amitay, M. & Glezer, A. 2002 Role of actuation frequency in controlled flow reattachment over a stalled airfoil. AIAA J. 40 (2), 209–216.CrossRefGoogle Scholar
Barros, D., Borée, J., Noack, B. R., Spohn, A. & Ruiz, T. 2016 Bluff body drag manipulation using pulsed jets and Coanda effect. J. Fluid Mech. 805, 422–459.CrossRefGoogle Scholar
Barros, D., Ruiz, T., Borée, J. & Noack, B. R. 2016 Bluff body drag manipulation using pulsed jets and Coanda effect. Intl J Flow Control 805, 422–459.Google Scholar
Berk, T. & Ganapathisubramani, B. 2019 Effects of vortex-induced velocity on the development of a synthetic jet issuing into a turbulent boundary layer. J. Fluid Mech. 870, 651–679.CrossRefGoogle Scholar
Berk, T., Medjoun, T. & Ganapathisubramani, B. 2017 Entrainment effects in periodic forcing of the flow over a backward-facing step. Phys. Rev. Fluids 2 (7), 074605.CrossRefGoogle Scholar
Bonnavion, G. & Cadot, O. 2018 Unstable wake dynamics of rectangular flat-backed bluff bodies with inclination and ground proximity. J. Fluid Mech. 854, 196–232.CrossRefGoogle Scholar
Bonnavion, G. & Cadot, O. 2019 Boat-tail effects on the global wake dynamics of a flat-backed body with rectangular section. J. Fluid Struct. 89, 61–71.CrossRefGoogle Scholar
Bradshaw, P. 1973 Effects of streamline curvature on turbulent flow. Tech. Rep. DTIC Document.Google Scholar
Castelain, T., Michard, M., Szmigiel, M., Chacaton, D. & Juvé, D. 2018 Identification of flow classes in the wake of a simplified truck model depending on the underbody velocity. J. Wind Engng Ind. Aerodyn. 175, 352–363.CrossRefGoogle Scholar
Chaligné, S. 2013 Contrôle du sillage d'un corps non profilé. application expérimentale à une maquette simplifiée de véhicule industriel. PhD thesis, Ecole Centrale de Lyon.Google Scholar
Choi, H., Jeon, W. P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Choi, H., Lee, J. & Park, H. 2014 Aerodynamics of heavy vehicles. Annu. Rev. Fluid Mech. 46, 441–468.CrossRefGoogle Scholar
de la Cruz, J. M. G., Brackston, R. D. & Morrison, J. F. 2017 Adaptive base-flaps under variable cross-wind. SAE Technical Paper.Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.CrossRefGoogle Scholar
Darabi, A. & Wygnanski, I. 2004 a Active management of naturally separated flow over a solid surface. Part 1. The forced reattachment process. J. Fluid Mech. 510, 105–129.CrossRefGoogle Scholar
Darabi, A. & Wygnanski, I. 2004 b Active management of naturally separated flow over a solid surface. Part 2. The separation process. J. Fluid Mech. 510, 131–144.CrossRefGoogle Scholar
Englar, R. J. 2001 Advanced aerodynamic devices to improve the performance, economics, handling and safety of heavy vehicles. SAE Tech. Report. No. 2001-01-2072. Society of Automotive Engineers.CrossRefGoogle Scholar
Freund, J. B. & Mungal, M. G. 1994 Drag and wake modification of axisymmetric bluff bodies using Coanda blowing. J. Aircraft 31 (3), 572–578.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Glezer, A., Amitay, M. & Honohan, A. M. 2005 Aspects of low-and high-frequency actuation for aerodynamic flow control. AIAA J. 43 (7), 1501–1511.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013 a Bi-stability in the wake past parallelepiped bodies with various aspect ratios and wall effects. Phys. Fluids 25 (9), 095103.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013 b Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.CrossRefGoogle Scholar
Grandemange, M., Mary, A., Gohlke, M. & Cadot, O. 2013 c Effect on drag of the flow orientation at the base separation of a simplified blunt road vehicle. Exp. Fluids 54 (5), 1529.CrossRefGoogle Scholar
Greenblatt, D. & Wygnanski, I. J. 2000 The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 36, 487–545.CrossRefGoogle Scholar
Haffner, Y. 2020 Manipulation of three-dimensional turbulent wakes for aerodynamic drag reduction. PhD thesis, Ecole Nationale Supérieure de Mécanique et d'Aérotechnique (ENSMA).Google Scholar
Haffner, Y., Borée, J., Spohn, A. & Castelain, T. 2020 Mechanics of bluff body drag reduction during transient near-wake reversals. J. Fluid Mech. 894, A14.CrossRefGoogle Scholar
Kinsler, L. E., Frey, A. R., Coppens, A. B. & Sanders, J. V. 1999 Fundamentals of Acoustics, 4thedn. Wiley.Google Scholar
Lambert, T. J., Vukasinovic, B. & Glezer, A. 2019 A freely yawing axisymmetric bluff body controlled by near-wake flow coupling. J. Fluid Mech. 863, 1123–1156.CrossRefGoogle Scholar
Li, R., Borée, J., Noack, B. R., Cordier, L. & Harambat, F. 2019 Drag reduction mechanisms of a car model at moderate yaw by bi-frequency forcing. Phys. Rev. Fluids 4 (3), 034604.CrossRefGoogle Scholar
Li, R., Noack, B. R., Cordier, L., Borée, J. & Harambat, F. 2017 Drag reduction of a car model by linear genetic programming control. Exp. Fluids 58 (8), 103.CrossRefGoogle Scholar
Littlewood, R. P. & Passmore, M. A. 2012 Aerodynamic drag reduction of a simplified squareback vehicle using steady blowing. Exp. Fluids 53 (2), 519–529.CrossRefGoogle Scholar
Lorite-Díez, M., Jimenéz-González, J. I., Pastur, L., Martńez-Bazán, C. & Cadot, O. 2020 Experimental analysis of the effect of local base blowing on three-dimensional wake modes. J. Fluid Mech. 883, A53.CrossRefGoogle Scholar
Mair, W. A. 1969 Reduction of base drag by boat-tailed afterbodies in low-speed flow. Aeronaut. Q. 20 (4), 307–320.CrossRefGoogle Scholar
Mariotti, A., Buresti, G., Gaggini, G. & Salvetti, M. V. 2017 Separation control and drag reduction for boat-tailed axisymmetric bodies through contoured transverse grooves. J. Fluid Mech. 832, 514–549.CrossRefGoogle Scholar
Mariotti, A., Buresti, G. & Salvetti, M. V. 2015 Connection between base drag, separating boundary layer characteristics and wake mean recirculation length of an axisymmetric blunt-based body. J. Fluids Struct. 55, 191–203.CrossRefGoogle Scholar
Maull, D. & Hoole, B. 1967 The effect of boat-tailing on the flow round a two-dimensional blunt-based aerofoil at zero incidence. J. R. Aeronaut. Soc. 71 (684), 854–858.CrossRefGoogle Scholar
Oxlade, A. 2013 High-frequency pulsed jet forcing of an axisymmetric bluff body wake. PhD thesis, Imperial College London.Google Scholar
Oxlade, A. R., Morrison, J. F., Qubain, A. & Rigas, G. 2015 High-frequency forcing of a turbulent axisymmetric wake. J. Fluid Mech. 770, 305–318.CrossRefGoogle Scholar
Perry, A. K., Pavia, G. & Passmore, M. 2016 Influence of short rear end tapers on the wake of a simplified square-back vehicle: wake topology and rear drag. Exp. Fluids 57 (11), 169.CrossRefGoogle Scholar
Pfeiffer, J. & King, R. 2018 Robust control of drag and lateral dynamic response for road vehicles exposed to cross-wind gusts. Exp. Fluids 59 (3), 45.CrossRefGoogle Scholar
Pitt Ford, C. W. & Babinsky, H. 2013 Lift and the leading-edge vortex. J. Fluid Mech. 720, 280–313.CrossRefGoogle Scholar
Rinehart, C. S. 2011 Aerodynamic forces induced by controlled transitory flow on a body of revolution. PhD thesis, Georgia Institute of Technology.Google Scholar
Roshko, A. 1993 Free shear layers, base pressure and bluff-body drag. Tech. Rep. DTIC Document.CrossRefGoogle Scholar
Ruiz, T., Sicot, C., Brizzi, L. E., Laumonier, J., Borée, J. & Gervais, Y. 2009 Unsteady near wake of a flat disk normal to a wall. Exp. Fluids 47 (4-5), 637.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Schmidt, H. J., Woszidlo, R., Nayeri, C. N. & Paschereit, C. O. 2015 Drag reduction on a rectangular bluff body with base flaps and fluidic oscillators. Exp. Fluids 56 (7), 151.CrossRefGoogle Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24 (1), 235–279.CrossRefGoogle Scholar
Smith, B. L. & Glezer, A. 2002 Jet vectoring using synthetic jets. J. Fluid Mech. 458, 1–34.CrossRefGoogle Scholar
Spohn, A. & Gilliéron, P. 2002 Flow separations generated by a simplified geometry of an automotive vehicle. In IUTAM Symposium: Unsteady Separated Flows.Google Scholar
Stella, F., Mazellier, N., Joseph, P. & Kourta, A. 2018 Mass entrainment-based model for separating flows. Phys. Rev. Fluids 3 (11), 114702.CrossRefGoogle Scholar
Sychev, V. V., Ruban, A. I., Sychev, V. V. & Korolev, G. L. 1998 Asymptotic Theory of Separated Flows. Cambridge University Press.CrossRefGoogle Scholar
Szmigiel, M. 2017 étude du flux de soubassement sur la dynamique du sillage d'un corps non profilé à culot droit: application du contrôle actif pour la réduction de traînée de véhicule industriel. PhD thesis, Ecole Centrale de Lyon.Google Scholar
Trip, R. & Fransson, J. H. M. 2017 Bluff body boundary-layer modification and its effect on the near-wake topology. Phys. Fluids 29 (9), 095105.CrossRefGoogle Scholar
Van Dyke, M. 1969 Higher-order boundary-layer theory. Annu. Rev. Fluid Mech. 1, 265–292.CrossRefGoogle Scholar
Vukasinovic, B., Rusak, Z. & Glezer, A. 2010 Dissipative small-scale actuation of a turbulent shear layer. J. Fluid Mech. 656, 51–81.CrossRefGoogle Scholar
Waldon, M., Peacock, T., Jacobs, G. B., Helu, M. & Haller, G. 2008 Experimental and numerical investigation of the kinematic theory of unsteady separation. J. Fluid Mech. 611, 1–11.CrossRefGoogle Scholar
Wille, R. & Fernholz, H. 1965 Report on the first European mechanics colloquium, on the Coanda effect. J. Fluid Mech. 23, 801–819.CrossRefGoogle Scholar
Wong, D. T.-M. & Mair, W. A. 1983 Boat-tailed afterbodies of square section as drag-reduction devices. J. Wind Engng Ind. Aerodyn. 611, 1–11.Google Scholar
Zaman, K. B. M. & Hussain, A. K. M. F. 1981 Turbulence suppression in free shear flows by controlled excitation. J. Fluid Mech. 103, 133–159.CrossRefGoogle Scholar
Zhang, B. F., Liu, K., Zhou, Y., To, S. & Tu, J. Y. 2018 Active drag reduction of a high-drag Ahmed body based on steady blowing. J. Fluid Mech. 856, 351–396.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar