Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T09:06:07.713Z Has data issue: false hasContentIssue false
  • English
  • Français

Unstable wake dynamics of rectangular flat-backed bluff bodies with inclination and ground proximity

Published online by Cambridge University Press:  06 September 2018

Guillaume Bonnavion Open the ORCID record for Guillaume Bonnavion [Opens in a new window]  and
Olivier Cadot Open the ORCID record for Olivier Cadot [Opens in a new window]
Guillaume Bonnavion*
Affiliation:
IMSIA, UMR 9219 ENSTA-ParisTech/CNRS/CEA/EDF, Université Paris Saclay, 91120 Palaiseau, France
Olivier Cadot
Affiliation:
School of Engineering, The University of Liverpool, Liverpool L69 3BX, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper investigates experimentally the global wake dynamics of a simplified three-dimensional ground vehicle at a Reynolds number of 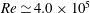$Re\simeq 4.0\times 10^{5}$. The after-body has a blunt rectangular trailing edge leading to a massive flow separation. Both the inclination (yaw and pitch angles) and the distance to the ground (ground clearance) are accurately adjustable. Two different aspect ratios of the rectangular base are considered; wider than it is tall (minor axis perpendicular to the ground) and taller than it is wide (major axis perpendicular to the ground). Measurements of the spatial distribution of the pressure at the base and velocity fields in the wake are used as topological indicators of the flow. Sensitivity analyses of the base pressure gradient expressed in polar form (modulus and phase) varying ground clearance, yaw and pitch are performed. Above a critical ground clearance and whatever the inclination is, the modulus is always found to be large due to the permanent static symmetry-breaking instability, and slightly smaller when aligned with the minor axis of the base rather than when aligned with the major axis. The instability can be characterized with a unique wake mode, quantified by this modulus (asymmetry strength) and a phase (wake orientation) which is the key ingredient of the global wake dynamics. An additional deep rear cavity that suppresses the static instability allows a basic flow to be characterized. It is shown that both the inclination and the ground clearance constrain the phase dynamics of the unstable wake in such way that the component of the pressure gradient aligned with the minor axis of the rectangular base equals that of the basic flow. Meanwhile, the other component related to the major axis adjusts to preserve the large modulus imposed by the instability. In most cases, the dynamics explores only two possible opposite values of the component along the major axis. Their respective probability depends on the geometrical environment of the wake: base shape, body inclination, ground proximity and body supports. An expression for the lateral force coefficients taking into account the wake instability is proposed.

JFM classification

Aerodynamics: Aerodynamics Instability: Instability Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 196 - 232
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, S. R., Ramm, G. & Faitin, G.1984 Some salient features of the time-averaged ground vehicle wake. SAE Tech. Paper Series, 840300.Google Scholar
Barros, D., Borée, J., Cadot, O., Spohn, A. & Noack, B. 2017 Forcing symmetry exchanges and flow reversals in turbulent wakes. J. Fluid Mech. 829, R1.Google Scholar
Barros, D., Borée, J., Noack, B. R., Spohn, A. & Ruiz, T. 2016 Bluff body drag manipulation using pulsed jets and Coanda effect. J. Fluid Mech. 805, 422–459.Google Scholar
Barros, D., Ruiz, T., Borée, J. & Noack, B. R. 2014 Control of three-dimensionnal blunt body wake using low and high frequency pulsed jets. Intl J. Flow Control 6 (1), 61–74.Google Scholar
Bonnavion, G., Cadot, O., Évrard, A., Herbert, V., Parpais, S., Vigneron, R. & Délery, J. 2017 On multistabilities of real car’s wake. J. Wind Engng Ind. Aerodyn. 164, 22–33.Google Scholar
Brackston, R. D., García De La Cruz, J. M., Wynn, A., Rigas, G. & Morrison, J. F. 2016 Stochastic modelling and feedback control of bistability in a turbulent bluff body wake. J. Fluid Mech. 802, 726–749.Google Scholar
Cadot, O. 2016 Stochastic fluid structure interaction of three-dimensional plates facing a uniform flow. J. Fluid Mech. 794, R1.Google Scholar
Cadot, O., Courbois, A., Ricot, D., Ruiz, T., Harambat, F., Herbert, V., Vigneron, R. & Délery, J. 2016 Characterisations of force and pressure fluctuations of real vehicles. Intl J. Engng Syst. Modelling Simul. 8 (2), 99–105.Google Scholar
Cadot, O., Evrard, A. & Pastur, L. 2015 Imperfect supercritical bifurcation in a three-dimensional turbulent wake. Phys. Rev. E 91 (6), 063005.Google Scholar
Castelain, T., Michard, M., Szmigiel, M., Chacaton, D. & Juvé, D. 2018 Identification of flow classes in the wake of a simplified truck model depending on the underbody velocity. J. Wind Engng Ind. Aerodyn. 175, 352–363.Google Scholar
Evrard, A., Cadot, O., Herbert, V., Ricot, D., Vigneron, R. & Délery, J. 2016 Fluid force and symmetry breaking modes of a 3D bluff body with a base cavity. J. Fluids Struct. 61, 99–114.Google Scholar
Evstafyeva, O., Morgans, A. S. & Dalla-Longa, L. 2017 Simulation and feedback control of the Ahmed body flow exhibiting symmetry breaking behaviour. J. Fluid Mech. 817, R2.Google Scholar
Gentile, V., Schrijer, F. F. J., Van Oudheusden, B. W. & Scarano, F. 2016 Low-frequency behavior of the turbulent axisymmetric near-wake. Phys. Fluids 28 (6), 065102.Google Scholar
Gentile, V., Van Oudheusden, B. W., Schrijer, F. F. J. & Scarano, F. 2017 The effect of angular misalignment on low-frequency axisymmetric wake instability. J. Fluid Mech. 813, R3.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2012 Reflectional symmetry breaking of the separated flow over three-dimensional bluff bodies. Phys. Rev. E 86, 035302.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013a Bi-stability in the turbulent wake past parallelepiped bodies with various aspect ratios and wall effects. Phys. Fluids 25, 095103.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013b Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014a Statistical axisymmetry of the turbulent sphere wake. Exp. Fluids 55 (11), 1–10.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014b Turbulent wake past a three-dimensional blunt body. Part 2. Experimental sensitivity analysis. J. Fluid Mech. 752, 439–461.Google Scholar
Hucho, W. H. 1998 Aerodynamics of Road Vehicles. SAE International.Google Scholar
Li, R., Barros, D., Borée, J., Cadot, O., Noack, B. R. & Cordier, L. 2016 Feedback control of bimodal wake dynamics. Exp. Fluids 57 (10), 158.Google Scholar
Lucas, J.-M., Cadot, O., Herbert, V., Parpais, S. & Délery, J. 2017 A numerical investigation of the asymmetric wake mode of a squareback Ahmed body – effect of a base cavity. J. Fluid Mech. 831, 675–697.Google Scholar
McArthur, D., Burton, D., Thompson, M. & Sheridan, J. 2016 On the near wake of a simplified heavy vehicle. J. Fluids Struct. 66, 293–314.Google Scholar
Pasquetti, R. & Peres, N. 2015 A penalty model of synthetic micro-jet actuator with application to the control of wake flows. Comput. Fluids 114 (0), 203–217.Google Scholar
Pavia, G. & Passmore, M. 2018 Characterisation of wake bi-stability for a square-back geometry with rotating wheels. In Progress in Vehicle Aerodynamics and Thermal Management (ed. Wiedemann, J.), pp. 93–109. Springer International Publishing.Google Scholar
Pavia, G., Passmore, M. & Sardu, C. 2018 Evolution of the bi-stable wake of a square-back automotive shape. Exp. Fluids 59 (1), 20.Google Scholar
Perry, A., Almond, M., Passmore, M. & Littlewood, R. 2016a The study of a bi-stable wake region of a generic squareback vehicle using tomographic PIV. SAE Intl J. Passeng. Cars – Mech. Syst 9, 2.Google Scholar
Perry, A., Pavia, G. & Passmore, M. 2016b Influence of short rear end tapers on the wake of a simplified square-back vehicle: wake topology and rear drag. Exp. Fluids 57 (11), 169.Google Scholar
Pier, B. 2008 Local and global instabilities in the wake of a sphere. J. Fluid Mech. 603, 39–61.Google Scholar
Rigas, G., Morgans, A. S., Brackston, R. D. & Morrison, J. F. 2015 Diffusive dynamics and stochastic models of turbulent axisymmetric wakes. J. Fluid Mech. 778, R2.Google Scholar
Rigas, G., Oxlade, A. R., Morgans, A. S. & Morrison, J. F. 2014 Low-dimensional dynamics of a turbulent axisymmetric wake. J. Fluid Mech. 755, R5.Google Scholar
Roshko, A. 1993 Perspectives on bluff body aerodynamics. J. Wind Engng Ind. Aerodyn. 49 (1–3), 79–100.Google Scholar
Schmidt, H.-J., Woszidlo, R., Nayeri, C. N. & Paschereit, C. O. 2018 The effect of flow control on the wake dynamics of a rectangular bluff body in ground proximity. Exp. Fluids 59 (6), 107.Google Scholar
Vilaplana, G., Grandemange, M., Gohlke, M. & Cadot, O. 2013 Experimental sensitivity analysis of the global mode of a sphere turbulent wake using steady disturbances. J. Fluids Struct. 41, 119–126.Google Scholar
Volpe, R., Devinant, P. & Kourta, A. 2015 Experimental characterization of the unsteady natural wake of the full-scale square back Ahmed body: flow bi-stability and spectral analysis. Exp. Fluids 56 (5), 22.Google Scholar

Bonnavion et al. supplementary movie

Instantaneous base pressure distribution~$c_{p}(y^{*},z^{*},t^{*})$ for nose-down, baseline and nose-up configurations corresponding to the time series in figure 6. The signals are low-pass filtered by an averaging on a sliding window of time duration~$t_{w}^{*}=33.3$

Download Bonnavion et al. supplementary movie(Video)
Video 80.9 MB