Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Xue
Chung, Yongmann M.
and
Wan, Minping
2020.
Uniform-momentum zones in a turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Heisel, Michael
de Silva, Charitha M.
Hutchins, Nicholas
Marusic, Ivan
and
Guala, Michele
2020.
On the mixing length eddies and logarithmic mean velocity profile in wall turbulence.
Journal of Fluid Mechanics,
Vol. 887,
Issue. ,
Ebadi, Alireza
Cuevas Bautista, Juan Carlos
White, Christopher M.
Chini, Gregory
and
Klewicki, Joseph
2020.
A heat transfer model of fully developed turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Montemuro, Brandon
White, Christopher M.
Klewicki, Joseph C.
and
Chini, Gregory P.
2020.
A self-sustaining process theory for uniform momentum zones and internal shear layers in high Reynolds number shear flows.
Journal of Fluid Mechanics,
Vol. 901,
Issue. ,
Laskari, Angeliki
and
McKeon, Beverley J.
2021.
Temporal characteristics of the probability density function of velocity in wall-bounded turbulent flows.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Hearst, R. Jason
de Silva, Charitha M.
Dogan, Eda
and
Ganapathisubramani, Bharathram
2021.
Uniform-momentum zones in a turbulent boundary layer subjected to freestream turbulence.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Tang, Zhanqi
Fan, Ziye
Chen, Letian
and
Jiang, Nan
2021.
Outer-layer structure arrangements based on the large-scale zero-crossings at moderate Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 8,
Shrivastava, Shaurya
and
Saxton-Fox, Theresa
2021.
Correlation between Large-Scale Streamwise Velocity Features and the Height of Coherent Vortices in a Turbulent Boundary Layer.
Fluids,
Vol. 6,
Issue. 8,
p.
286.
Anderson, W.
and
Salesky, Scott T.
2021.
Uniform momentum zone scaling arguments from direct numerical simulation of inertia-dominated channel turbulence.
Journal of Fluid Mechanics,
Vol. 906,
Issue. ,
Klewicki, J.C.
2021.
Properties of turbulent channel flow similarity solutions.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Laskari, Angeliki
de Silva, Charitha M.
Hutchins, Nicholas
and
McKeon, Beverley J.
2022.
Spatiotemporal characteristics of uniform momentum zones: Experiments and modeling.
Physical Review Fluids,
Vol. 7,
Issue. 10,
Aksamit, Nikolas O.
and
Haller, George
2022.
Objective momentum barriers in wall turbulence.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Heisel, Michael
de Silva, Charitha M.
Katul, Gabriel G.
and
Chamecki, Marcelo
2022.
Self-similar geometries within the inertial subrange of scales in boundary layer turbulence.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Zheng, Y.
and
Anderson, W.
2022.
Evidence that uniform momentum zones originate from roughness sublayer structure interactions in fully rough channel turbulence.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Heisel, Michael
Sullivan, Peter P.
Katul, Gabriel G.
and
Chamecki, Marcelo
2023.
Turbulence Organization and Mean Profile Shapes in the Stably Stratified Boundary Layer: Zones of Uniform Momentum and Air Temperature.
Boundary-Layer Meteorology,
Vol. 186,
Issue. 3,
p.
533.
Salesky, Scott T.
2023.
Uniform momentum and temperature zones in unstably stratified turbulent flows.
Journal of Fluid Mechanics,
Vol. 958,
Issue. ,
Apostolidis, A.
Laval, J.P.
and
Vassilicos, J.C.
2023.
Turbulent cascade in fully developed turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 967,
Issue. ,
Winiarska, Ewelina
Liberzon, Dan
and
van Hout, René
2024.
Flow Field Characteristics at the Spanwise Edge of a Vegetative Canopy Model.
Boundary-Layer Meteorology,
Vol. 190,
Issue. 10,
Ehsani, Roozbeh
Heisel, Michael
Puccioni, Matteo
Hong, Jiarong
Iungo, Valerio
Voller, Vaughan
and
Guala, Michele
2024.
Stochastic modal velocity field in rough-wall turbulence.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Basse, Nils Tångefjord
2024.
The Chimera Revisited: Wall- and Magnetically-Bounded Turbulent Flows.
Fluids,
Vol. 9,
Issue. 2,
p.
34.
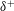 $\unicode[STIX]{x1D6FF}^{+}$ the inertially dominated region of the turbulent boundary layer is composed of large-scale zones of nearly uniform momentum segregated by narrow fissures of concentrated vorticity. Experiments show that, when scaled by the boundary-layer thickness, the fissure thickness is
$\unicode[STIX]{x1D6FF}^{+}$ the inertially dominated region of the turbulent boundary layer is composed of large-scale zones of nearly uniform momentum segregated by narrow fissures of concentrated vorticity. Experiments show that, when scaled by the boundary-layer thickness, the fissure thickness is 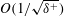 $\mathit{O}(1/\sqrt{\unicode[STIX]{x1D6FF}^{+}})$, while the dimensional jump in streamwise velocity across each fissure scales in proportion to the friction velocity
$\mathit{O}(1/\sqrt{\unicode[STIX]{x1D6FF}^{+}})$, while the dimensional jump in streamwise velocity across each fissure scales in proportion to the friction velocity 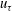 $u_{\unicode[STIX]{x1D70F}}$. A simple model that exploits these essential elements of the turbulent boundary-layer structure at large
$u_{\unicode[STIX]{x1D70F}}$. A simple model that exploits these essential elements of the turbulent boundary-layer structure at large 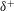 $\unicode[STIX]{x1D6FF}^{+}$ is developed. First, a master wall-normal profile of streamwise velocity is constructed by placing a discrete number of fissures across the boundary layer. The number of fissures and their wall-normal locations follow scalings informed by analysis of the mean momentum equation. The fissures are then randomly displaced in the wall-normal direction, exchanging momentum as they move, to create an instantaneous velocity profile. This process is repeated to generate ensembles of streamwise velocity profiles from which statistical moments are computed. The modelled statistical profiles are shown to agree remarkably well with those acquired from direct numerical simulations of turbulent channel flow at large
$\unicode[STIX]{x1D6FF}^{+}$ is developed. First, a master wall-normal profile of streamwise velocity is constructed by placing a discrete number of fissures across the boundary layer. The number of fissures and their wall-normal locations follow scalings informed by analysis of the mean momentum equation. The fissures are then randomly displaced in the wall-normal direction, exchanging momentum as they move, to create an instantaneous velocity profile. This process is repeated to generate ensembles of streamwise velocity profiles from which statistical moments are computed. The modelled statistical profiles are shown to agree remarkably well with those acquired from direct numerical simulations of turbulent channel flow at large 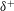 $\unicode[STIX]{x1D6FF}^{+}$. In particular, the model robustly reproduces the empirically observed sub-Gaussian behaviour for the skewness and kurtosis profiles over a large range of input parameters.
$\unicode[STIX]{x1D6FF}^{+}$. In particular, the model robustly reproduces the empirically observed sub-Gaussian behaviour for the skewness and kurtosis profiles over a large range of input parameters.