Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-19T04:03:02.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform momentum zones in turbulent boundary layers

Published online by Cambridge University Press:  02 December 2015

Charitha M. de Silva ,
Nicholas Hutchins  and
Ivan Marusic
Charitha M. de Silva*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

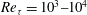Structural properties of regions of uniform streamwise momentum in turbulent boundary layers are examined using experimental databases obtained from particle image velocimetry. This investigation employs a large range of Reynolds numbers, spanning more than an order of magnitude ($Re_{{\it\tau}}=10^{3}{-}10^{4}$), enabling us to provide a detailed description of uniform momentum zones as a function of Reynolds number. Our analysis starts by examining the identification criterion used by Adrian et al. (J. Fluid Mech., vol. 422, 2000, pp. 1–54) to report the presence of uniform momentum zones in turbulent boundary layers. This criterion is then applied to show that a zonal-like structural arrangement is prevalent in all datasets examined, emphasising its importance in the structural organisation. Streamwise velocity fluctuations within the zones are observed to be small but they are bounded by distinct step changes in streamwise momentum which indicate that shear layers of intense vorticity separate each zone. A log-linear increase in the number of these zones with increasing Reynolds number is revealed, together with an increase in the thicknesses of zones with increasing distance from the wall. These results support a hierarchical length-scale distribution of coherent structures, which generate zonal-like organisation within turbulent boundary layers. Interpretation of these findings is aided by employing synthetic velocity fields generated using a model based on the attached eddy hypothesis, which is described in the work of Perry and co-workers. Comparisons between the model and experimental results show that a hierarchy of self-similar structures leads to population densities and length-scale distributions of uniform momentum zones that closely adhere to those observed experimentally in this study.

JFM classification

Boundary Layers: Boundary layer structure Boundary Layers: Boundary Layers Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 786 , 10 January 2016 , pp. 309 - 331
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. S. & Smith, C. R. 1987a A study of hairpin vortices in a laminar boundary. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
Acarlar, M. S. & Smith, C. R. 1987b A study of hairpin vortices in a laminar boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.CrossRefGoogle Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J. & Marusic, I. 2012 Coherent structures in flow over hydraulic engineering surfaces. J. Hydraul Res. 50 (5), 451–464.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Blackwelder, R. F. & Eckelmann, H. 1979 Streamwise vortices associated with the bursting phenomenon. J. Fluid Mech. 94 (03), 577–594.CrossRefGoogle Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Falco, R. E. 1977 Coherent motions in the outer region of turbulent boundary layers. Phys. Fluids 20, S124–S132.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME J. Fluids Engng 132 (9), 094001.Google Scholar
Klewicki, J., Ebner, R. & Wu, X. 2011 Mean dynamics of transitional boundary-layer flow. J. Fluid. Mech. 682, 617–651.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kwon, Y. S., Monty, J. P., Philip, J., de Silva, C. M. & Hutchins, N. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Lee, J., Lee, J. H., Choi, J. & Sung, H. J. 2014 Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13, 735–743.Google Scholar
Marusic, I. 2009 Unravelling turbulence near walls. J. Fluid Mech. 630, 1–4.Google Scholar
Marusic, I. & Adrian, R. J. 2012 The eddies and scales of wall turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Yukio, K. & Sreenivasan, K. R.). Cambridge University Press.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phy. Fluids 7, 694.Google Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 25 (1), 015108.Google Scholar
Na, Y., Hanratty, T. J. & Liu, Z. C. 2001 The use of DNS to define stress producing events for turbulent flow over a smooth wall. Flow Turbul. Combust. 66 (4), 495–512.CrossRefGoogle Scholar
Offen, G. R. & Kline, S. J. 1974 Combined dye-streak and hydrogen-bubble visual observations of a turbulent boundary layer. J. Fluid Mech. 62 (02), 223–239.Google Scholar
Offen, G. R. & Kline, S. J. 1975 A proposed model of the bursting process in turbulent boundary layers. J. Fluid Mech. 70 (02), 209–228.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. M. & Chong, M. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.CrossRefGoogle Scholar
Priyadarshana, P. J. A., Klewicki, J. C., Treat, S. & Foss, J. F. 2007 Statistical structure of turbulent-boundary-layer velocity–vorticity products at high and low Reynolds numbers. J. Fluid Mech. 570, 307–346.Google Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. (B. Fluids) 48, 75–93.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to ${\it\delta}^{+}=2000$ . Phys. Fluids 25 (10), 105102.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014a High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2014b Regions of uniform streamwise momentum in turbulent boundary layers. In 19th Australasian Fluid Mechanics Conference.Google Scholar
de Silva, C. M., Marusic, I., Woodcock, J. D. & Meneveau, C. 2015 Scaling of second- and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.CrossRefGoogle ScholarPubMed
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Theodersen, T. 1952 Mechanism of turbulence. In Proc. Mid-west. Conf. Fluid Mech.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490 (1), 37–74.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent–nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google ScholarPubMed
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally-zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar