Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-04T21:39:30.453Z Has data issue: false hasContentIssue false
  • English
  • Français

Unified theory for a sheared gas–solid suspension: from rapid granular suspension to its small-Stokes-number limit

Published online by Cambridge University Press:  15 May 2019

M. Alam Open the ORCID record for M. Alam [Opens in a new window] ,
S. Saha  and
R. Gupta
M. Alam*
Affiliation:
Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
S. Saha
Affiliation:
Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
R. Gupta
Affiliation:
Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A non-perturbative nonlinear theory for moderately dense gas–solid suspensions is outlined within the framework of the Boltzmann–Enskog equation by extending the work of Saha & Alam (J. Fluid Mech., vol. 833, 2017, pp. 206–246). A linear Stokes’ drag law is adopted for gas–particle interactions, and the viscous dissipation due to hydrodynamic interactions is incorporated in the second-moment equation via a density-corrected Stokes number. 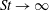For the homogeneous shear flow, the present theory provides a unified treatment of dilute to dense suspensions of highly inelastic particles, encompassing the high-Stokes-number rapid granular regime ($St\rightarrow \infty$) and its small-Stokes-number counterpart, with quantitative agreement for all transport coefficients. It is shown that the predictions of the shear viscosity and normal-stress differences based on existing theories deteriorate markedly with increasing density as well as with decreasing Stokes number and restitution coefficient.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 1175 - 1193
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Saha, S. 2017 Normal stress differences and beyond-Navier–Stokes hydrodynamics. EPJ Conf. Proc. 140, 11014.Google Scholar
Araki, S. & Tremaine, S. 1986 The dynamics of dense particle disks. Icarus 65, 83–109.Google Scholar
Batchelor, G. K. 1970 The stress in a suspension of force-free particles. J. Fluid Mech. 41, 545–577.Google Scholar
Bird, G. A. 1994 Direct Simulation Monte Carlo of Gas Flows. Oxford University Press.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brey, J. J., Dufty, J. W. & Santos, A. 1999 Kinetic models for granular flow. J. Stat. Phys. 97, 281–303.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory for Non-Uniform Gases. Cambridge University Press.Google Scholar
Garzo, V., Tenneti, S., Subramaniam, S. & Hrenya, C. 2012 Enskog kinetic theory for monodisperse gas–solid flows. J. Fluid Mech. 712, 129–168.Google Scholar
Goldreich, P. & Tremaine, S. 1978 The velocity dispersion in Saturn’s rings. Icarus 34, 227–239.Google Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2, 331–407.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.Google Scholar
Guazzelli, E. & Pouliquen, O. 2018 Rheology of dense granular suspensions. J. Fluid Mech. 852, P1.Google Scholar
Gupta, R. & Alam, M. 2017 Hydrodynamics, wall-slip, and normal-stress differences in rarefied granular Poiseuille flow. Phys. Rev. E 95, 022903.Google Scholar
Hinch, E. J. 1977 An averaged-equation approach to particle interactions in a fluid suspension. J. Fluid Mech. 83, 695–720.Google Scholar
Hockling, L. M. 1973 The effect of slip on the motion of a sphere close to a wall and of two adjacent spheres. J. Engng Maths 7, 207–223.Google Scholar
Jackson, R. 2000 Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Jaynes, E. T. 1957 Information theory and statistical mechanics. Phys. Rev. 106, 620–630.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985 Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.Google Scholar
Jenkins, J. T. & Richman, M. W. 1988 Plane simple shear of smooth inelastic circular disks. J. Fluid Mech. 192, 313–328.Google Scholar
Koch, D. L. 1990 Kinetic theory for a monodisperse gas–solid suspension. Phys. Fluids A 2, 1711–1723.Google Scholar
Koch, D. L. & Hill, R. J. 2001 Inertial effects in gas–solid suspension and porous-media flows. Annu. Rev. Fluid Mech. 33, 619–647.Google Scholar
Koch, D. L. & Sangani, A. S. 1999 Particle pressure and marginal stability limits for a homogeneous monodisperse gas-fluidized bed: kinetic theory and numerical simulations. J. Fluid Mech. 400, 229–263.Google Scholar
Kong, B., Fox, R. O., Feng, H., Capecelatro, P. R. & Desjardins, O. 2017 Euler–Euler anisotropic Gaussian mesoscale simulation of homogeneous cluster-induced gas–particle turbulence. AIChE J. 63 (7), 2630–2643.Google Scholar
Lhuillier, D. 2009 Migration of rigid particles in non-Brownian viscous suspensions. Phys. Fluids 21, 023302.Google Scholar
Lun, C. K. K. & Savage, S. B. 2003 Kinetic theory for inertia flows of dilute turbulent gas–solids mixtures. In Granular Gas Dynamics (ed. Pöschel, T. & Brilliantov, N. V.), p. 263. Springer.Google Scholar
Montanero, J. M. & Santos, A. 1997 Viscometric effects in a dense hard-sphere fluid. Physica A 240, 229–238.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.Google Scholar
Nott, P. R., Guazzelli, E. & Pouliquen, O. 2011 The suspension balance model revisited. Phys. Fluids 23, 043304.Google Scholar
Parmentier, J-F. & Simonin, O. 2012 Transition models from the quenched to ignited states for flows of inertial particles suspended in a simple sheared viscous fluid. J. Fluid Mech. 711, 147–160.Google Scholar
Richman, M. W. 1989 The source of second moment in dilute granular flows of highly inelastic spheres. J. Rheol. 33, 1293–1306.Google Scholar
Saha, S. & Alam, M. 2014 Non-Newtonian stress, collisional dissipation and heat flux in the shear flow of inelastic disks: a reduction via Grad’s moment method. J. Fluid Mech. 757, 251–296.Google Scholar
Saha, S. & Alam, M. 2016 Normal stress differences, their origin and constitutive relations for a sheared granular fluid. J. Fluid Mech. 795, 549–580.Google Scholar
Saha, S. & Alam, M. 2017 Revisiting ignited-quenched transition and the non-Newtonian rheology of a sheared dilute gas–solid suspension. J. Fluid Mech. 833, 206–246.Google Scholar
Sangani, A. S., Mo, G., Tsao, H.-K. & Koch, D. L. 1996 Simple shear flows of dense gas–solid suspensions at finite Stokes numbers. J. Fluid Mech. 313, 309–341.Google Scholar
Savage, S. B. & Jeffrey, D. J. 1981 The stress tensor in a granular flow at high shear rates. J. Fluid Mech. 110, 255–272.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–74.Google Scholar
Shukhman, G. 1984 Collisional dynamics of particles in Saturn’s rings. Sov. Astron. 28, 547–584.Google Scholar
Tsao, H.-K. & Koch, D. L. 1995 Simple shear flows of dilute gas–solid suspensions. J. Fluid Mech. 296, 211–246.Google Scholar
Verberg, R. & Koch, D. L. 2006 Rheology of particle suspensions with low to moderate fluid inertia at finite particle inertia. Phys. Fluids 18, 083303.Google Scholar
Vié, A., Doisneau, F. & Massot, M. 2015 On the anisotropic Gaussian velocity closure for inertial-particle laden flow. Commun. Comput. Phys. 17, 1–46.Google Scholar