Published online by Cambridge University Press: 13 December 2017
The evolution of vortex rings in isodensity and isoviscosity fluid has been studied analytically using a novel mathematical model. The model predicts the spatiotemporal variation in peak vorticity, circulation, vortex size and spacing based on instantaneous vortex parameters. This proposed model is quantitatively verified using experimental measurements. Experiments are conducted using high-speed particle image velocimetry (PIV) and laser induced fluorescence (LIF) techniques. Non-buoyant vortex rings are generated from a nozzle using a constant hydrostatic pressure tank. The vortex Reynolds number based on circulation 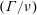 $(\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708})$ is varied in the range 100–1500 to account for a large range of operating conditions. Experimental results show good agreement with theoretical predictions. However, it is observed that neither Saffman’s thin-core model nor the thick-core equations could correctly explain vortex evolution for all initial conditions. Therefore, a transitional theory is framed using force balance equations which seamlessly integrate short- and long-time asymptotic theories. It is found that the parameter
$(\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708})$ is varied in the range 100–1500 to account for a large range of operating conditions. Experimental results show good agreement with theoretical predictions. However, it is observed that neither Saffman’s thin-core model nor the thick-core equations could correctly explain vortex evolution for all initial conditions. Therefore, a transitional theory is framed using force balance equations which seamlessly integrate short- and long-time asymptotic theories. It is found that the parameter 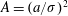 $A=(a/\unicode[STIX]{x1D70E})^{2}$, where
$A=(a/\unicode[STIX]{x1D70E})^{2}$, where  $a$ is the vortex half-spacing and
$a$ is the vortex half-spacing and  $\unicode[STIX]{x1D70E}$ denotes the standard deviation of the Gaussian vorticity profile, governs the regime of vortex evolution. For higher values of
$\unicode[STIX]{x1D70E}$ denotes the standard deviation of the Gaussian vorticity profile, governs the regime of vortex evolution. For higher values of 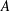 $A$, evolution follows short-time behaviour, while for
$A$, evolution follows short-time behaviour, while for 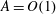 $A=O(1)$, long-time behaviour is prominent. Using this theory, many reported anomalous observations have been explained.
$A=O(1)$, long-time behaviour is prominent. Using this theory, many reported anomalous observations have been explained.