Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T09:17:08.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Uncertainty quantification of unsteady source flows in heterogeneous porous media

Published online by Cambridge University Press:  07 May 2019

Gerardo Severino Open the ORCID record for Gerardo Severino [Opens in a new window] ,
Santolo Leveque  and
Gerardo Toraldo
Gerardo Severino
Affiliation:
Department of Agricultural Sciences, University of Naples – Federico II, I-80055 Portici (NA), Italy
Santolo Leveque
Affiliation:
School of Mathematics, University of Edinburgh, Edinburgh EH8 8FQ, UK
Gerardo Toraldo
Affiliation:
Department of Mathematics and Applications, University of Naples – Federico II, Monte S. Angelo I-80126 Naples, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

Unsteady flow generated by a point-like source takes place into a $d$-dimensional porous formation where the spatial variability of the hydraulic conductivity 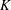$K$ is modelled within a stochastic framework that regards 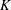$K$ as a stationary, normally distributed random space function (rsf). As a consequence, the hydraulic head 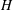$H$ becomes also stochastic, and we aim at quantifying its uncertainty. Towards this aim, we have derived the head covariance by means of a perturbation expansion which regards the variance 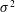$\unicode[STIX]{x1D70E}^{2}$ of the zero mean rsf$\unicode[STIX]{x1D700}=1-K/\langle K\rangle$ (hereafter 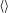$\langle \rangle$ being the ensemble average operator) as a small parameter. The analytical results are expressed in terms of multiple quadratures which are markedly reduced after adopting specific autocorrelation 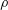$\unicode[STIX]{x1D70C}$ for $\unicode[STIX]{x1D700}$. This enables one to obtain simple results providing straightforward physical insight into the spatial distribution of 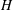$H$ as a consequence of the heterogeneity of 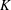$K$. In view of those applications (pumping tests) aiming at the identification of the hydraulic properties of geological formations, we have focused on a flow generated by a source of instantaneous and constant strength. The attainment of the large time (steady-state) regime is studied in detail.

JFM classification

Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 5 - 26
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Division of Water Resources Management and Biosystems Engineering, via Universitá 100, I80055 Portici (NA), Italy. Email address for correspondence: [email protected]

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Dover.Google Scholar
Bruggeman, G. A. 1999 Analytical Solutions of Geohydrological Problems. Elsevier.Google Scholar
Cardiff, M., Barrash, W. & Kitanidis, P. K. 2012 A field proof-of-concept of aquifer imaging using 3-D transient hydraulic tomography with modular, temporarily-emplaced equipment. Water Resour. Res. 48 (5), w05531.Google Scholar
Cardiff, M., Barrash, W. & Kitanidis, P. K. 2013 Hydraulic conductivity imaging from 3-D transient hydraulic tomography at several pumping/observation densities. Water Resour. Res. 49 (11), 7311–7326.Google Scholar
Carslaw, H. S. & Jaeger, J. C. 2000 Conduction of Heat in Solids. Oxford Science Publications.Google Scholar
Cheng, K. B., Rabinovich, A. & Dagan, G. 2019 Stochastic modeling of oscillatory pumping in heterogeneous aquifers with application to Boise aquifer test. J. Hydrol. 569, 278–290.Google Scholar
Choy, T. C. 2015 Effective Medium Theory: Principles and Applications. Oxford University Press.Google Scholar
Crank, J. 2004 The Mathematics of Diffusion. Oxford Science Publications.Google Scholar
Dagan, G. 1982 Stochastic modeling of groundwater flow by unconditional and conditional probabilities: 1. Conditional simulation and the direct problem. Water Resour. Res. 18 (4), 813–833.Google Scholar
Dagan, G. 1984 Solute transport in heterogeneous porous formations. J. Fluid Mech. 145, 151–177.Google Scholar
Dagan, G. 1987 Theory of solute transport by groundwater. Annu. Rev. Fluid Mech. 19 (1), 183–213.Google Scholar
Dagan, G. 1989 Flow and Transport in Porous Formation. Springer.Google Scholar
Dagan, G. & Lessoff, S. C. 2007 Transmissivity upscaling in numerical aquifer models of steady well flow: unconditional statistics. Water Resour. Res. 43 (5), W05431.Google Scholar
Dagan, G. & Rabinovich, A. 2014 Oscillatory pumping wells in phreatic, compressible, and homogeneous aquifers. Water Resour. Res. 50 (8), 7058–7066.Google Scholar
Dagan, G. & Rubin, Y. 1988 Stochastic identification of recharge, transmissivity, and storativity in aquifer transient flow: a quasi-steady approach. Water Resour. Res. 24 (10), 1698–1710.Google Scholar
Fallico, C., De Bartolo, S., Veltri, M. & Severino, G. 2016 On the dependence of the saturated hydraulic conductivity upon the effective porosity through a power law model at different scales. Hydrol. Process. 30 (13), 2366–2372.Google Scholar
Fallico, C., Ianchello, M., De Bartolo, S. & Severino, G. 2018 Spatial dependence of the hydraulic conductivity in a well-type configuration at the mesoscale. Hydrol. Process. 32 (4), 590–595.Google Scholar
Fiori, A. & Jankovic, I. 2012 On preferential flow, channeling and connectivity in heterogeneous porous formations. Math. Geosci. 44 (2), 133–145.Google Scholar
Floryan, J. M. 2015 Flow in a meandering channel. J. Fluid Mech. 770, 52–84.Google Scholar
Gelhar, L. W. 1993 Stochastic Subsurface Hydrology. Prentice Hall.Google Scholar
Gómez, S., Severino, G., Randazzo, L., Toraldo, G. & Otero, J. M. 2009 Identification of the hydraulic conductivity using a global optimization method. Agric. Water Manage. 96 (3), 504–510.Google Scholar
Indelman, P. 1996 Averaging of unsteady flows in heterogeneous media of stationary conductivity. J. Fluid Mech. 310, 39–60.Google Scholar
Indelman, P. 2000 Unsteady source flow in weakly heterogeneous porous media. Comput. Geosci. 4 (4), 351–381.Google Scholar
Indelman, P. 2003 Transient well-type flows in heterogenous formations. Water Resour. Res. 39 (3), 1064.Google Scholar
Jackson, J. D. 2007 Classical Electrodynamics. Wiley.Google Scholar
Jankovic, I., Fiori, A. & Dagan, G. 2003 Effective conductivity of an isotropic heterogeneous medium of lognormal conductivity distribution. Multiscale Model. Simul. 1 (1), 40–56.Google Scholar
Kruseman, G. P. & de Ridder, N. A. 1979 Analysis and Evaluation of Pumping Test Data. International Institute for Land Reclamation and Improvement.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Milne-Thomson, L. M. 1968 Theoretical Hydrodynamics. Courier Corporation.Google Scholar
Neuman, S. P., Tartakovsky, D., Wallstrom, T. C. & Winter, C. L. 1996 Correction to ‘Prediction of steady state flow in nonuniform geologic media by conditional moments: exact nonlocal formalism, effective conductivities, and weak approximation’. Water Resour. Res. 32 (5), 1479–1480.Google Scholar
Pope, S. B. 2010 Turbulent Flows. Cambridge University Press.Google Scholar
Rabinovich, A., Barrash, W., Cardiff, M., Hochstetler, D. L., Bakhos, T., Dagan, G. & Kitanidis, P. K. 2015 Frequency dependent hydraulic properties estimated from oscillatory pumping tests in an unconfined aquifer. J. Hydrol. 531, 2–16.Google Scholar
Riva, M., Guadagnini, A., Neuman, S. P. & Franzetti, S. 2001 Radial flow in a bounded randomly heterogeneous aquifer. Trans. Porous Med. 45 (1), 139–193.Google Scholar
Rubin, Y. 2003 Applied Stochastic Hydrogeology. Oxford University Press.Google Scholar
Rubin, Y. & Dagan, G. 1988 Stochastic analysis of boundaries effects on head spatial variability in heterogeneous aquifers: 1. Constant head boundary. Water Resour. Res. 24 (10), 1689–1697.Google Scholar
Rubin, Y. & Dagan, G. 1989 Stochastic analysis of boundaries effects on head spatial variability in heterogeneous aquifers: 2. Impervious boundary. Water Resour. Res. 25 (4), 707–712.Google Scholar
Saw, E.-W., Debue, P., Kuzzay, D., Daviaud, F. & Dubrulle, B. 2018 On the universality of anomalous scaling exponents of structure functions in turbulent flows. J. Fluid Mech. 837, 657–669.Google Scholar
Severino, G. 2011a Macrodispersion by point-like source flows in randomly heterogeneous porous media. Trans. Porous Med. 89 (1), 121–134.Google Scholar
Severino, G. 2011b Stochastic analysis of well-type flows in randomly heterogeneous porous formations. Water Resour. Res. 47 (3), W03520.Google Scholar
Severino, G. 2019 Effective conductivity in steady well-type flows through porous formations. Stoch. Environ. Res. Risk Assess. 33 (3), 827–835.Google Scholar
Severino, G. & De Bartolo, S. 2015 Stochastic analysis of steady seepage underneath a water-retaining wall through highly anisotropic porous media. J. Fluid Mech. 778, 253–272.Google Scholar
Severino, G., De Bartolo, S., Toraldo, G., Srinivasan, G. & Viswanathan, H. 2012 Travel time approach to kinetically sorbing solute by diverging radial flows through heterogeneous porous formations. Water Resour. Res. 48 (12), W12527.Google Scholar
Severino, G., Monetti, V. M., Santini, A. & Toraldo, G. 2006 Unsaturated transport with linear kinetic sorption under unsteady vertical flow. Trans. Porous Med. 63 (1), 147–174.Google Scholar
Severino, G., Santini, A. & Sommella, A. 2003 Determining the soil hydraulic conductivity by means of a field scale internal drainage. J. Hydrol. 273 (1), 234–248.Google Scholar
Severino, G., Santini, A. & Sommella, A. 2008 Steady flows driven by sources of random strength in heterogeneous aquifers with application to partially penetrating wells. Stoch. Environ. Res. Risk Assess. 22 (4), 567–582.Google Scholar
Severino, G., Santini, A. & Sommella, A. 2011 Macrodispersion by diverging radial flows in randomly heterogeneous porous media. J. Contam. Hydrol. 123 (1), 40–49.Google Scholar
Shvidler, M. I. 1966 The source-type solution in the problem of unsteady filtration in a medium with random nonuniformity. Fluid Dyn. 1 (4), 95–98.Google Scholar
Streltsova, T. D. 1987 Well Testing in Heterogeneous Formations. Wiley.Google Scholar
Tartakovsky, D. M., Guadagnini, A. & Riva, M. 2003 Stochastic averaging of nonlinear flows in heterogeneous porous media. J. Fluid Mech. 492, 47–62.Google Scholar
Tartakovsky, D. M. & Neuman, S. P. 1998a Transient flow in bounded randomly heterogeneous domains: 1. Exact conditional moment equations and recursive approximations. Water Resour. Res. 34 (1), 1–12.Google Scholar
Tartakovsky, D. M. & Neuman, S. P. 1998b Transient flow in bounded randomly heterogeneous domains: 2. Localization of conditional mean equations and temporal nonlocality effects. Water Resour. Res. 34 (1), 13–20.Google Scholar
Wheatcraft, S. W. & Winterberg, F. 1985 Steady state flow passing through a cylinder of permeability different from the surrounding medium. Water Resour. Res. 21 (12), 1923–1929.Google Scholar
Wilczek, M., Stevens, R. J. A. M. & Meneveau, C. 2015 Spatio-temporal spectra in the logarithmic layer of wall turbulence: large-eddy simulations and simple models. J. Fluid Mech. 769, R1.Google Scholar
Ye, M., Neuman, S. P., Guadagnini, A. & Tartakovsky, D. M. 2004 Nonlocal and localized analyses of conditional mean transient flow in bounded, randomly heterogeneous porous media. Water Resour. Res. 40 (5), W05104.Google Scholar
Zhang, D. 2002 Stochastic Methods for Flow in Porous Media. Academic Press.Google Scholar