1. Introduction
The nanoscale pervades a remarkably vast array of fluid flows in nature and industry, encompassing the physicochemical hydrodynamics of biological systems, energy storage, chemical processing, nanotechnology, etc. (Lohse & Zhang Reference Lohse and Zhang2020). The everyday example of drop impact on a solid surface, e.g. the wetting of leaves by raindrops or the jetting of an inkjet printer nozzle, is inherently multiscale even for a ‘simple’ liquid like water, because nanoscale interactions influence the dynamics of the contact line which marks the boundary between liquid, gas and solid (Snoeijer & Andreotti Reference Snoeijer and Andreotti2013).
The rich and beautiful phenomenology of drop impact depends essentially on fluid dynamical parameters – Reynolds and Weber (We) numbers, which are ratios of inertial to viscous and inertial to capillary forces, respectively, and the ratios of liquid–gas densities and viscosities – but also on substrate parameters that emerge from the nanoscale (e.g. wettability, slip length, roughness distribution, etc.) The excellent recent reviews by Josserand & Thoroddsen (Reference Josserand and Thoroddsen2016) and Sprittles (Reference Sprittles2024) discuss the experimental and theoretical state-of-the-art in droplet impact, including the first contact with the substrate during early impact to which Li, Vakarelski & Thoroddsen (Reference Li, Vakarelski and Thoroddsen2015) make pioneering contributions.
Rapid advances in micro- and nano-technology in the past couple of decades have achieved scale reductions which have come to challenge the classical continuum framework of fluid dynamics and led to the emergence of the field of nanofluidics (Bocquet & Charlaix Reference Bocquet and Charlaix2010). It is now well accepted that the continuum framework holds up surprisingly well for bulk flows of simple fluids, with no apparent deviation from the bulk Navier–Stokes equations for confinements <10 nm for liquids, although mean free path estimates indicate that this limit is much increased for gases to  $\sim$100 nm.
$\sim$100 nm.
The quest for the nanoscale has also equipped fluid dynamics with a phenomenal new toolset to resolve the smallest scales in time and space. In addition to ultra-fast direct imaging, examples include the surface force apparatus, which can measure disjoining pressures and their influence on thin film stability and contact-line motion, atomic force microscopy (AFM) for characterisation of substrates, as well as X-ray imaging, high-speed interferometry and total internal reflection which can capture nanoscale-thickness film dynamics.
So how do Li et al. (Reference Li, Vakarelski and Thoroddsen2015) probe the nanoscale in the context of droplet impact? By resolving the impact of a droplet on the hundreds of nanosecond scale to pinpoint the first contact, they are able to explore the role of prescribed nanometre-scale roughness by observing its effect on microscale contact-line dynamics. Hence, more than a century after the beauty and intricacy of splashing during droplet impact on a solid surface was first glimpsed by Worthington (Reference Worthington1876), Li et al. (Reference Li, Vakarelski and Thoroddsen2015) are able to combine 200 ns interframe times with spatial resolution down to the diffraction limit, thanks to the phenomenal advances in imaging technology of the last three decades. Their study was motivated by the recent discovery of the influence of the dynamics of thin gas films on the behaviour of liquid droplets (Xu, Zhang & Nagel Reference Xu, Zhang and Nagel2005). Immediately prior to impact, the lubrication pressure in the gas layer under the drop deforms the underside of the drop into a dimple, so that the first contact occurs along a circle, entrapping a thin gas bubble, which then rapidly contracts to minimise the surface energy. Complementary techniques, including total internal reflection (Kolinski, Mahadevan & Rubinstein Reference Kolinski, Mahadevan and Rubinstein2014) and interferometry (van der Veen et al. Reference van der Veen, Tran, Lohse and Sun2012; de Ruiter et al. Reference de Ruiter, Lagraaw, van den Ende and Mugele2015) have been able to resolve the film trapped between impacting surfaces to broadly reveal two modes of contact on a solid substrate, random contacts through a thin film, associated with prolonged skating for low  $We$, and the outer kink mode for more rapid touchdown at higher We (Sprittles Reference Sprittles2024). The astounding images by Li et al. (Reference Li, Vakarelski and Thoroddsen2015) are a fitting illustration of the hive of activity on droplet impact in the 2010s but also a visual reminder that, however well resolved, yet unexplored nanoscale frontiers remain hidden within these images (see figure 1).
$We$, and the outer kink mode for more rapid touchdown at higher We (Sprittles Reference Sprittles2024). The astounding images by Li et al. (Reference Li, Vakarelski and Thoroddsen2015) are a fitting illustration of the hive of activity on droplet impact in the 2010s but also a visual reminder that, however well resolved, yet unexplored nanoscale frontiers remain hidden within these images (see figure 1).
2. The art of ultra-fast imaging
Entrainment of air can be a limiting factor in industrial applications such as coating and printing, where bubbles degrade the quality and uniformity of the deposited film (Marchand et al. Reference Marchand, Chan, Snoeijer and Andreotti2012). The maximum radius of the entrapped air film during the early contact of an impacting droplet is set by the first contact, and it can be reliably predicted by balancing viscous lubrication in the thin air layer and the rapid deceleration of the drop inertia (Mandre, Mani & Brenner Reference Mandre, Mani and Brenner2009). In fact, the interplay of dynamic wetting and gas films in drop impact routinely leads to entrapment of a small bubble under its centre after retraction of the contact line, but Li et al. (Reference Li, Vakarelski and Thoroddsen2015) also identify the formation of a ring of microbubbles at first contact, due to multiple roughness-induced initial contacts just before the formation of the fully wetted outer section.
Experiments consisted of impacting millimetric water droplets onto three hydrophilic solid substrates, with AFM r.m.s. measures of roughness ranging from 7.3 nm and 1.2 nm for glass to <0.5 nm for freshly cleaved mica. The results are summarised in figure 1. On both types of glass slides (figure 1a,b), microbubbles are left behind at the site of first contact (black arrows) as the newly formed irregular bubbly contact line rapidly contracts into a central bubble. However, the reduction in substrate roughness to 1.2 nm drastically reduces the number of initial contacts so that the volume of air left behind and the irregularity of the contact line are much reduced. The bubbles are now so small that they are difficult to make out individually and the faint trace they leave in the vicinity of the contact line is only visible under suitable magnification and thus, not visible in figure 1(b). This reduction is consistent with the picture that nanobubbles owe their remarkable longevity to pinning of the three-phase contact line at chemical or geometric surface heterogeneities (Lohse & Zhang Reference Lohse and Zhang2015). Now with the mica (figure 1c), the images cannot capture any trace of micro/nanobubbles. Clearly, the molecular smoothness of the cleaved surface suppresses nanobubble formation, possibly compounded by perfect hydrophilicity compared with the small  $20^\circ$ contact angle recorded with cleaned glass. This carries the interesting implication that a mechanism other than roughness acts to rupture the lubricating air film on which the drop initially skates, which Li et al. (Reference Li, Vakarelski and Thoroddsen2015) hypothesise to be van der Waals forces.
$20^\circ$ contact angle recorded with cleaned glass. This carries the interesting implication that a mechanism other than roughness acts to rupture the lubricating air film on which the drop initially skates, which Li et al. (Reference Li, Vakarelski and Thoroddsen2015) hypothesise to be van der Waals forces.
In an effort to investigate a perfectly smooth substrate, Li et al. (Reference Li, Vakarelski and Thoroddsen2015) switch to a millimetric layer of ultra-viscous silicone oil but this radically alters the early contact dynamics. The compliance of the substrate reduces the compression of the gas, enabling more air to be entrapped. Remarkably, microbubbles are again left behind the moving contact line, albeit not from localised contacts due to roughness. Instead, they are formed through the tip streaming of an azimuthal instability of the rapidly moving contact line. The instability wavelength increases linearly with film thickness, thus coarsening the contact-line deformation and increasing the size of the bubbles shed as the gas bubble contracts. Further experimental exploration by Pack et al. (Reference Pack, Kaneelil, Kim and Sun2018) using a high-speed total internal reflection microscopy technique has revealed that this instability is caused by the buildup of the gas pressure near the contact line which can lead to the entrainment of an air rim at the wetting front. Similar ideas may also apply to the small contact-line undulations observed on the low roughness solid substrates (see figure 1b,c), which were broadly assigned to the contact-line dynamics by Li et al. (Reference Li, Vakarelski and Thoroddsen2015).
3. Impact
The technological advances of high-speed video since the early 2000s have enabled experiments to access ever finer details of the droplet impact dynamics and they have been matched by progress in numerical techniques (García-Geijo, Riboux & Gordillo Reference García-Geijo, Riboux and Gordillo2024), thus breathing new life into this area of research (Josserand & Thoroddsen Reference Josserand and Thoroddsen2016). The significance of recent achievements is showcased by the number of relevant reviews, whose extensive reference lists convey the scale of the research effort. Moreover, there is a seemingly endless propensity for complex fluid phenomena when instead of simple fluids, fluid mixtures are used, possibly containing surfactants, polymers, salts and colloidal particles, or with external forcing, e.g. electrostatics, heat transfer, etc. Quantitative approaches combining controlled experiments and resolved numerical models can increasingly unravel their fluid dynamics, thus bridging the gap to applications in chemical engineering and colloid and interface science (Lohse & Zhang Reference Lohse and Zhang2020).
More specifically, the paper by Li et al. (Reference Li, Vakarelski and Thoroddsen2015) has been followed by a body of research characterising air entrainment in droplet impact under varied experimental conditions, including more complex roughness. Further investigation of impact on viscous-liquid substrates has confirmed enhanced-thickness air cushioning which masks the solid's roughness (Zhang et al. Reference Zhang, Soori, Rokoni, Kaminski and Sun2021). This can encourage skating by suppressing first contact. Maybe most notable is the double contact which occurs on freshly cleaved mica under reduced pressure conditions, entrapping an outer toroidal strip of air, which contracts into a ring of bubbles (Li et al. Reference Li, Langley, Tian, Hicks and Thoroddsen2017). Most recently, stunning visualisations with Fizeau interferometry by J. M. Kolinski (private communication 2024) have revealed that water–glycerol drops carrying sufficient charge can make point contact with freshly cleaved mica surfaces without measurable air entrapment (figure 2a), at impact velocities for which the drop traps air before rebounding when the charge is negligible (figure 2b).
Figure 2. Impact of a droplet of water ( ${\rm radius} = 1.03\ {\rm mm}$) on freshly cleaved mica, imaged with Fizeau interferometry at 60 kfps and 10 microsecond exposure time with a Photron Nova S16 camera. The impact velocity is
${\rm radius} = 1.03\ {\rm mm}$) on freshly cleaved mica, imaged with Fizeau interferometry at 60 kfps and 10 microsecond exposure time with a Photron Nova S16 camera. The impact velocity is  $V = 0.36\ {\rm m}\ {\rm s}^{-1}$. (a) For a droplet carrying a charge of 53 pC, no visible dimple region or air film appears; instead, contact occurs on the impact axis very rapidly, and the liquid spreads over the surface from first point of contact. (b) For a very small charge of 90 fC, the droplet fully rebounds during outward spreading. The rings in the centre of the impact region correspond to a dimple of trapped air. The dimple of trapped air is surrounded by a thinner, large-aspect-ratio air film (J. M. Kolinski, private communication 2024).
$V = 0.36\ {\rm m}\ {\rm s}^{-1}$. (a) For a droplet carrying a charge of 53 pC, no visible dimple region or air film appears; instead, contact occurs on the impact axis very rapidly, and the liquid spreads over the surface from first point of contact. (b) For a very small charge of 90 fC, the droplet fully rebounds during outward spreading. The rings in the centre of the impact region correspond to a dimple of trapped air. The dimple of trapped air is surrounded by a thinner, large-aspect-ratio air film (J. M. Kolinski, private communication 2024).
This wealth of experimental discovery and quantification has arguably placed experimental progress ahead of its theoretical counterpart. The various relevant effects involving the gas have been identified, namely compressibility, inertia, contact-line dynamics and non-continuum effects such as gas kinetic effects (GKE). While numerical models continue to test the relative importance of these effects, it is now fairly well accepted that GKE matter and allow us to reconcile different gas and ambient pressures during early impact (Sprittles Reference Sprittles2024). With continued technological advances and the pace of interdisciplinary research efforts, we can look forward to many more surprising droplet reveals on the nanoscale.
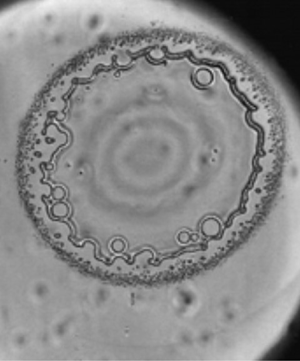

 ${\rm r.m.s.} = 7.3$ (glass) nm; (b)
${\rm r.m.s.} = 7.3$ (glass) nm; (b)  ${\rm r.m.s.} = 1.2$ nm (glass); (c)
${\rm r.m.s.} = 1.2$ nm (glass); (c)  ${\rm r.m.s.} < 0.5$ nm (freshly cleaved mica). The black arrow in each frame indicates the position of the outer boundary to the narrow fully wetted growing contact region. The white arrows point at microbubbles in (a,b) and the inner wetted edge in (c) where no micro-bubbles are entrapped. The scale bars are
${\rm r.m.s.} < 0.5$ nm (freshly cleaved mica). The black arrow in each frame indicates the position of the outer boundary to the narrow fully wetted growing contact region. The white arrows point at microbubbles in (a,b) and the inner wetted edge in (c) where no micro-bubbles are entrapped. The scale bars are  $100\ \mathrm {\mu }{\rm m}$ in (b) and
$100\ \mathrm {\mu }{\rm m}$ in (b) and  $50\ \mathrm {\mu }{\rm m}$ in (d). Adapted from Li et al. (2015).
$50\ \mathrm {\mu }{\rm m}$ in (d). Adapted from Li et al. (2015).
 ${\rm radius} = 1.03\ {\rm mm}$) on freshly cleaved mica, imaged with Fizeau interferometry at 60 kfps and 10 microsecond exposure time with a Photron Nova S16 camera. The impact velocity is
${\rm radius} = 1.03\ {\rm mm}$) on freshly cleaved mica, imaged with Fizeau interferometry at 60 kfps and 10 microsecond exposure time with a Photron Nova S16 camera. The impact velocity is  $V = 0.36\ {\rm m}\ {\rm s}^{-1}$. (a) For a droplet carrying a charge of 53 pC, no visible dimple region or air film appears; instead, contact occurs on the impact axis very rapidly, and the liquid spreads over the surface from first point of contact. (b) For a very small charge of 90 fC, the droplet fully rebounds during outward spreading. The rings in the centre of the impact region correspond to a dimple of trapped air. The dimple of trapped air is surrounded by a thinner, large-aspect-ratio air film (J. M. Kolinski, private communication 2024).
$V = 0.36\ {\rm m}\ {\rm s}^{-1}$. (a) For a droplet carrying a charge of 53 pC, no visible dimple region or air film appears; instead, contact occurs on the impact axis very rapidly, and the liquid spreads over the surface from first point of contact. (b) For a very small charge of 90 fC, the droplet fully rebounds during outward spreading. The rings in the centre of the impact region correspond to a dimple of trapped air. The dimple of trapped air is surrounded by a thinner, large-aspect-ratio air film (J. M. Kolinski, private communication 2024).
1. Introduction
The nanoscale pervades a remarkably vast array of fluid flows in nature and industry, encompassing the physicochemical hydrodynamics of biological systems, energy storage, chemical processing, nanotechnology, etc. (Lohse & Zhang Reference Lohse and Zhang2020). The everyday example of drop impact on a solid surface, e.g. the wetting of leaves by raindrops or the jetting of an inkjet printer nozzle, is inherently multiscale even for a ‘simple’ liquid like water, because nanoscale interactions influence the dynamics of the contact line which marks the boundary between liquid, gas and solid (Snoeijer & Andreotti Reference Snoeijer and Andreotti2013).
The rich and beautiful phenomenology of drop impact depends essentially on fluid dynamical parameters – Reynolds and Weber (We) numbers, which are ratios of inertial to viscous and inertial to capillary forces, respectively, and the ratios of liquid–gas densities and viscosities – but also on substrate parameters that emerge from the nanoscale (e.g. wettability, slip length, roughness distribution, etc.) The excellent recent reviews by Josserand & Thoroddsen (Reference Josserand and Thoroddsen2016) and Sprittles (Reference Sprittles2024) discuss the experimental and theoretical state-of-the-art in droplet impact, including the first contact with the substrate during early impact to which Li, Vakarelski & Thoroddsen (Reference Li, Vakarelski and Thoroddsen2015) make pioneering contributions.
Rapid advances in micro- and nano-technology in the past couple of decades have achieved scale reductions which have come to challenge the classical continuum framework of fluid dynamics and led to the emergence of the field of nanofluidics (Bocquet & Charlaix Reference Bocquet and Charlaix2010). It is now well accepted that the continuum framework holds up surprisingly well for bulk flows of simple fluids, with no apparent deviation from the bulk Navier–Stokes equations for confinements <10 nm for liquids, although mean free path estimates indicate that this limit is much increased for gases to $\sim$100 nm.
$\sim$100 nm.
The quest for the nanoscale has also equipped fluid dynamics with a phenomenal new toolset to resolve the smallest scales in time and space. In addition to ultra-fast direct imaging, examples include the surface force apparatus, which can measure disjoining pressures and their influence on thin film stability and contact-line motion, atomic force microscopy (AFM) for characterisation of substrates, as well as X-ray imaging, high-speed interferometry and total internal reflection which can capture nanoscale-thickness film dynamics.
So how do Li et al. (Reference Li, Vakarelski and Thoroddsen2015) probe the nanoscale in the context of droplet impact? By resolving the impact of a droplet on the hundreds of nanosecond scale to pinpoint the first contact, they are able to explore the role of prescribed nanometre-scale roughness by observing its effect on microscale contact-line dynamics. Hence, more than a century after the beauty and intricacy of splashing during droplet impact on a solid surface was first glimpsed by Worthington (Reference Worthington1876), Li et al. (Reference Li, Vakarelski and Thoroddsen2015) are able to combine 200 ns interframe times with spatial resolution down to the diffraction limit, thanks to the phenomenal advances in imaging technology of the last three decades. Their study was motivated by the recent discovery of the influence of the dynamics of thin gas films on the behaviour of liquid droplets (Xu, Zhang & Nagel Reference Xu, Zhang and Nagel2005). Immediately prior to impact, the lubrication pressure in the gas layer under the drop deforms the underside of the drop into a dimple, so that the first contact occurs along a circle, entrapping a thin gas bubble, which then rapidly contracts to minimise the surface energy. Complementary techniques, including total internal reflection (Kolinski, Mahadevan & Rubinstein Reference Kolinski, Mahadevan and Rubinstein2014) and interferometry (van der Veen et al. Reference van der Veen, Tran, Lohse and Sun2012; de Ruiter et al. Reference de Ruiter, Lagraaw, van den Ende and Mugele2015) have been able to resolve the film trapped between impacting surfaces to broadly reveal two modes of contact on a solid substrate, random contacts through a thin film, associated with prolonged skating for low $We$, and the outer kink mode for more rapid touchdown at higher We (Sprittles Reference Sprittles2024). The astounding images by Li et al. (Reference Li, Vakarelski and Thoroddsen2015) are a fitting illustration of the hive of activity on droplet impact in the 2010s but also a visual reminder that, however well resolved, yet unexplored nanoscale frontiers remain hidden within these images (see figure 1).
$We$, and the outer kink mode for more rapid touchdown at higher We (Sprittles Reference Sprittles2024). The astounding images by Li et al. (Reference Li, Vakarelski and Thoroddsen2015) are a fitting illustration of the hive of activity on droplet impact in the 2010s but also a visual reminder that, however well resolved, yet unexplored nanoscale frontiers remain hidden within these images (see figure 1).
Figure 1. (a–c) Close-up of the contracting contact line of the trapped air bubble 400 ns after impact of a millimetric water drop on substrates of decreasing root-mean-square (r.m.s.) measure of roughness: (a) ${\rm r.m.s.} = 7.3$ (glass) nm; (b)
${\rm r.m.s.} = 7.3$ (glass) nm; (b)  ${\rm r.m.s.} = 1.2$ nm (glass); (c)
${\rm r.m.s.} = 1.2$ nm (glass); (c)  ${\rm r.m.s.} < 0.5$ nm (freshly cleaved mica). The black arrow in each frame indicates the position of the outer boundary to the narrow fully wetted growing contact region. The white arrows point at microbubbles in (a,b) and the inner wetted edge in (c) where no micro-bubbles are entrapped. The scale bars are
${\rm r.m.s.} < 0.5$ nm (freshly cleaved mica). The black arrow in each frame indicates the position of the outer boundary to the narrow fully wetted growing contact region. The white arrows point at microbubbles in (a,b) and the inner wetted edge in (c) where no micro-bubbles are entrapped. The scale bars are  $100\ \mathrm {\mu }{\rm m}$ in (b) and
$100\ \mathrm {\mu }{\rm m}$ in (b) and  $50\ \mathrm {\mu }{\rm m}$ in (d). Adapted from Li et al. (Reference Li, Vakarelski and Thoroddsen2015).
$50\ \mathrm {\mu }{\rm m}$ in (d). Adapted from Li et al. (Reference Li, Vakarelski and Thoroddsen2015).
2. The art of ultra-fast imaging
Entrainment of air can be a limiting factor in industrial applications such as coating and printing, where bubbles degrade the quality and uniformity of the deposited film (Marchand et al. Reference Marchand, Chan, Snoeijer and Andreotti2012). The maximum radius of the entrapped air film during the early contact of an impacting droplet is set by the first contact, and it can be reliably predicted by balancing viscous lubrication in the thin air layer and the rapid deceleration of the drop inertia (Mandre, Mani & Brenner Reference Mandre, Mani and Brenner2009). In fact, the interplay of dynamic wetting and gas films in drop impact routinely leads to entrapment of a small bubble under its centre after retraction of the contact line, but Li et al. (Reference Li, Vakarelski and Thoroddsen2015) also identify the formation of a ring of microbubbles at first contact, due to multiple roughness-induced initial contacts just before the formation of the fully wetted outer section.
Experiments consisted of impacting millimetric water droplets onto three hydrophilic solid substrates, with AFM r.m.s. measures of roughness ranging from 7.3 nm and 1.2 nm for glass to <0.5 nm for freshly cleaved mica. The results are summarised in figure 1. On both types of glass slides (figure 1a,b), microbubbles are left behind at the site of first contact (black arrows) as the newly formed irregular bubbly contact line rapidly contracts into a central bubble. However, the reduction in substrate roughness to 1.2 nm drastically reduces the number of initial contacts so that the volume of air left behind and the irregularity of the contact line are much reduced. The bubbles are now so small that they are difficult to make out individually and the faint trace they leave in the vicinity of the contact line is only visible under suitable magnification and thus, not visible in figure 1(b). This reduction is consistent with the picture that nanobubbles owe their remarkable longevity to pinning of the three-phase contact line at chemical or geometric surface heterogeneities (Lohse & Zhang Reference Lohse and Zhang2015). Now with the mica (figure 1c), the images cannot capture any trace of micro/nanobubbles. Clearly, the molecular smoothness of the cleaved surface suppresses nanobubble formation, possibly compounded by perfect hydrophilicity compared with the small $20^\circ$ contact angle recorded with cleaned glass. This carries the interesting implication that a mechanism other than roughness acts to rupture the lubricating air film on which the drop initially skates, which Li et al. (Reference Li, Vakarelski and Thoroddsen2015) hypothesise to be van der Waals forces.
$20^\circ$ contact angle recorded with cleaned glass. This carries the interesting implication that a mechanism other than roughness acts to rupture the lubricating air film on which the drop initially skates, which Li et al. (Reference Li, Vakarelski and Thoroddsen2015) hypothesise to be van der Waals forces.
In an effort to investigate a perfectly smooth substrate, Li et al. (Reference Li, Vakarelski and Thoroddsen2015) switch to a millimetric layer of ultra-viscous silicone oil but this radically alters the early contact dynamics. The compliance of the substrate reduces the compression of the gas, enabling more air to be entrapped. Remarkably, microbubbles are again left behind the moving contact line, albeit not from localised contacts due to roughness. Instead, they are formed through the tip streaming of an azimuthal instability of the rapidly moving contact line. The instability wavelength increases linearly with film thickness, thus coarsening the contact-line deformation and increasing the size of the bubbles shed as the gas bubble contracts. Further experimental exploration by Pack et al. (Reference Pack, Kaneelil, Kim and Sun2018) using a high-speed total internal reflection microscopy technique has revealed that this instability is caused by the buildup of the gas pressure near the contact line which can lead to the entrainment of an air rim at the wetting front. Similar ideas may also apply to the small contact-line undulations observed on the low roughness solid substrates (see figure 1b,c), which were broadly assigned to the contact-line dynamics by Li et al. (Reference Li, Vakarelski and Thoroddsen2015).
3. Impact
The technological advances of high-speed video since the early 2000s have enabled experiments to access ever finer details of the droplet impact dynamics and they have been matched by progress in numerical techniques (García-Geijo, Riboux & Gordillo Reference García-Geijo, Riboux and Gordillo2024), thus breathing new life into this area of research (Josserand & Thoroddsen Reference Josserand and Thoroddsen2016). The significance of recent achievements is showcased by the number of relevant reviews, whose extensive reference lists convey the scale of the research effort. Moreover, there is a seemingly endless propensity for complex fluid phenomena when instead of simple fluids, fluid mixtures are used, possibly containing surfactants, polymers, salts and colloidal particles, or with external forcing, e.g. electrostatics, heat transfer, etc. Quantitative approaches combining controlled experiments and resolved numerical models can increasingly unravel their fluid dynamics, thus bridging the gap to applications in chemical engineering and colloid and interface science (Lohse & Zhang Reference Lohse and Zhang2020).
More specifically, the paper by Li et al. (Reference Li, Vakarelski and Thoroddsen2015) has been followed by a body of research characterising air entrainment in droplet impact under varied experimental conditions, including more complex roughness. Further investigation of impact on viscous-liquid substrates has confirmed enhanced-thickness air cushioning which masks the solid's roughness (Zhang et al. Reference Zhang, Soori, Rokoni, Kaminski and Sun2021). This can encourage skating by suppressing first contact. Maybe most notable is the double contact which occurs on freshly cleaved mica under reduced pressure conditions, entrapping an outer toroidal strip of air, which contracts into a ring of bubbles (Li et al. Reference Li, Langley, Tian, Hicks and Thoroddsen2017). Most recently, stunning visualisations with Fizeau interferometry by J. M. Kolinski (private communication 2024) have revealed that water–glycerol drops carrying sufficient charge can make point contact with freshly cleaved mica surfaces without measurable air entrapment (figure 2a), at impact velocities for which the drop traps air before rebounding when the charge is negligible (figure 2b).
Figure 2. Impact of a droplet of water ( ${\rm radius} = 1.03\ {\rm mm}$) on freshly cleaved mica, imaged with Fizeau interferometry at 60 kfps and 10 microsecond exposure time with a Photron Nova S16 camera. The impact velocity is
${\rm radius} = 1.03\ {\rm mm}$) on freshly cleaved mica, imaged with Fizeau interferometry at 60 kfps and 10 microsecond exposure time with a Photron Nova S16 camera. The impact velocity is  $V = 0.36\ {\rm m}\ {\rm s}^{-1}$. (a) For a droplet carrying a charge of 53 pC, no visible dimple region or air film appears; instead, contact occurs on the impact axis very rapidly, and the liquid spreads over the surface from first point of contact. (b) For a very small charge of 90 fC, the droplet fully rebounds during outward spreading. The rings in the centre of the impact region correspond to a dimple of trapped air. The dimple of trapped air is surrounded by a thinner, large-aspect-ratio air film (J. M. Kolinski, private communication 2024).
$V = 0.36\ {\rm m}\ {\rm s}^{-1}$. (a) For a droplet carrying a charge of 53 pC, no visible dimple region or air film appears; instead, contact occurs on the impact axis very rapidly, and the liquid spreads over the surface from first point of contact. (b) For a very small charge of 90 fC, the droplet fully rebounds during outward spreading. The rings in the centre of the impact region correspond to a dimple of trapped air. The dimple of trapped air is surrounded by a thinner, large-aspect-ratio air film (J. M. Kolinski, private communication 2024).
This wealth of experimental discovery and quantification has arguably placed experimental progress ahead of its theoretical counterpart. The various relevant effects involving the gas have been identified, namely compressibility, inertia, contact-line dynamics and non-continuum effects such as gas kinetic effects (GKE). While numerical models continue to test the relative importance of these effects, it is now fairly well accepted that GKE matter and allow us to reconcile different gas and ambient pressures during early impact (Sprittles Reference Sprittles2024). With continued technological advances and the pace of interdisciplinary research efforts, we can look forward to many more surprising droplet reveals on the nanoscale.
Acknowledgements
The author thanks D. Pihler-Puzović, J. E. Sprittles, S. T. Thoroddsen, D. Lohse and J. A. Neufeld for helpful comments on this manuscript and J. M. Kolinski for sharing images of recent experiments he presented at ICTAM 2024 in Daegu, South Korea.
Declaration of interests
The author reports no conflict of interest.