Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T05:18:42.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional unsteadiness map of oblique shock wave/boundary layer interaction with sidewalls

Published online by Cambridge University Press:  24 May 2019

P. K. Rabey Open the ORCID record for P. K. Rabey [Opens in a new window] ,
S. P. Jammy ,
P. J. K. Bruce Open the ORCID record for P. J. K. Bruce [Opens in a new window]  and
N. D. Sandham Open the ORCID record for N. D. Sandham [Opens in a new window]
P. K. Rabey*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
S. P. Jammy
Affiliation:
Department of Mechanical Engineering, School of Engineering and Applied Sciences, SRM University AP Amaravati, India
P. J. K. Bruce
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
N. D. Sandham
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The low-frequency unsteadiness of oblique shock wave/boundary layer interactions (SBLIs) has been investigated using large-eddy simulation (LES) and high-frequency pressure measurements from experiments. Particular attention has been paid to off-centreline behaviour: the LES dataset was generated including sidewalls, and experimental pressure measurements were acquired across the entire span of the reflected shock foot. The datasets constitute the first maps of low-frequency unsteadiness in both streamwise and spanwise directions. The results reveal that significant low-frequency shock motion (with 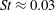$St\approx 0.03$) occurs away from the centreline, along most of the central separation shock and in the corner regions. The most powerful low-frequency unsteadiness occurs off-centre, likely due to the separation shock being strengthened by shocks arising from the swept interactions on the sidewalls. Both simulation and experimental results exhibit asymmetry about the spanwise centre. In simulations, this may be attributed to a lack of statistical convergence; however, the fact that this is also seen in experiments is indicative that some SBLIs may exhibit some inherent asymmetry across the two spanwise halves of the separation bubble. There is also significant low-frequency power in the corner separations. The relation of the unsteadiness in the corner regions to that in the centre is investigated by means of two-point correlations: a key observation is that significant correlation does not extend across the attached flow channel between the central and corner separations.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , R4
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babinsky, H. & Harvey, J. K. 2011 Shock Wave–Boundary-Layer Interactions. Cambridge University Press.Google Scholar
Babinsky, H., Oorebeek, J. & Cottingham, T. G. 2013 Corner effects in reflecting oblique shock-wave/boundary-layer interactions. In 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, pp. 1–10. AIAA.Google Scholar
Benek, J. A., Suchyta, C. J. & Babinsky, H. 2014 The effect of wind tunnel size and shock strength on incident shock boundary layer interaction experiments. In AIAA Aviation Forum (June), pp. 1–30. AIAA.Google Scholar
Benek, J. A., Suchyta, C. J. & Babinsky, H. 2016 Simulations of incident shock boundary layer interactions. In 54th AIAA Aerospace Sciences Meeting, pp. 1–26. AIAA.Google Scholar
Bruce, P. J. K., Burton, D. M. F., Titchener, N. A. & Babinsky, H. 2011 Corner effect and separation in transonic channel flows. J. Fluid Mech. 679, 247–262.10.1017/jfm.2011.135Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46 (September), 469–492.10.1146/annurev-fluid-010313-141346Google Scholar
Dupont, P., Haddad, C., Ardissone, J. P. & Debiève, J.-F. 2005 Space and time organisation of a shock wave/turbulent boundary layer interaction. Aerosp. Sci. Technol. 9 (7), 561–572.10.1016/j.ast.2004.12.009Google Scholar
Dupont, P., Haddad, C. & Debiève, J.-F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.10.1017/S0022112006000267Google Scholar
Dussauge, J.-P., Dupont, P. & Debiève, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10, 85–91.10.1016/j.ast.2005.09.006Google Scholar
Funderburk, M. & Narayanaswamy, V. 2016 Experimental investigation of primary and corner shock boundary layer interactions at mild back pressure ratios. Phys. Fluids 28 (8), 086102.10.1063/1.4960963Google Scholar
Garnier, E. 2009 Stimulated detached eddy simulation of three-dimensional shock/boundary layer interaction. Shock Waves 19 (6), 479–486.Google Scholar
Grossman, I. J. & Bruce, P. J. K. 2018 Confinement effects on regular–irregular transition in shock-wave–boundary-layer interactions. J. Fluid Mech. 853, 171–204.10.1017/jfm.2018.537Google Scholar
Pasquariello, V., Hickel, S. & Adams, N. A. 2017 Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number. J. Fluid Mech. 823, 617–657.10.1017/jfm.2017.308Google Scholar
Poggie, J. & Porter, K. M. 2018 Numerical simulation of sidewall influence on supersonic compression ramp interactions. In 2018 Fluid Dynamics Conference, pp. 1–9. AIAA.Google Scholar
Wang, B., Sandham, N. D., Hu, Z. & Liu, W. 2015 Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects. J. Fluid Mech. 767, 526–561.Google Scholar