Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T05:09:58.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional numerical study of vortex shedding regimes of oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds numbers

Published online by Cambridge University Press:  16 June 2014

Ming Zhao  and
Liang Cheng
Ming Zhao*
Affiliation:
School of Computing, Engineering and Mathematics, University of Western Sydney, Locked Bag 1797, Penrith, NSW 2751, Australia
Liang Cheng
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds numbers is simulated numerically by solving the two-dimensional Navier–Stokes (NS) equations using a finite-element method (FEM). The aim of this study is to identify the flow regimes of the two-cylinder system at different gap arrangements and Keulegan–Carpenter numbers (KC). Simulations are conducted at seven gap ratios 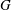$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ (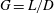$G=L/D$ where 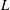$L$ is the cylinder-to-cylinder gap and 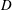$D$ the diameter of a cylinder) of 0.5, 1, 1.5, 2, 3, 4 and 5 and KC ranging from 1 to 12 with an interval of 0.25. The flow regimes that have been identified for oscillatory flow around a single cylinder are also observed in the two-cylinder system but with different flow patterns due to the interactions between the two cylinders. In the side-by-side arrangement, the vortex shedding from the gap between the two cylinders dominates when the gap ratio is small, resulting in the gap vortex shedding (GVS) regime, which is different from any of the flow regimes identified for a single cylinder. For intermediate gap ratios of 1.5 and 2 in the side-by-side arrangement, the vortex shedding mode from one side of each cylinder is not necessarily the same as that from the other side, forming a so-called combined flow regime. When the gap ratio between the two cylinders is sufficiently large, the vortex shedding from each cylinder is similar to that of a single cylinder. In the tandem arrangement, when the gap between the two cylinders is very small, the flow regimes are similar to that of a single cylinder. For large gap ratios in the tandem arrangement, the vortex shedding flows from the gap side of the two cylinders interact and those from the outer sides of the cylinders are less affected by the existence of the other cylinder and similar to that of a single cylinder. Strong interaction between the vortex shedding flows from the two cylinders makes the flow very irregular at large KC values for both side-by-side and tandem arrangements.

JFM classification

Mathematical Foundations: Computational methods Low-Reynolds-number flows: Low-Reynolds-number flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 1 - 37
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. M., Moriya, M. & Sakamoto, H. 2003 Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. J. Fluids Struct. 18, 325–346.Google Scholar
An, H., Cheng, L. & Zhao, M. 2009 Steady streaming around a circular cylinder in an oscillatory flow. Ocean Engng 36, 1089–1097.Google Scholar
An, H., Cheng, L. & Zhao, M. 2011 Direct numerical simulation of oscillatory flow around a circular cylinder at low Keulegan–Carpenter number. J. Fluid Mech. 666, 77–103.Google Scholar
Anagnostopoulos, P. & Minear, R. 2004 Blockage effect of oscillatory flow past a fixed cylinder. Appl. Ocean Res. 26, 147–153.Google Scholar
Bao, Y., Zhou, D. & Tu, J. 2011 Flow interference between a stationary cylinder and an elastically mounted cylinder arranged in proximity. J. Fluids Struct. 27, 1425–1446.CrossRefGoogle Scholar
Bearman, P. W., Downie, M. J., Graham, J. M. R. & Obasaju, E. D. 1985 Forces on cylinders in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 154, 337–356.Google Scholar
Bearman, P. W., Graham, J. M. R., Naylor, P. & Obasaju, D. E.1981 The role of vortices in oscillatory flow about bluff cylinders International Symposium on Hydrodynamics in Ocean Engineering, Norwegian Hydrodynamics Laboratories, Trondheim, pp. 621–635.Google Scholar
Bearman, P. W. & Wadcock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61, 499–511.Google Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region. J. Fluid Mech. 621, 321–364.CrossRefGoogle ScholarPubMed
Brooks, A. N. & Hughes, T. J. R. 1982 Streamline upwind/Petrov–Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput. Meth. Appl. Mech. Engng 32, 199–259.Google Scholar
Chern, M. J., Kanna, P. R., Lu, Y. J., Cheng, I. C. & Chang, S. C. 2010 A CFD study of the interaction of oscillatory flows with a pair of side-by-side cylinders. J. Fluids Struct. 26, 626–643.Google Scholar
Coenen, W. & Riley, N. 2009 Oscillatory flow about a cylinder pair. Q. J. Mech. Appl. Maths 62 (1), 53–66.CrossRefGoogle Scholar
Dütsch, H., Durst, F. & Becker, S. 1998 Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers. J. Fluid Mech. 360, 249–271.Google Scholar
Elston, J. R., Blackburn, H. M. & Sheridan, J. 2006 The primary and secondary instabilities of flow generated by an oscillating circular cylinder. J. Fluid Mech. 550, 359–389.Google Scholar
Elston, J. R., Sheridan, J. & Blackburn, H. M. 2004 Two-dimensional Floquet stability analysis of the flow produced by an oscillating circular cylinder in quiescent fluid. Eur. J. Mech. (B/Fluids) 23, 99–106.Google Scholar
Hall, P. 1984 On the stability of the unsteady boundary layer on a cylinder oscillating transversely in a viscous fluid. J. Fluid Mech. 146, 347–367.Google Scholar
Honji, H. 1981 Streaked flow around an oscillating circular cylinder. J. Fluid Mech. 107, 507–520.CrossRefGoogle Scholar
Hover, F. S., Techet, A. H. & Triantafyllou, M. S. 1998 Forces on oscillating uniform and tapered cylinders in cross flow. J. Fluid Mech. 363, 97–114.CrossRefGoogle Scholar
Iliadis, G. & Anagnostopoulos, P. 1998 Numerical visualization of oscillatory flow around a circular cylinder at $\mathit{Re}=200$ and $\mathit{KC}=20$ – an aperiodic flow case. Commun. Numer. Meth. Engng 14, 181–194.Google Scholar
Jester, W. & Kallinderis, Y. 2004 Numerical study of incompressible flow about transversely oscillating cylinder pairs. J. Offshore Mech. Arctic Engng 126 (4), 310–317.Google Scholar
Justensen, P. 1991 A numerical study of oscillating flow around a circular cylinder. J. Fluid Mech. 222, 157–196.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Investigation of the flow between a pair of cylinders in the flopping regime. J. Fluid Mech. 196, 431–448.CrossRefGoogle Scholar
Kühtz, S.1996 Experimental investigation of oscillatory flow around circular cylinders at low beta numbers. PhD thesis, University of London.Google Scholar
Lin, X. W., Bearman, P. W. & Graham, J. M. R. 1996 A numerical study of oscillatory flow about a circular cylinder for low values of beta parameters. J. Fluids Struct. 10, 501–526.Google Scholar
Meneghini, J. R., Saltara, F., Siqueira, C. L. R. & Ferrari, J. J. A. 2001 Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15 (2), 327–350.Google Scholar
Mittal, S. & Kumar, V. 2001 Flow-induced oscillations of two cylinders in tandem and staggered arrangements. J. Fluids Struct. 15 (5), 717–736.Google Scholar
Mittal, S. & Kumar, V. 2004 Vortex induced vibrations of a pair of cylinders at Reynolds number 1000. Intl J. Comput. Fluid Dyn. 18, 601–614.Google Scholar
Mizushima, J. & Suehiro, N. 2005 Instability and transition of flow past two tandem circular cylinders. Phys. Fluids 17 (10), 104107.CrossRefGoogle Scholar
Morison, J. R., O’Brien, M. P., Johnson, J. W. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2 (5), 149–154.Google Scholar
Morse, T. L., Govardhan, R. N. & Williamson, C. H. K. 2008 The effect of end conditions on the vortex-induced vibration of cylinders. J. Fluids Struct. 24, 1227–1239.Google Scholar
Nehari, D., Armenio, V. & Ballio, F. 2004 Three-dimensional analysis of the unidirectional oscillatory flow around a circular cylinder at low Keulegan–Carpenter and $\beta $ numbers. J. Fluid Mech. 520, 157–186.CrossRefGoogle Scholar
Nemes, A., Zhao, J., Jacono, D. L. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.CrossRefGoogle Scholar
Obasaju, E. D., Bearman, P. W. & Graham, J. M. R. 1988 A study of forces, circulation and vortex patterns around a circular cylinder in oscillating flow. J. Fluid Mech. 196, 467–494.Google Scholar
Sarpkaya, T. 1986 Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 165, 61–71.Google Scholar
Sarpkaya, T. 2002 Experiments on the stability of sinusoidal flow over a circular cylinder. J. Fluid Mech. 457, 157–180.Google Scholar
Sarpkaya, T. 2005 On the parameter $\beta =\mathit{Re}/\mathit{KC} =D^{2}/\nu T$ . J. Fluids Struct. 21, 435–440.Google Scholar
Sarpkaya, T. 2006 Structures of separation on a circular cylinder in periodic flow. J. Fluid Mech. 567, 281–297.Google Scholar
Scandura, P., Armenio, V. & Foti, E. 2009 Numerical investigation of the oscillatory flow around a circular cylinder close to a wall at moderate Keulegan–Carpenter and low Reynolds numbers. J. Fluid Mech. 627, 259–290.Google Scholar
Tasaka, Y., Kon, S., Schouveiler, L. & Gal, P. L. 2006 Hysteretic mode exchange in the wake of two circular cylinders in tandem. Phys. Fluids 18, 084101.Google Scholar
Tatsuno, M. & Bearman, P. W. 1990 A visual study of the flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers and low Stokes numbers. J. Fluid Mech. 211, 157–182.Google Scholar
Uzunoglu, B., Tan, M. & Price, W. G. 2001 Low-Reynolds-number flow around an oscillating circular cylinder using a cell viscous boundary element method. Intl J. Numer. Meth. Engng 50, 2317–2338.CrossRefGoogle Scholar
Williamson, C. H. K. 1985a Sinusoidal flow relative to circular cylinders. J. Fluid Mech. 155, 141–174.CrossRefGoogle Scholar
Williamson, C. H. K. 1985b Evolution of a single wake behind a pair of bluff bodies. J. Fluid Mech. 159, 1–18.CrossRefGoogle Scholar
Yang, K., Cheng, L., An, H., Bassom, A. P. & Zhao, M. 2013 The effect of a piggyback cylinder on the flow characteristics in oscillatory flow. Ocean Engng 62, 45–55.CrossRefGoogle Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.Google Scholar
Zdravkovich, M. M. 1988 Review of interference-induced oscillations in flow past two parallel circular cylinders in various arrangements. J. Wind Engng Ind. Aerodyn. 28, 183–200.Google Scholar
Zdravkovich, M. M. & Pridden, D. L. 1977 Interference between two circular cylinders, series of unexpected discontinuities. J. Ind. Aerodyn. 2, 255–270.Google Scholar
Zhao, M. 2013 Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150. Phys. Fluids 25, 123601.Google Scholar
Zhao, M., Cheng, L., Teng, B. & Dong, G. 2007 Hydrodynamic forces on dual cylinders of different diameters in steady flow. J. Fluids Struct. 23, 59–83.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2009 Numerical simulation of three-dimensional flow past a yawed circular cylinder. J. Fluids Struct. 25, 831–847.Google Scholar
Zhao, M., Thapa, J., Cheng, L. & Zhou, T. 2013 Three-dimensional transition of vortex-shedding flow around a circular cylinder at right and oblique attacks. Phys. Fluids 25, 014105.Google Scholar