Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T05:18:30.667Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional cross-spectrum of the streamwise velocity in turbulent boundary layers

Published online by Cambridge University Press:  02 March 2020

Rahul Deshpande Open the ORCID record for Rahul Deshpande [Opens in a new window] ,
Dileep Chandran Open the ORCID record for Dileep Chandran [Opens in a new window] ,
Jason P. Monty Open the ORCID record for Jason P. Monty [Opens in a new window]  and
Ivan Marusic Open the ORCID record for Ivan Marusic [Opens in a new window]
Rahul Deshpande*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC3010, Australia
Dileep Chandran
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC3010, Australia
Jason P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we present the two-dimensional (2-D) energy cross-spectrum of the streamwise velocity ($u$) component and use it to test the notion of self-similarity in turbulent boundary layers. The primary focus is on the cross-spectrum ($\unicode[STIX]{x1D6F7}_{cross}^{w}$) measured across the logarithmic ($z_{o}$) and near-wall ($z_{r}$) wall-normal locations, providing the energy distribution across the range of streamwise ($\unicode[STIX]{x1D706}_{x}$) and spanwise ($\unicode[STIX]{x1D706}_{y}$) wavelengths (or length scales) that are coherent across the wall-normal distance. $\unicode[STIX]{x1D6F7}_{cross}^{w}$ may thus be interpreted as a wall-filtered subset of the full 2-D $u$-spectrum ($\unicode[STIX]{x1D6F7}$), the latter providing information on all coexisting eddies at $z_{o}$. To this end, datasets comprising synchronized two-point $u$-signals at $z_{o}$ and $z_{r}$, across the friction Reynolds number range $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3}){-}O(10^{4})$, are analysed. The published direct numerical simulation (DNS) dataset of Sillero et al. (Phys. Fluids, vol. 26 (10), 2014, 105109) is considered for low-$Re_{\unicode[STIX]{x1D70F}}$ analysis, while the high-$Re_{\unicode[STIX]{x1D70F}}$ dataset is obtained by conducting synchronous multipoint hot-wire measurements. 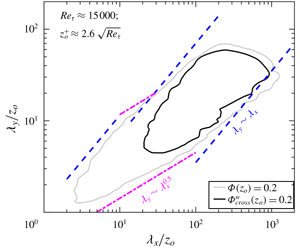High-$Re_{\unicode[STIX]{x1D70F}}$ cross-spectra reveal that the wall-attached large scales follow a $\unicode[STIX]{x1D706}_{y}/z_{o}\sim \unicode[STIX]{x1D706}_{x}/z_{o}$ relationship more closely than seen for $\unicode[STIX]{x1D6F7}$, where this self-similar trend is obscured by coexisting scales. The present analysis reaffirms that a self-similar structure, conforming to Townsend’s attached eddy hypothesis, is ingrained in the flow.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , R2
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agostini, L. & Leschziner, M. 2017 Spectral analysis of near-wall turbulence in channel flow at Re 𝜏 = 4200 with emphasis on the attached-eddy hypothesis. Phys. Rev. Fluids 2 (1), 014603.CrossRefGoogle Scholar
del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.CrossRefGoogle Scholar
Baars, W. J. & Marusic, I. 2020 Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra. J. Fluid Mech. 882, A25.Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Chandran, D.2019 Characteristics of energetic motions in turbulent boundary layers. PhD thesis, University of Melbourne, Department of Mechanical Engineering.Google Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2016 Measurement of two-dimensional energy spectra in a turbulent boundary layer. In Proceedings of 20th Australasian Fluid Mechanics Conference.Google Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2017 Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 826, R1.CrossRefGoogle Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Davidson, P. A., Nickels, T. B. & Krogstad, P.-Å. 2006 The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.CrossRefGoogle Scholar
Deshpande, R., Monty, J. P. & Marusic, I. 2019 Streamwise inclination angle of large wall-attached structures in turbulent boundary layers. J. Fluid Mech. 877, R4.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hwang, J. & Sung, H. J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.CrossRefGoogle Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.CrossRefGoogle Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26 (10), 105109.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Yoon, M., Hwang, J., Yang, J. & Sung, H. J. 2020 Wall-attached structures of streamwise velocity fluctuations in an adverse-pressure-gradient turbulent boundary layer. J. Fluid Mech. 885, A12.CrossRefGoogle Scholar