Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-10T05:39:47.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Two tandem cylinders of different diameters in cross-flow: flow-induced vibration

Published online by Cambridge University Press:  22 September 2017

Bin Qin ,
Md. Mahbub Alam Open the ORCID record for Md. Mahbub Alam [Opens in a new window]  and
Yu Zhou
Bin Qin
Affiliation:
Institute for Turbulence–Noise–Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
Md. Mahbub Alam*
Affiliation:
Institute for Turbulence–Noise–Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
Yu Zhou
Affiliation:
Institute for Turbulence–Noise–Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

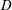This paper presents a systematic study of the cross-flow-induced vibration on a spring-supported circular cylinder of diameter $D$ placed in the wake of a fixed cylinder of smaller diameter 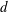$d$. The ratios $d/D$ and 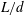$L/d$ are varied from 0.2 to 1.0 and from 1.0 to 5.5, respectively, where 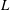$L$ is the distance between the centre of the upstream cylinder to the forward stagnation point of the downstream cylinder. Extensive measurements are conducted to capture the cylinder vibration and frequency responses, surface pressure, shedding frequencies and flow fields using laser vibrometer, hot-wire, pressure scanner and particle image velocimetry techniques. Six distinct flow regimes are identified. It has been found that a violent vibration may erupt for the spring-supported cylinder, and its dependence on 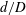$d/D$ and 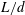$L/d$ is documented. A careful examination and analysis of the flow structure, along with the simultaneously captured pressure distribution around and vibration of the downstream cylinder, cast light upon the mechanisms behind this vibration and its sustainability. The roles of added mass, flow-induced damping and physical aspects in the process of initiating the vibration are discussed in detail.

JFM classification

Vortex Flows: Vortex interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 621 - 658
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. M. 2014 The aerodynamics of a cylinder submerged in the wake of another. J. Fluids Struct. 51, 393–400.CrossRefGoogle Scholar
Alam, M. M. 2016 Lift forces induced by the phase lag between the vortex sheddings from two tandem bluff bodies. J. Fluids Struct. 65, 217–237.CrossRefGoogle Scholar
Alam, M. M. & Meyer, J. P. 2013 Global aerodynamic instability of twin cylinders in cross flow. J. Fluids Struct. 41, 135–145.CrossRefGoogle Scholar
Alam, M. M., Moriya, M., Takai, K. & Sakamoto, H. 2003 Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number. J. Wind Engng Ind. Aerodyn. 91, 139–154.CrossRefGoogle Scholar
Alam, M. M. & Sakamoto, H. 2005 Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets. J. Fluids Struct. 20, 425–449.Google Scholar
Alam, M. M. & Zhou, Y. 2007 The turbulent wake of an inclined cylinder with water running. J. Fluid Mech. 589, 261–303.CrossRefGoogle Scholar
Alam, M. M. & Zhou, Y. 2008 Strouhal numbers, forces and flow structures around two tandem cylinders of different diameters. J. Fluids Struct. 24, 505–526.CrossRefGoogle Scholar
Arie, M., Kiya, M., Moriya, M. & Mori, H. 1983 Pressure fluctuations on the surface of two circular cylinders in tandem arrangement. Trans. ASME J. Fluids Engng 105 (2), 161–166.CrossRefGoogle Scholar
Assi, G. R. 2014 Wake-induced vibration of tandem cylinders of different diameters. J. Fluids Struct. 50, 329–339.CrossRefGoogle Scholar
Assi, G. R. S., Bearman, P. W., Carmo, B. S., Meneghini, J. R., Sherwin, S. J. & Willden, R. H. J. 2013 The role of wake stiffness on the wake-induced vibration of the downstream cylinder of a tandem pair. J. Fluid Mech. 718, 210–245.CrossRefGoogle Scholar
Assi, G. R. S., Bearman, P. W. & Meneghini, J. R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.CrossRefGoogle Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16 (1), 195–222.CrossRefGoogle Scholar
Bearman, P. W., Gartshore, I. S., Maull, D. J. & Parkinson, G. V. 1987 Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1 (1), 19–34.CrossRefGoogle Scholar
Bokaian, A. & Geoola, F. 1984a Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 383–415.CrossRefGoogle Scholar
Bokaian, A. & Geoola, F. 1984b Proximity-induced galloping of two interfering circular cylinders. J. Fluid Mech. 146, 417–449.CrossRefGoogle Scholar
Brika, D. & Laneville, A. 1997 Wake interference between two circular cylinders. J. Wind Engng Ind. Aerodyn. 72, 61–70.CrossRefGoogle Scholar
Brika, D. & Laneville, A. 1999 The flow interaction between a stationary cylinder and a downstream flexible cylinder. J. Fluids Struct. 13, 579–606.CrossRefGoogle Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010 Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing. Phys. Fluids 22 (5), 054101.CrossRefGoogle Scholar
Cooper, K. R. & Wardlaw, R. L. 1971 Aeroelastic instabilities in wakes. In Proc. 3rd Int. Conf. on Wind Effects on Buildings and Structures, pp. 647–655. Tokyo.Google Scholar
Dielen, B. & Ruscheweyh, H. 1995 Mechanism of interference galloping of two identical circular cylinders in cross flow. J. Wind Engng Ind. Aerodyn. 54, 289–300.CrossRefGoogle Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25 (02), 401–413.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Hori, E. I. 1959 Experiments on flow around a pair of parallel circular cylinders. In Proc. 9th Japan Nut. Cong. Appl. Mech., pp. 231–234. Tokyo.Google Scholar
Hover, F. S. & Triantafyllou, M. S. 2001 Galloping response of a cylinder with upstream wake interference. J. Fluids Struct. 15, 503–512.CrossRefGoogle Scholar
Huang, S. & Sworn, A. 2011 Some observations of two interfering VIV circular cylinders of unequal diameters in tandem. J. Hydrodyn. Ser. B 23 (5), 535–543.CrossRefGoogle Scholar
Huang, S. & Sworn, A. 2013 Interference between two stationary or elastically supported rigid circular cylinders of unequal diameters in tandem and staggered arrangements. J. Offshore Mech. Arctic Engng 135 (2), 021803.Google Scholar
Igarashi, T. 1981 Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bull. JSME 24 (188), 323–331.Google Scholar
Igarashi, T. 1982 Characteristics of a flow around two circular cylinders of different diameters arranged in tandem. Bull. JSME 25, 349–357.CrossRefGoogle Scholar
Igarashi, T. 1984 Characteristics of the flow around two circular cylinders arranged in tandem: 2nd report. Unique phenomenon at small spacing. Bull. JSME 27 (233), 2380–2387.CrossRefGoogle Scholar
Jeon, D. & Gharib, M. 2004 On the relationship between the vortex formation process and cylinder wake vortex patterns. J. Fluid Mech. 519, 161–181.CrossRefGoogle Scholar
Jester, W. & Kallinderis, Y. 2003 Numerical study of incompressible flow about fixed cylinder pairs. J. Fluids Struct. 17, 561–577.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. 1997 Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind Engng Ind. Aerodyn. 69, 341–350.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7–8), 813–851.CrossRefGoogle Scholar
Kim, S., Alam, M. M., Sakamoto, H. & Zhou, Y. 2009 Flow-induced vibrations of two circular cylinders in tandem arrangement. Part 1: Characteristics of vibration. J. Wind Engng Ind. Aerodyn. 97, 304–311.CrossRefGoogle Scholar
Knisely, C. W. & Kawagoe, M. 1990 Force–displacement measurements on closely spaced tandem cylinders. J. Wind Engng Ind. Aerodyn. 33 (1–2), 81–90.CrossRefGoogle Scholar
Lam, K. M. & To, A. P. 2003 Interference effect of an upstream larger cylinder on the lock-in vibration of a flexibly mounted circular cylinder. J. Fluids Struct. 17, 1059–1078.CrossRefGoogle Scholar
Laneville, A. & Brika, D. 1999 The fluid and mechanical coupling between two circular cylinders in tandem arrangement. J. Fluids Struct. 13, 967–986.CrossRefGoogle Scholar
Leontini, J. S., Stewart, B. E., Thompson, M. C. & Hourigan, K. 2006 Predicting vortex-induced vibration from driven oscillation results. Appl. Math. Model. 30 (10), 1096–1102.CrossRefGoogle Scholar
Lin, C. & Hsieh, S. C. 2003 Convection velocity of vortex structures in the near wake of a circular cylinder. J. Engng Mech. 129 (10), 1108–1118.Google Scholar
Lin, J. C., Yang, Y. & Rockwell, D. 2002 Flow past two cylinders in tandem: instantaneous and averaged flow structure. J. Fluids Struct. 16 (8), 1059–1071.CrossRefGoogle Scholar
Ljungkrona, L., Norberg, C. H. & Sunden, B. 1991 Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement. J. Fluids Struct. 5 (6), 701–727.Google Scholar
Mahir, N. & Rockwell, D. 1996 Vortex formation from a forced system of two cylinders. Part I: tandem arrangement. J. Fluids Struct. 10, 473–490.Google Scholar
Mittal, S. & Kumar, V. 2001 Flow-induced oscillations of two cylinders in tandem and staggered arrangements. J. Fluids Struct. 15 (5), 717–736.CrossRefGoogle Scholar
Morse, T. L. & Williamson, C. H. K. 2009a Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.CrossRefGoogle Scholar
Morse, T. L. & Williamson, C. H. K. 2009b Fluid forcing, wake modes, and transitions for a cylinder undergoing controlled oscillations. J. Fluids Struct. 25, 697–712.Google Scholar
Pan, Z. Y., Cui, W. C. & Miao, Q. M. 2007 Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code. J. Fluids Struct. 23 (1), 23–37.CrossRefGoogle Scholar
Prasanth, T. K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.CrossRefGoogle Scholar
Rahmanian, M., Zhao, M., Cheng, L. & Zhou, T. 2012 Two-degree-of-freedom vortex-induced vibration of two mechanically coupled cylinders of different diameters in steady current. J. Fluids Struct. 35, 133–159.CrossRefGoogle Scholar
Ruscheweyh, H. & Dielen, B. 1992 Interference galloping-investigations concerning the phase lag of the flow switching. J. Wind Engng Ind. Aerodyn. 43 (1–3), 2047–2056.CrossRefGoogle Scholar
Sen, S. & Mittal, S. 2015 Effect of mass ratio on free vibrations of a square cylinder at low Reynolds numbers. J. Fluids Struct. 54, 661–678.CrossRefGoogle Scholar
Sen, S. & Mittal, S. 2016 Free vibrations of a square cylinder of varying mass ratios. Procedia Engng 144, 34–42.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
Xu, G. & Zhou, Y. 2004 Strouhal numbers in the wake of two inline cylinders. Exp. Fluids 37, 248–256.CrossRefGoogle Scholar
Zdravkovich, M. M. 1974 Flow-induced vibration of two cylinders in tandem arrangements, and their suppression. In Proceedings of the International Symposium on Flow Induced Structural Vibrations, Karlsruhe 1972, pp. 631–639. Springer.Google Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.CrossRefGoogle Scholar
Zdravkovich, M. M. 1988 Review of interference-induced oscillations in flow past two parallel circular cylinders in various arrangements. J. Wind Engng Ind. Aerodyn. 28 (1–3), 183–199.Google Scholar
Zhao, M. & Yan, G. 2013 Numerical simulation of vortex-induced vibration of two circular cylinders of different diameters at low Reynolds number. Phys. Fluids 25 (8), 083601.Google Scholar
Zhou, Y. & Alam, M. M. 2016 Wake of two interacting circular cylinders: a review. Intl J. Heat Fluid Flow 62, 510–537.CrossRefGoogle Scholar
Zhou, Y., Feng, S. X., Alam, M. M. & Bai, H. L. 2009 Reynolds number effect on the wake of two staggered cylinders. Phys. Fluids 21, 125105.CrossRefGoogle Scholar
Zhou, Y. & Yiu, M. W. 2006 Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 548, 17–48.CrossRefGoogle Scholar