Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
McConnochie, Craig D.
and
Kerr, Ross C.
2016.
The effect of a salinity gradient on the dissolution of a vertical ice face.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
589.
Gayen, Bishakhdatta
Griffiths, Ross W.
and
Kerr, Ross C.
2016.
Simulation of convection at a vertical ice face dissolving into saline water.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
284.
McConnochie, C. D.
and
Kerr, R. C.
2017.
Testing a common ice‐ocean parameterization with laboratory experiments.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 7,
p.
5905.
FitzMaurice, A.
Cenedese, C.
and
Straneo, F.
2017.
Nonlinear response of iceberg side melting to ocean currents.
Geophysical Research Letters,
Vol. 44,
Issue. 11,
p.
5637.
McConnochie, Craig D.
and
Kerr, Ross C.
2017.
Enhanced ablation of a vertical ice wall due to an external freshwater plume.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
429.
Beckmann, Johanna
Perrette, Mahé
and
Ganopolski, Andrey
2018.
Simple models for the simulation of submarine melt for a Greenland glacial system model.
The Cryosphere,
Vol. 12,
Issue. 1,
p.
301.
Kaye, N. B.
and
Cooper, P.
2018.
Source and boundary condition effects on unconfined and confined vertically distributed turbulent plumes.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
1032.
Bonnebaigt, Rachael
Caulfield, C. P.
and
Linden, P. F.
2018.
Detrainment of plumes from vertically distributed sources.
Environmental Fluid Mechanics,
Vol. 18,
Issue. 1,
p.
3.
Nie, Bingchuan
and
Xu, Feng
2019.
Scales of natural convection on a convectively heated vertical wall.
Physics of Fluids,
Vol. 31,
Issue. 2,
Loganathan, R. M.
and
Hunt, G. R.
2019.
Analytical solutions for flow induced by a vertically distributed turbulent plume.
Environmental Fluid Mechanics,
Vol. 19,
Issue. 4,
p.
801.
Mondal, Mainak
Gayen, Bishakhdatta
Griffiths, Ross W.
and
Kerr, Ross C.
2019.
Ablation of sloping ice faces into polar seawater.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
545.
Hewitt, Ian J.
2020.
Subglacial Plumes.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
145.
Rosevear, Madelaine Gamble
Gayen, Bishakhdatta
and
Galton-Fenzi, Benjamin Keith
2021.
The role of double-diffusive convection in basal melting of Antarctic ice shelves.
Proceedings of the National Academy of Sciences,
Vol. 118,
Issue. 6,
Parker, D. A.
Burridge, H. C.
Partridge, J. L.
and
Linden, P. F.
2021.
Vertically distributed wall sources of buoyancy. Part 1. Unconfined.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
Ke, Junhao
Williamson, N.
Armfield, S.W.
Komiya, A.
and
Norris, S.E.
2021.
High Grashof number turbulent natural convection on an infinite vertical wall.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Parker, D. A.
Burridge, H. C.
Partridge, J. L.
Hacker, J. N.
and
Linden, P. F.
2021.
Vertically distributed wall sources of buoyancy. Part 2. Unventilated and ventilated confined spaces.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
Howland, Christopher J.
Ng, Chong Shen
Verzicco, Roberto
and
Lohse, Detlef
2022.
Boundary layers in turbulent vertical convection at high Prandtl number.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Chaigne, Martin
Berhanu, Michael
and
Kudrolli, Arshad
2023.
Dissolution-driven propulsion of floating solids.
Proceedings of the National Academy of Sciences,
Vol. 120,
Issue. 32,
He, Tianyi
Hu, Huijie
Tang, Ding
Chen, Xu
Meng, Jing
Cao, Yong
and
Lv, Xianqing
2023.
Experimental Study on the Effects of Waves and Current on Ice Melting.
Journal of Marine Science and Engineering,
Vol. 11,
Issue. 6,
p.
1209.
Wengrove, Meagan E.
Pettit, Erin C.
Nash, Jonathan D.
Jackson, Rebecca H.
and
Skyllingstad, Eric D.
2023.
Melting of glacier ice enhanced by bursting air bubbles.
Nature Geoscience,
Vol. 16,
Issue. 10,
p.
871.
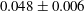 $0.048\pm 0.006$. We measure a maximum vertical plume velocity that follows the scaling predicted by Cooper & Hunt but is significantly smaller. Our measurements allow us to construct a turbulent plume model that predicts all plume properties at any height. We use this plume model to calculate plume widths, velocities and Reynolds numbers for typical dissolving icebergs and ice fronts and for a typical room with a heated or cooled vertical surface.
$0.048\pm 0.006$. We measure a maximum vertical plume velocity that follows the scaling predicted by Cooper & Hunt but is significantly smaller. Our measurements allow us to construct a turbulent plume model that predicts all plume properties at any height. We use this plume model to calculate plume widths, velocities and Reynolds numbers for typical dissolving icebergs and ice fronts and for a typical room with a heated or cooled vertical surface.