Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T07:42:30.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent wake past a three-dimensional blunt body. Part 2. Experimental sensitivity analysis

Published online by Cambridge University Press:  07 July 2014

M. Grandemange ,
M. Gohlke  and
O. Cadot
M. Grandemange
Affiliation:
Unité de Mécanique, Ecole Nationale Supérieure de Techniques Avancées, ParisTech, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France PSA Peugeot Citroën, Centre Technique de Vélizy, Route de Gisy, 78943 Vélizy-Villacoublay CEDEX, France
M. Gohlke
Affiliation:
PSA Peugeot Citroën, Centre Technique de Vélizy, Route de Gisy, 78943 Vélizy-Villacoublay CEDEX, France
O. Cadot*
Affiliation:
Unité de Mécanique, Ecole Nationale Supérieure de Techniques Avancées, ParisTech, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

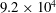The sensitivity of the flow around three-dimensional blunt geometry is investigated experimentally at Reynolds number $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}9.2\times 10^4$. Vertical and horizontal control cylinders are used to disturb the natural flow which is the superposition of two reflectional symmetry breaking states (see Part 1 of this study, Grandemange, Gohlke & Cadot, J. Fluid Mech., vol. 722, 2013b, pp. 51–84). When the perturbation breaks the symmetry of the set-up, it can select one of the two asymmetric topologies so that a mean side force is found. When the reflectional symmetry is preserved, some positions of horizontal and vertical control cylinders alter the natural bi-stability of the flow which may result in drag reduction. In addition, it is found that the horizontal perturbation affects the lift force especially when the top and bottom mixing layers are disturbed. The ability of the disturbances to suppress the bi-stable behaviour is discussed and, introducing a formalism of induced drag, a quantification of the impact on the drag of the cross-flow forces observed for the natural bi-stable wake is suggested. Finally, a general concept for a control strategy of separated flows past three-dimensional bluff bodies can be drawn up from these analyses.

JFM classification

Aerodynamics: Aerodynamics Wakes/Jets: Separated flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 439 - 461
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, S. R., Ramm, G. & Faitin, G.1984 Some salient features of the time-averaged ground vehicle wake. SAE Technical Paper Series 840300.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Beaudoin, J. F. & Aider, J. L. 2008 Drag and lift reduction of a three-dimensional bluff body using flaps. Exp. Fluids 44 (4), 491–501.Google Scholar
Beaudoin, J. F., Cadot, O., Aider, J. L., Gosse, K., Paranthoën, P., Hamelin, B., Tissier, M., Allano, D., Mutabazi, I. & Gonzalez, M. 2004 Cavitation as a complementary tool for automotive aerodynamics. Exp. Fluids 37 (5), 763–768.Google Scholar
Berger, E., Scholz, D. & Schumm, M. 1990 Coherent vortex structures in the wake of a sphere and a circular disk at rest and under forced vibrations. J. Fluids Struct. 4 (3), 231–257.Google Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2012a Reflectional symmetry breaking of the separated flow over three-dimensional bluff bodies. Phys. Rev. E 86, 035302.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013a Bi-stability in the turbulent wake past parallelepiped bodies with various aspect ratios and wall effects. Phys. Fluids 25, 095103.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013b Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.Google Scholar
Grandemange, M., Mary, A., Gohlke, M. & Cadot, O. 2013c Effect on drag of the flow orientation at the base separation of a simplified blunt road vehicle. Exp. Fluids 54 (5), 1–10.Google Scholar
Grandemange, M., Parezanović, V., Gohlke, M. & Cadot, O. 2012b On experimental sensitivity analysis of the turbulent wake from an axisymmetric blunt trailing edge. Phys. Fluids 24, 035106.CrossRefGoogle Scholar
Herry, B. B., Keirsbulck, L. & Paquet, J. B. 2011 Flow bi-stability downstream of three-dimensional double backward facing steps at zero-degree slideslip. Trans. ASME: J. Fluids Engng 133 (054501), 1–4.Google Scholar
Higuchi, H. 2005 Passive and active controls of three-dimensional wake of bluff body. JSME Intl J. B 48 (2), 322–327.Google Scholar
Hill, D. C.1992 A theoretical approach for analyzing the restabilization of wakes. NASA Tech. Rep. 103858.CrossRefGoogle Scholar
Lawson, N. J., Garry, K. P. & Faucompret, N. 2007 An investigation of the flow characteristics in the bootdeck region of a scale model notchback saloon vehicle. Proc. Inst. Mech. Engrs D 221 (D6), 739–754.Google Scholar
Lee, J. Y., Paik, B. G. & Lee, S. J. 2009 PIV measurements of hull wake behind a container ship model with varying loading condition. Ocean Engng 36 (5), 377–385.Google Scholar
Luchini, P., Giannetti, F. & Pralits, J. 2009 Structural sensitivity of the finite-amplitude vortex shedding behind a circular cylinder. In IUTAM Symposium on Unsteady Separated Flows and their Control, pp. 151–160. Springer.CrossRefGoogle Scholar
Magarvey, R. H. & Bishop, R. L. 1961 Transition ranges for three-dimensional wakes. Can. J. Phys. 39 (10), 1418–1422.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Meliga, P., Chomaz, J. & Sipp, D. 2009a Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.Google Scholar
Meliga, P., Chomaz, J. M. & Sipp, D. 2009b Unsteadiness in the wake of disks and spheres: instability, receptivity and control using direct and adjoint global stability analyses. J. Fluids Struct. 25 (4), 601–616.CrossRefGoogle Scholar
Meliga, P., Pujals, G. & Serre, E. 2012 Sensitivity of two-dimensional turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 24 (6), 061701.Google Scholar
Morrison, J. F. & Qubain, A. 2009 Control of an axisymmetric turbulent wake by a pulsed jet. In Advances in Turbulence XII, pp. 225–228.Google Scholar
Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83 (1), 80–83.Google Scholar
Parezanović, V. & Cadot, O. 2009 The impact of a local perturbation on global properties of a turbulent wake. Phys. Fluids 21, 071701.Google Scholar
Parezanović, V. & Cadot, O. 2012 Experimental sensitivity analysis of the global properties of a two-dimensional turbulent wake. J. Fluid Mech. 693, 115–149.CrossRefGoogle Scholar
Pier, B. 2008 Local and global instabilities in the wake of a sphere. J. Fluid Mech. 603, 39–61.Google Scholar
Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME: J. Fluids Engng 112, 386–392.Google Scholar
Sevilla, A. & Martinez-Bazan, C. 2004 Vortex shedding in high Reynolds number axisymmetric bluff body wakes: local linear instability and global bleed control. Phys. Fluids 16, 3460.Google Scholar
Siegel, S., Seidel, J., Cohen, K., Aradag, S. & McLaughlin, T.2008 Open loop transient forcing of an axisymmetric bluff body wake. AIAA Paper 2008-595.Google Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex shedding at low Reynolds numbers. J. Fluid Mech. 218, 71–107.Google Scholar
Szaltys, P., Chrust, M., Przadka, A., Goujon-Durand, S., Tuckerman, L. S. & Wesfreid, J. E. 2012 Nonlinear evolution of instabilities behind spheres and disks. J. Fluids Struct. 28, 483–487.Google Scholar
Wassen, E., Eichinger, S. & Thiele, F. 2010 Simulation of active drag reduction for a squareback vehicle. In Active Flow Control II, pp. 241–255.Google Scholar
Weickgenannt, A. & Monkewitz, P. A. 2000 Control of vortex shedding in an axisymmetric bluff body wake. Eur. J. Mech. (B/Fluids) 19 (5), 789–812.Google Scholar