Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T07:08:21.062Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent spot transit of a hypersonic laminar separation

Published online by Cambridge University Press:  31 January 2022

David Estruch-Samper Open the ORCID record for David Estruch-Samper [Opens in a new window] ,
Richard Hillier  and
Leon Vanstone Open the ORCID record for Leon Vanstone [Opens in a new window]
David Estruch-Samper*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK Performance and Aerodynamics, Reaction Engines, Abingdon OX14 3DB, UK
Richard Hillier
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
Leon Vanstone
Affiliation:
Aerospace Engineering Department, University of Texas at Austin, Austin, TX 78705, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

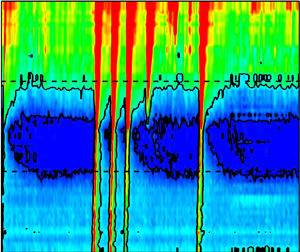
This paper presents an experimental study of the interaction of turbulent spots with an initially laminar separation, using schlieren visualisation and dynamic measurements of surface heat transfer and pressure. The separation is generated on a blunt cylinder-flare body, tested at Mach 9, and entropy layer effects result in a boundary layer edge Mach number of 3.43 at separation. A single roughness element is used to produce isolated spots, defined such that separation collapse and re-establishment is completed before arrival of the next spot. On average the spot axial length, at the start of the interaction, is 2.5 times the separation length, growing to 6.8 times as the spot base passes the original reattachment position. As such the spot comprises a large perturbation. The local separation responds almost immediately with passage of the spot, so that the downstream region may be unaffected while the upstream part has already collapsed. Re-establishment of separation is slow, taking up to four times the total transit time of the spot. A basic model is presented to explore the transient wave processes during spot passage.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Compressible boundary layers Compressible Flows: Hypersonic Flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 935 , 25 March 2022 , A25
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Babinsky, H. & Harvey, J.K. 2014 Shock Wave–Boundary-Layer Interactions. Cambridge Aerospace Series. Cambridge University Press.Google Scholar
Ben-Artzi, M. & Falcovitz, J. 1984 A second-order Godunov-type scheme for compressible fluid dynamics. J. Comput. Phys. 55, 1–32.10.1016/0021-9991(84)90013-5CrossRefGoogle Scholar
Berry, S.A. & Horvath, T.J. 2008 Discrete-roughness transition for hypersonic flight vehicles. J. Spacecr. Rockets 45, 216–227.10.2514/1.30970CrossRefGoogle Scholar
Butler, C. & Laurence, S.J. 2020 Interaction of hypersonic boundary-layer instability waves with axisymmetric compression and expansion corners. In Proc. AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020. AIAA Paper 2020-3071.Google Scholar
Casper, K.M., Beresh, S.J., Henfling, J.F., Spillers, R.W., Hunter, P. & Spitzer, S. 2018 Hypersonic fluid-structure interactions due to intermittent turbulent spots on a slender cone. AIAA J. 57 (2), 749–759.10.2514/1.J057374CrossRefGoogle Scholar
Casper, K.M., Beresh, S.J. & Schneider, S.P. 2014 Pressure fluctuations beneath instability wave packets and turbulent spots in a hypersonic boundary layer. J. Fluid Mech. 756, 1058–1091.10.1017/jfm.2014.475CrossRefGoogle Scholar
Chuvakhov, P.V., Fedorov, A.V. & Obraz, A.O. 2018 Numerical simulation of turbulent spots generated by unstable wave packets in a hypersonic boundary layer. Comput. Fluids 162, 26–38.10.1016/j.compfluid.2017.12.001CrossRefGoogle Scholar
Cook, W.J. & Felderman, E.J. 1966 Reduction of data from thin-film heat-transfer gauges: a concise numerical technique. AIAA J. 4, 561–562.10.2514/3.3486CrossRefGoogle Scholar
Denman, P.A. 1996 Experimental study of hypersonic boundary layers and base flows. PhD thesis, University of London.Google Scholar
Dwivedi, A., Sidharth, G.S., Nichols, J.W., Candler, G.V. & Jovanovic, M.R. 2019 Reattachment streaks in hypersonic compression ramp flow: an input–output analysis. J. Fluid Mech. 880, 113–135.10.1017/jfm.2019.702CrossRefGoogle Scholar
Emmons, H.W. 1951 The laminar-turbulent transition in a boundary layer. Part I. J. Aeronaut. Sci. 18 (7), 490–498.10.2514/8.2010CrossRefGoogle Scholar
Estruch-Samper, D., Hillier, R., Vanstone, L. & Ganapathisubramani, B. 2017 Effect of isolated roughness element height on high-speed laminar–turbulent transition. J. Fluid Mech. 818, R1.10.1017/jfm.2017.160CrossRefGoogle Scholar
European Space Agency (ESA) 2011 Skylon assessment report. Propulsion & Aerothermodynamics Division, Directorate of Technology, Engineering and Quality, ESA. TEC-MPC/2011/946/MF, pp. 1–52.Google Scholar
Fedorov, A. 2011 Transition and stability of high-speed boundary-layers. Annu. Rev. Fluid Mech. 818, 79–95.10.1146/annurev-fluid-122109-160750CrossRefGoogle Scholar
Fedorov, A. & Tumin, A. 2017 Receptivity of high-speed boundary layers to kinetic fluctuations. AIAA J. 55 (7), 2335–2348.10.2514/1.J055326CrossRefGoogle Scholar
Fiala, A., Hillier, R. & Estruch-Samper, D. 2014 Roughness-induced turbulent wedges in a hypersonic blunt-body boundary layer. J. Fluid Mech. 754, 208–231.10.1017/jfm.2014.388CrossRefGoogle Scholar
Fiala, A., Hillier, R., Mallinson, S.G. & Wijensinghe, H.S. 2006 Heat transfer measurement of turbulent spots in a hypersonic blunt-body boundary layer. J. Fluid Mech. 555, 81–111.10.1017/S0022112006009396CrossRefGoogle Scholar
Fischer, M.C. 1972 Spreading of a turbulent disturbance. AIAA J. 10, 957–959.10.2514/3.50265CrossRefGoogle Scholar
Franko, K.J. & Lele, S.K. 2013 Breakdown mechanisms and heat transfer overshoot in hypersonic zero pressure gradient boundary layers. J. Fluid Mech. 730, 491–532.10.1017/jfm.2013.350CrossRefGoogle Scholar
Gad-El-Hak, M., Blackwelder, R.F. & Riley, J.J. 1981 On the growth of turbulent regions in laminar boundary layers. J. Fluid Mech. 110, 73–95.10.1017/S002211208100061XCrossRefGoogle Scholar
Hader, C. & Fasel, H.F. 2019 Direct numerical simulations of hypersonic boundary-layer transition for a flared cone: fundamental breakdown. J. Fluid Mech. 869, 341–384.10.1017/jfm.2019.202CrossRefGoogle Scholar
Hein, S., Theiss, A., DI Giovanni, A., Stemmer, C., Schilden, T., Schroder, W., Paredes, P., Choudhari, M.M., LI, F. & Reshotko, E. 2019 Numerical investigation of roughness effects on transition on spherical capsules. J. Spacecr. Rockets 56 (2), 388–404.10.2514/1.A34247CrossRefGoogle ScholarPubMed
Hillier, R. 2007 Shock-wave/expansion-wave interactions and the transition between regular and Mach reflection. J. Fluid Mech. 575, 399–424.10.1017/S0022112006004083CrossRefGoogle Scholar
Horvath, T.J., Zalameda, J.N., Wood, W.A., Berry, S.A., Schwartz, R.J., Dantowitz, R.F., Spisz, T.S. & Taylor, J.C. 2012 Global infrared observations of roughness induced transition on the Space Shuttle orbiter. NATO RTO-MP-AVT-200, pp. 1–22.Google Scholar
Jackson, A.P., Hillier, R. & Soltani, S. 2001 Experimental and computational study of laminar cavity flows at hypersonic speeds. J. Fluid Mech. 427, 329–358.10.1017/S0022112000002433CrossRefGoogle Scholar
Jewell, J.S., Leyva, I.A. & Shepherd, J.E. 2017 Turbulent spots in hypervelocity flow. Exp. Fluids 58, 32.10.1007/s00348-017-2317-yCrossRefGoogle Scholar
Juliano, T.J., Jewell, J.S., Kimmel, R.L. 2021 HIFiRE-5b boundary-layer transition length and turbulent overshoot. J. Spacecr. Rockets 58 (2), 265–283.10.2514/1.A34856CrossRefGoogle Scholar
Keyes, F.G. 1952 The heat conductivity, viscosity, specific heat and Prandtl numbers for thirteen gases. Tech. Rep. 37. Massachussetts Institute of Technology, Project Squid.Google Scholar
Kimmel, R.L., Adamczak, D.W., Hartley, D., Alesi, H., Frost, M.A., Pietsch, R., Shannon, J. & Silvester, T. 2018 Hypersonic international flight research experimentation-5b flight overview. J. Spacecr. Rockets 55 (6), 1303–1314.10.2514/1.A34148CrossRefGoogle Scholar
Krishnan, L. & Sandham, N.D. 2006 Effect of Mach number on the structure of turbulent spots. J. Fluid Mech. 566, 225–234.10.1017/S0022112006002412CrossRefGoogle Scholar
Krishnan, L. & Sandham, N.D. 2007 Strong interaction of a turbulent spot with a shock-induced separation bubble. Phys. Fluids 19, 016102.10.1063/1.2432158CrossRefGoogle Scholar
Laderman, A.J. 1980 Adverse pressure gradient effects on supersonic boundary-layer turbulence. AIAA J. 18, 1186–1195.10.2514/3.50870CrossRefGoogle Scholar
Lee, C. & Jiang, X. 2019 Flow structures in transitional and turbulent boundary layers. Phys. Fluids 31, 111301.Google Scholar
Leidy, A.N., Reshotko, E., Siddiqui, F. & Bowersox, R.D.W. 2017 Transition due to roughness on blunt capsule: comparison with transient growth correlation. J. Spacecr. Rockets 55 (1), 167–180.10.2514/1.A33625CrossRefGoogle Scholar
Mack, L.M. 1984 Boundary layer linear stability theory. In Special Course on Stability and Transition of Laminar Flow. AGARD Rep. 709, vol. 3, pp. 1–81.Google Scholar
Mallinson, S.G., Hillier, R., Jackson, A.P., Kirk, D.C., Soltani, S. & Zanchetta, M. 2000 Gun tunnel flow calibration: defining input conditions for hypersonic flow computations. Shock Waves 10, 313–322.10.1007/s001930000064CrossRefGoogle Scholar
Mee, D.J. 2002 Boundary-layer transition measurements in hypervelocity flows in a shock tunnel. AIAA J. 40, 1542–1548.10.2514/2.1851CrossRefGoogle Scholar
Murray, N., Hillier, R. & Williams, S. 2013 Experimental investigation of axisymmetric hypersonic shock-wave/turbulent-boundary-layer interactions. J. Fluid Mech. 714, 152–189.10.1017/jfm.2012.464CrossRefGoogle Scholar
Narasimha, R. 1985 The laminar-turbulent transition zone in the turbulent boundary layer. Prog. Aerosp. Sci. 22, 29–80.10.1016/0376-0421(85)90004-1CrossRefGoogle Scholar
Novikov, A., Egorov, I. & Fedorov, A. 2016 Direct numerical simulation of wave packets in hypersonic compression-corner flow. AIAA J. 54 (7), 2034–2050.10.2514/1.J054665CrossRefGoogle Scholar
Paredes, P., Choudhari, M. & Li, F. 2020 a Mechanism for frustum transition over blunt cones at hypersonic speeds. J. Fluid Mech. 894, A22.10.1017/jfm.2020.261CrossRefGoogle Scholar
Paredes, P., Choudhari, M., Li, F., Jewell, J.S., Kimmel, R.L., Marineau, E.C. & Grossir, G. 2020 b Nosetip bluntness effects on transition at hypersonic speeds: experimental and numerical analysis. Chapter 7 in Hypersonic Boundary-Layer Transition Prediction. NATO Tech. Rep. NTO-STO-TR-AVT-240, pp. 1–36.Google Scholar
Perry, A.E., Lim, T.T. & Teh, E.W. 1981 A visual study of turbulent spots. J. Fluid Mech. 104, 387–405.10.1017/S0022112081002966CrossRefGoogle Scholar
Radespiel, R., Ali, S.R.C., Munoz, F., Bowersox, R., Leidy, A., Tanno, H., Kirk, L.C. & Reshotko, E. 2018 Experimental investigation of roughness effects on transition on blunt spherical capsule shapes. J. Spacecr. Rockets 56 (2), 405–420.10.2514/1.A34295CrossRefGoogle Scholar
Redford, J.A., Sandham, N.D. & Roberts, G.T. 2012 Numerical simulations of turbulent spots in supersonic boundary layers: effects of Mach number and wall temperature. Prog. Aerosp. Sci. 52, 67–79.10.1016/j.paerosci.2011.08.002CrossRefGoogle Scholar
Reshotko, E. 2001 Transient growth: a factor in bypass transition. Phys. Fluids 13 (5), 1067–1075.10.1063/1.1358308CrossRefGoogle Scholar
Robbins, B.A., Casper, K.M. & Mesh, M. 2019 Quantifying the structural response of a slender cone to turbulent spots at Mach 6. In Proc. AIAA Scitech 2019 Forum, 7–11 January 2019, San Diego, California, USA. AIAA Paper 2019-1631.Google Scholar
Roshko, A. & Thomke, G.J. 1966 Observations of turbulent reattachment behind an axisymmetric downstream-facing step in supersonic flow. AIAA J. 4 (6), 975–980.10.2514/3.3590CrossRefGoogle Scholar
Schneider, S.P. 2008 Effects of roughness on hypersonic boundary-layer transition. J. Spacecr. Rockets 45 (2), 193–209.10.2514/1.29713CrossRefGoogle Scholar
Schultz, D.L. & Jones, T.V. 1973 Heat-transfer measurements in short-duration hypersonic facilities. AGARDograph 165.Google Scholar
Seifert, A. & Wygnansky, L. 1995 On turbulent spots in a laminar boundary layer subjected to a self-similar adverse pressure gradient. J. Fluid Mech. 296, 185–209.10.1017/S0022112095002102CrossRefGoogle Scholar
Sivasubramanian, J. & Fasel, H.F. 2015 Direct numerical simulation of transition in a sharp cone boundary layer at Mach 6: fundamental breakdown. J. Fluid Mech. 768, 175–218.10.1017/jfm.2014.678CrossRefGoogle Scholar
Tumin, A. 2007 Outlook for theoretical modelling of isolated roughness-induced perturbations in turbulent boundary layers. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, 25–28 June 2007, Miami, FL, USA. AIAA Paper 2007-3993.Google Scholar
Tumin, A. 2008 Nonparallel flow effects on roughness-induced perturbations in boundary layers. J. Spacecr. Rockets 45 (6), 1176–1184.10.2514/1.37136CrossRefGoogle Scholar
Whalen, T.J., Schoneich, A.G., Laurence, S.J., Sullivan, B.T., Bodony, D.J., Freydin, M., Dowell, E.H. & Buck, G.M. 2020 Hypersonic fluid-structure interactions in compression corner shock-wave/boundary-layer interaction. AIAA J. 58 (9), 4090–4105.10.2514/1.J059152CrossRefGoogle Scholar
Wheaton, B.M., Bartkowicz, M.D., Subbareddy, P.K., Schneider, S.P. & Candler, G.V. 2011 Roughness-induced instabilities at Mach 6: a combined numerical and experimental study. In Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit, 27–30 June 2011, Honolulu, Hawaii, USA. AIAA Paper 2011-3248.Google Scholar
Wheaton, B.M., Berridge, D.C., Wolf, T., Araya, D., Stevens, R., Mcgrath, B.E., Kemp, B. & Adamczak, D. 2021 Final design of the Boundary Layer Transition (BOLT) flight experiment. J. Spacecr. Rockets 58 (1), 6–17.10.2514/1.A34809CrossRefGoogle Scholar