Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T15:39:00.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics

Published online by Cambridge University Press:  07 March 2012

B. J. Balakumar ,
G. C. Orlicz ,
J. R. Ristorcelli ,
S. Balasubramanian ,
K. P. Prestridge  and
C. D. Tomkins
B. J. Balakumar*
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
G. C. Orlicz
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
J. R. Ristorcelli
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
S. Balasubramanian
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
K. P. Prestridge
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
C. D. Tomkins
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The properties of turbulent mixing in a Richtmyer–Meshkov (RM) unstable fluid layer are studied under the impact of a single shock followed by a reshock wave using simultaneous velocity–density measurements to provide new insights into the physics of RM mixing. The experiments were conducted on a varicose 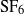fluid layer (heavy fluid) interposed in air (light fluid) inside a horizontal shock tube at an incident Mach number of 1.21 and a reflected reshock Mach number of 1.14. The light–heavy–light fluid layer is observed to develop a nonlinear growth pattern, with no transition to turbulence upon impact by a single shock (up to 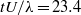). However, upon reshock, enhanced mixing between the heavy and light fluids along with a transition to a turbulent state characterized by the generation of significant turbulent velocity fluctuations (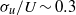) is observed. The streamwise and spanwise root-mean-squared velocity fluctuation statistics show similar trends across the fluid layer after reshock, with no observable preference for the direction of the shock wave motion. The measured streamwise mass flux (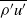) shows opposing signs on either side of the density peak within the fluid layer, consistent with the turbulent material transport being driven along the direction of the density gradient. Measurements of three of the six independent components of the general Reynolds stress tensor () show that the self-correlation terms 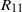and are similar in magnitude across much of the fluid layer, and much larger than the cross-correlation term 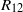. Most importantly, the Reynolds stresses (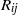) are dominated by the mean density, cross-velocity product term (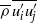), with the mass flux product and triple correlation terms being negligibly smaller in comparison. A lack of homogeneous mixing (and, possibly, a long-term imprint of the initial conditions) is observed in the spanwise turbulent mass flux measurements, with important implications for the simulation and modelling of RM mixing flows.

JFM classification

Instability: Nonlinear instability Compressible Flows: Shock waves Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 67 - 93
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abarzhi, S. I. 2010 On fundamentals of Rayleigh–Taylor turbulent mixing. Europhys. Lett. 91, 35001.CrossRefGoogle Scholar
2. Adrian, R. J. & Westerweel, J. 2010 Particle Image Velocimetry. Cambridge University Press.Google Scholar
3. Aglitskiy, Y., Velikovich, A. L., Karasik, M., Metzler, N., Zalesak, S. T., Schmitt, A. J., Philips, L., Gardner, J. H., Serlin, V., Weaver, J. L. & Obenschain, S. P. 2010 Basic hydrodynamics of Richtmyer–Meshkov-type growth and oscillations in the inertial confinement fusion-relevant conditions. Phil. Trans. R. Soc. A 368, 1739–1768.CrossRefGoogle ScholarPubMed
4. Arnett, W. D., Bahcall, J. N., Kirshner, R. P. & Woosley, S. E. 1987 Supernova 1987a. Annu. Rev. Astron. Astrophys. 27, 629–700.CrossRefGoogle Scholar
5. Balakumar, B. J., Orlicz, G. C., Tomkins, C. D. & Prestridge, K. P. 2008 Simultaneous particle-image velocimetry–planar laser-induced fluorescence measurements of Richtmyer–Meshkov instability growth in a gas curtain with and without reshock. Phys. Fluids 20 (12), 124103.CrossRefGoogle Scholar
6. Balasubramanian, S., Orlicz, G., Prestridge, K. P. & Balakumar, B. J. 2011 Influence of initial conditions on turbulent mixing in shock driven Richtmyer–Meshkov flows, AIAA Paper 2011-3710.CrossRefGoogle Scholar
7. Banerjee, A., Gore, R. A. & Andrews, M. J. 2010a Development and validation of a turbulent-mix model for variable density and compressible flows. Phys. Rev. E 82, 046309.CrossRefGoogle ScholarPubMed
8. Banerjee, A., Kraft, W. N. & Andrews, M. J. 2010b Detailed measurements of a statistically steady Rayleigh–Taylor mixing layer from small to high Atwood numbers. J. Fluid Mech. 659, 127–190.CrossRefGoogle Scholar
9. Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22, 130–136.CrossRefGoogle Scholar
10. Besnard, D., Harlow, F. H., Rauenzahn, R. M. & Zemach, C. 1992 Turbulence transport equations for variable-density turbulence and their relationship to two-field models. Tech. Rep. LA-12303-MS. Los Alamos National Laboratory.CrossRefGoogle Scholar
11. Bevington, P. R. 1969 Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill.Google Scholar
12. Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence. Kluwer Academic.CrossRefGoogle Scholar
13. Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–363.CrossRefGoogle Scholar
14. Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
15. Gowardhan, A., Balasubramanian, S., Grinstein, F. F., Prestridge, K. & Ristorcelli, R. 2011 Analysis of computational and laboratory shocked gas-curtain experiments. AIAA Paper 2011-3040.CrossRefGoogle Scholar
16. Gowardhan, A. & Grinstein, F. 2010 Simulation of material mixing in shocked and reshocked gas-curtain experiments. In Bulletin of the American Physical Society, Division of Fluid Dynamics Meeting, 21–23 November 2010, Long Beach, CA. APS.Google Scholar
17. Gowardhan, A. A., Grinstein, F. F. & Wachtor, A. J. 2010 Three dimensional simulations of Richtmyer–Meshkov instabilities in shock tube experiments. AIAA Paper 2010-1075.CrossRefGoogle Scholar
18. Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.CrossRefGoogle Scholar
19. Hinze, J. O. 1959 Turbulence. McGraw-Hill.Google Scholar
20. Jacobs, J. W., Jenkins, D. G., Klein, D. L. & Benjamin, R. F. 1995 Nonlinear growth of the shock-accelerated instability of a thin fluid layer. J. Fluid Mech. 295, 23–42.CrossRefGoogle Scholar
21. Jourdan, G., Schwaederle, L., Houas, L., Haas, J.-F., Aleshin, A. N., Sergeev, S. V. & Zaytsev, S. G. 2001 Hot-wire method for measurements of turbulent mixing induced by Richtmyer–Meshkov instability in shock tube. Shock Waves 11, 189–197.CrossRefGoogle Scholar
22. von Kármán, T. 1938 Some remarks on the statistical theory of turbulence. In Proceedings of the Fifth International Congress for Applied Mechanics, 12–16 September 1938, Cambridge, MA (ed. den Hartog, J. P. & Peters, H. ). John Wiley and Sons Inc., New York, NY (USA) & Chapman and Hall Ltd, London (UK), 1939.Google Scholar
23. Latini, M., Schilling, O. & Don, W. S. 2007 High-resolution simulations and modelling of reshocked single-mode Richtmyer–Meshkov instability: comparison to experimental data and to amplitude growth model predictions. Phys. Fluids 19, 024104.CrossRefGoogle Scholar
24. Livescu, D. & Ristorcelli, J. R. 2007 Buoyancy-driven variable-density turbulence. J. Fluid Mech. 591, 43–71.CrossRefGoogle Scholar
25. Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.CrossRefGoogle Scholar
26. Livescu, D., Ristorcelli, J. R., Gore, R. A., Dean, S. H., Cabot, W. H. & Cook, A. W. 2009 High-Reynolds number Rayleigh–Taylor turbulence. J. Turbul. 10 (13), 1–32.CrossRefGoogle Scholar
27. Mariani, C., Jourdan, G., Houas, L. & Schwaederle, L. 2009 Hot wire, laser Doppler measurements and visualization of shock induced turbulent mixing zones. Shock Waves 18, 1181–1186.CrossRefGoogle Scholar
28. Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13, 735.CrossRefGoogle Scholar
29. Maurel, A., Ern, P., Zielinska, B. J. A. & Wesfreid, J. E. 1996 Experimental study of self-sustained oscillations in a confined jet. Phys. Rev. E 54, 3643–3651.CrossRefGoogle Scholar
30. Nishihara, K., Wouchuk, J. G., Matsuoka, C., Ishizaki, R. & Zhakhovsky, V. V. 2010 Richtmyer–Meshkov instability: theory of linear and nonlinear evolution. Phil. Trans. R. Soc. A 368, 1769–1807.CrossRefGoogle ScholarPubMed
31. Orlicz, G. C., Balakumar, B. J., Tomkins, C. D. & Prestridge, K. P. 2009 A Mach number study of the Richtmyer–Meshkov instability in a varicose, heavy-gas curtain. Phys. Fluids 21, 064102.CrossRefGoogle Scholar
32. Orlov, S. S., Abarzhi, S., Oh, S. B., Barbastathis, G. & Sreenivasan, K. R. 2010 High-performance holographic technologies for fluid-dynamics experiments. Phil. Trans. R. Soc. A 368, 1705–1737.CrossRefGoogle ScholarPubMed
33. Poggi, F., Thorembey, M. H. & Rodriguez, G. 1998 Velocity measurements in turbulent gaseous mixtures induced by Richtmyer–Meshkov instability. Phys. Fluids 10 (11), 2698–2700.CrossRefGoogle Scholar
34. Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
35. Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.CrossRefGoogle Scholar
36. Robey, H. F., Zhou, Y., Buckingham, A. C., Keiter, P., Remington, B. A. & Drake, R. P. 2003 The time scale for the transition to turbulence in a high Reynolds number, accelerated flow. Phys. Plasmas 10 (3), 614–622.CrossRefGoogle Scholar
37. Ryutov, D., Drake, R. P., Kane, J., Liang, E., Remington, B. A. & Wood-Vasey, W. M. 1999 Similarity criteria for the laboratory simulation of supernova hydrodynamics. Astrophys. J. 518 (2), 821–832.CrossRefGoogle Scholar
38. Soloff, S. M., Adrian, R. J. & Liu, Z. C. 1997 Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 8 (12), 1441–1454.CrossRefGoogle Scholar
39. Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2010 The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 654, 99–139.CrossRefGoogle Scholar
40. Tomkins, C., Kumar, S., Orlicz, G. & Prestridge, K. 2008 An experimental investigation of mixing mechanisms in shock-accelerated flow. J. Fluid Mech. 611, 131–150.CrossRefGoogle Scholar
41. Velikovich, A. L., Dahlburg, J. P., Schmitt, A. J., Gardner, J. H., Phillips, L., Cochran, F. L., Chong, Y. K., Dimonte, G. & Metzler, N. 2000 Richtmyer–Meshkov-like instabilities and early-time perturbation growth in laser targets and Z-pinch loads. Phys. Plasmas 7 (5), 1662–1671.CrossRefGoogle Scholar
42. Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
43. Yang, J., Kubota, T. & Zukoski, E. E. 1993 Applications of shock-induced mixing to supersonic combustion. AIAA J. 31 (5), 854–862.CrossRefGoogle Scholar
44. Zabusky, N. J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31, 495–536.CrossRefGoogle Scholar
45. Zoldi-Sood, C., Gore, R., Balakumar, B. J., Orlicz, G., Ranjan, D., Tomkins, C. & Prestridge, K. 2008 Simulations of a reshocked varicose gas curtain. In Bulletin of the American Physical Society, Division of Fluid Dynamics Meeting, 23–25 November 2008, San Antonio, TX. APS.Google Scholar