Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T14:11:35.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent mixing driven by spherical implosions. Part 2. Turbulence statistics

Published online by Cambridge University Press:  28 April 2014

M. Lombardini ,
D. I. Pullin  and
D. I. Meiron
M. Lombardini*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
D. I. Meiron
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present large-eddy simulations (LES) of turbulent mixing at a perturbed, spherical interface separating two fluids of differing densities and subsequently impacted by a spherically imploding shock wave. This paper focuses on the differences between two fundamental configurations, keeping fixed the initial shock Mach number $\approx $1.2, the density ratio (precisely 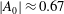$|A_0|\approx 0.67$) and the perturbation shape (dominant spherical wavenumber 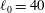$\ell _0=40$ and amplitude-to-initial radius of 3 %): the incident shock travels from the lighter fluid to the heavy one, or inversely, from the heavy to the light fluid. In Part 1 (Lombardini, M., Pullin, D. I. & Meiron, D. I., J. Fluid Mech., vol. 748, 2014, pp. 85–112), we described the computational problem and presented results on the radially symmetric flow, the mean flow, and the growth of the mixing layer. In particular, it was shown that both configurations reach similar convergence ratios $\approx $2. Here, turbulent mixing is studied through various turbulence statistics. The mixing activity is first measured through two mixing parameters, the mixing fraction parameter 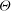$\varTheta $ and the effective Atwood ratio 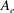$A_e$, which reach similar late time values in both light–heavy and heavy–light configurations. The Taylor-scale Reynolds numbers attained at late times are estimated at approximately 2000 in the light–heavy case and 1000 in the heavy–light case. An analysis of the density self-correlation 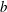$b$, a fundamental quantity in the study of variable-density turbulence, shows asymmetries in the mixing layer and non-Boussinesq effects generally observed in high-Reynolds-number Rayleigh–Taylor (RT) turbulence. These traits are more pronounced in the light–heavy mixing layer, as a result of its flow history, in particular because of RT-unstable phases (see Part 1). Another measure distinguishing light–heavy from heavy–light mixing is the velocity-to-scalar Taylor microscales ratio. In particular, at late times, larger values of this ratio are reported in the heavy–light case. The late-time mixing displays the traits some of the traits of the decaying turbulence observed in planar Richtmyer–Meshkov (RM) flows. Only partial isotropization of the flow (in the sense of turbulent kinetic energy (TKE) and dissipation) is observed at late times, the Reynolds normal stresses (and, thus, the directional Taylor microscales) being anisotropic while the directional Kolmogorov microscales approach isotropy. A spectral analysis is developed for the general study of statistically isotropic turbulent fields on a spherical surface, and applied to the present flow. The resulting angular power spectra show the development of an inertial subrange approaching a Kolmogorov-like 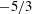$-5/3$ power law at high wavenumbers, similarly to the scaling obtained in planar geometry. It confirms the findings of Thomas & Kares (Phys. Rev. Lett., vol. 109, 2012, 075004) at higher convergence ratios and indicates that the turbulent scales do not seem to feel the effect of the spherical mixing-layer curvature.

JFM classification

Turbulent Flows: Compressible turbulence Compressible Flows: Shock waves Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 113 - 142
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balakrishnan, K. & Menon, S. 2011 Characterization of the mixing layer resulting from the detonation of heterogeneous explosive charges. Flow Turbul. Combust. 87, 639–671.Google Scholar
Besnard, D., Harlow, F. H., Rauenzahn, R. M. & Zemach, C.1992 Turbulent transport equations for variable-density turbulence and their relationship to two-fluid models. LANL Tech. Rep. LA-12303-MS.Google Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type Ia supernovae. Nat. Phys. 2 (8), 562–568.CrossRefGoogle Scholar
Chung, D. & Pullin, D. I. 2010 Direct numerical simulation and large-eddy simulation of stationary buoyancy-driven turbulence. J. Fluid Mech. 643, 279–308.Google Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Glimm, J., Grove, J. W., Zhang, Y. & Dutta, S. 2002 Numerical study of axisymmetric Richtmyer–Meshkov instability and azimuthal effect on spherical mixing. J. Stat. Phys. 107 (1/2), 241–260.Google Scholar
Gotoh, T., Watanabe, T. & Suzuki, Y. 2011 Universality and anisotropy in passive scalar fluctuations in turbulence with uniform mean gradient. J. Turbul. 12, N48.Google Scholar
Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multi-scale modeling of Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.Google Scholar
Hill, D. J. & Pullin, D. I. 2004 Hybrid tuned center-difference–WENO method for large eddy simulations in the presence of strong shocks. J. Comput. Phys. 194 (2), 435–450.Google Scholar
Honein, A. E. & Moin, P. 2004 Higher entropy conservation and numerical stability of compressible turbulence simulations. J. Comput. Phys. 201 (2), 531–545.Google Scholar
Joggerst, C. C., Almgren, A. & Woosley, S. E. 2010 Three-dimensional simulations of Rayleigh–Taylor mixing in core-collapse supernovae. Astrophys. J. 723, 353–363.Google Scholar
Johnsen, E., Larsson, J., Bhagatwala, A. V., Cabot, W. H., Moin, P., Olson, B. J., Rawat, P. S., Shankar, S. K., Sjögreen, B., Yee, H. C., Zhong, X. & Lele, S. K. 2010 Assessment of high-resolution methods for numerical simulations of compressible turbulence with shock waves. J. Comput. Phys. 229, 1213–1237.Google Scholar
Kosovic, B., Pullin, D. I. & Samtaney, R. 2002 Subgrid-scale modeling for large-eddy simulations of compressible turbulence. Phys. Fluids 14 (4), 1511–1522.CrossRefGoogle Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2007 Buoyancy-driven variable-density turbulence. J. Fluid Mech. 591, 43–71.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2009 Mixing asymmetry in variable density turbulence. In Advances in Turbulence XII (ed. Eckhardt, B.), Springer Proceedings in Physics, vol. 132, pp. 545–548. Springer.Google Scholar
Livescu, D., Ristorcelli, J. R., Gore, R. A., Dean, S. H., Cabot, H. W. & Cook, A. W. 2009 High Reynolds number Rayleigh–Taylor turbulence. J. Turbul. 10 (13), 1–32.CrossRefGoogle Scholar
Lombardini, M.2008 Richtmyer–Meshkov instability in converging geometries. PhD thesis, California Institute of Technology. http://thesis.library.caltech.edu/2319/.Google Scholar
Lombardini, M., Deiterding, R. & Pullin, D. I. 2008 Large-eddy simulation of the Richtmyer–Meshkov instability in a converging geometry. In Quality and Reliability of Large-Eddy Simulations, Proc. of QLES 2007 Intl Symposium (ed. Meyers, J., Geurts, B. J. & Sagaut, P.), ERCOFTAC Series, vol. 12, pp. 23–51. Springer.Google Scholar
Lombardini, M., Hill, D. J., Pullin, D. I. & Meiron, D. I. 2011 Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 670, 439–480.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2014 Turbulent mixing driven by spherical implosions. Part 1. Flow description and mixing-layer growth. J. Fluid Mech. 748, 85–112.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Sov. Fluid Dyn. 4 (5), 101–108.Google Scholar
Overholt, M. R. & Pope, S. B. 1996 Direct numerical simulation of a passive scalar with imposed mean gradient in isotropic turbulence. Phys. Fluids 8, 3128–3148.Google Scholar
Pomraning, E. & Rutland, C. J. 2002 Dynamic one-equation nonviscosity large-eddy simulation model. AIAA J. 40 (4), 689–701.CrossRefGoogle Scholar
Pullin, D. I. 2000 A vortex-based model for the subgrid flux of a passive scalar. Phys. Fluids 12 (9), 2311–2319.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.Google Scholar
Ristorcelli, J. R. 2006 Passive scalar mixing: analytic study of time scale ratio, variance, and mix rate. Phys. Fluids 18, 124103.Google Scholar
Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Thomas, V. A. & Kares, R. J. 2012 Drive asymmetry and the origin of turbulence in an ICF implosion. Phys. Rev. Lett. 109 (7), 075004.Google Scholar
Wachtor, A. J., Grinstein, F. F., DeVore, C. R., Ristorcelli, J. R. & Margolin, J. G. 2013 Implicit large-eddy simulation of passive scalar mixing in statistically stationary isotropic turbulence. Phys. Fluids 25 (2), 025101.Google Scholar
Warhaft, Z. & Lumley, J. L. 1978 An experimental study of the decay of temperature fluctuations in grid-generated turbulence. J. Fluid Mech. 88, 659–684.Google Scholar
Welser-Sherrill, L., Haynes, D. A., Mancini, R. C., Cooley, J. H., Tommasini, R., Golovkin, I. E., Sherrill, M. E. & Haan, S. W. 2008 Inference of ICF implosion core mix using experimental data and theoretical mix modeling. High Energy. Dens. Phys. 5 (4), 249–257.Google Scholar
Youngs, D. L. 1994 Numerical simulations of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 12, 725–750.Google Scholar
Youngs, D. L. & Williams, R. J. R. 2008 Turbulent mixing in spherical implosions. Intl J. Numer. Meth. Fluids 56 (8), 1597–1603.CrossRefGoogle Scholar