Hostname: page-component-6587cd75c8-9kljr Total loading time: 0 Render date: 2025-04-24T09:45:56.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flow of non-Newtonian fluid in rough channels

Published online by Cambridge University Press:  27 November 2024

C. Narayanan Open the ORCID record for C. Narayanan [Opens in a new window] ,
J.S. Singh ,
S. Nauer ,
R.J. Belt Open the ORCID record for R.J. Belt [Opens in a new window] ,
T. Palermo  and
D. Lakehal Open the ORCID record for D. Lakehal [Opens in a new window]
C. Narayanan
Affiliation:
AFRY AMS, Herostrasse 12, 8048 Zürich, Switzerland
J.S. Singh
Affiliation:
AFRY AMS, Herostrasse 12, 8048 Zürich, Switzerland
S. Nauer
Affiliation:
AFRY AMS, Herostrasse 12, 8048 Zürich, Switzerland
R.J. Belt
Affiliation:
TotalEnergies, Pôle d'Etudes et de Recherche de Lacq (PERL), Pôle Economique 2 – B.P. 47, 64170 Lacq, France
T. Palermo
Affiliation:
TotalEnergies, Pôle d'Etudes et de Recherche de Lacq (PERL), Pôle Economique 2 – B.P. 47, 64170 Lacq, France
D. Lakehal*
Affiliation:
AFRY AMS, Herostrasse 12, 8048 Zürich, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

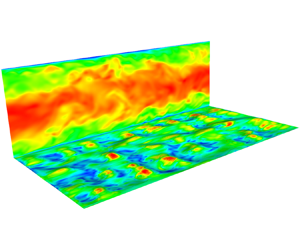
Direct numerical simulations of the turbulence of a Herschel–Bulkley (HB) fluid in a rough channel are performed at a shear Reynolds number $Re_{\tau } \approx 300$ and a Bingham number ${Bn} \approx 0.9$. For the type of rough surface used in this study, the results indicate that Townsend's wall similarity hypothesis also holds for HB fluids. However, there are notable differences compared with the effect of roughness on Newtonian fluids. More specifically, the effect of roughness appears to be slightly stronger for HB fluids, in the sense that the bulk Reynolds number, based on the viscosity at the wall, is reduced further due to the increase in viscosity in the troughs of the roughness surface induced by the low shear. At the same time, for the simulated rough surface, the contribution of form drag to the total pressure drop is reduced from 1/4 to about 1/5 due to the persistence of viscous shear in the boundary layer, reducing its shielding effect. As for the friction factor, due to the nonlinearity of the HB constitutive relation, its use with the wall shear rate from the mean wall shear stress underpredicts the minimum viscosity at the wall by up to 18 %. This inevitably leads to uncertainties in the prediction of the friction factor. Finally, it is observed that the rough surface is unable to break the peculiar near-wall flow structure of HB fluids, which consists of long persistent low-speed streaks occupying the entire domain. This means that the small-scale energy is significantly reduced for HB fluids, even in rough channels, with the energy more concentrated in the lower wavenumber range, implying an increase in the slope of the power spectrum to $-7/2$ in the inertial range, as shown by Mitishita et al. (J. Non-Newtonian Fluid Mech., vol. 293, 2021, 104570).

JFM classification

Complex Fluids: Complex Fluids Boundary Layers: Boundary Layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A55
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdelgawad, M.S., Cannon, I. & Rosti, M.E. 2023 Scaling and intermittency in turbulent flows of elastoviscoplastic fluids. Nat. Phys. 19, 1059–1063.CrossRefGoogle Scholar
Anbarlooei, H.R., Cruz, D.O.A., Ramos, F., Santos, C.M.M. & Silva Freire, A.P. 2018 On the connection between Kolmogorov microscales and friction in pipe flows of viscoplastic fluids. Physica D 376–377, 69–77.CrossRefGoogle Scholar
Arosemena, A.A., Andersson, H.I. & Solsvik, J. 2021 Turbulent channel flow of generalized Newtonian fluids at a low Reynolds number. J. Fluid Mech. 908, A43.CrossRefGoogle Scholar
Balmforth, N.J., Frigaard, I.A. & Ovarlez, G. 2014 Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46, 121–146.CrossRefGoogle Scholar
Beckermann, C., Diepers, H.-J., Steinbach, I., Karma, A. & Tong, X. 1999 Modeling melt convection in phase-field simulations of solidification. J. Comput. Phys. 154 (2), 468–496.CrossRefGoogle Scholar
Busse, A., Thakkar, M. & Sandham, N.D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.CrossRefGoogle Scholar
Chatzikyriakou, D., Buongiorno, J., Caviezel, D. & Lakehal, D. 2015 DNS and LES of turbulent flow in a closed channel featuring a pattern of hemispherical roughness elements. Intl J. Heat Fluid Flow 53, 29–43.CrossRefGoogle Scholar
Chung, D., Hutchins, N., Schultz, M.P. & Flack, K.A. 2021 Predicting the drag of rough surfaces. Annu. Rev. Fluid Mech. 53, 439–471.CrossRefGoogle Scholar
Dubief, Y., White, C.M., Rerrapon, V.E., Shaqfeh, E.S.G., Moin, P. & Lele, S.K. 2004 On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.CrossRefGoogle Scholar
Durbin, P.A., Medic, G., Seo, J.-M., Eaton, J.K. & Song, S. 2001 Rough wall modification of two-layer k-$\varepsilon$. Trans. ASME J. Fluids Engng 123 (1), 16–21.CrossRefGoogle Scholar
Escudier, M.P., Nickson, A.K. & Poole, R.J. 2009 Turbulent flow of viscoelastic shear-thinning liquids through a rectangular duct: quantification of turbulence anisotropy. J. Non-Newtonian Fluid Mech. 160 (1), 2–10.CrossRefGoogle Scholar
Esmael, A. & Nouar, C. 2008 Transitional flow of a yield-stress fluid in a pipe: evidence of a robust coherent structure. Phys. Rev. E 77 (5), 057302.CrossRefGoogle Scholar
Esmael, A., Nouar, C., Lefevre, A. & Kabouya, N. 2010 Transitional flow of a non-Newtonian fluid in a pipe: experimental evidence of weak turbulence induced by shear-thinning behavior. Phys. Fluids 22 (10), 101701.CrossRefGoogle Scholar
Fulgosi, M., Lakehal, D., Banerjee, S. & DeAngelis, V. 2003 Direct numerical simulation of turbulence in a sheared air–water flow with deformable interface. J. Fluid Mech. 482, 310.CrossRefGoogle Scholar
Gampert, B. & Yong, C. 1990 The influence of polymer additives on the coherent structure of turbulent channel flow. In Structure of Turbulence and Drag Reduction (ed. A. Gyr), pp. 223–232. Springer.CrossRefGoogle Scholar
Gavrilov, A. & Rudyak, V. 2016 Direct numerical simulation of the turbulent flows of power-law fluids in a circular pipe. Thermophys. Aeromech. 23, 473–486.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, stream and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center For Turbulence Research.Google Scholar
Izbassarov, D., Rosti, M.E., Brandt, L. & Tammisola, O. 2021 Effect of finite Weissenberg number on turbulent channel flows of an elastoviscoplastic fluid. J. Fluid Mech. 927, A45.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Karahan, D., Ranjan, D. & Aidun, C. 2023 Turbulent channel flow of generalized Newtonian fluids at $Re_{\tau } = 180$. J. Non-Newtonian Fluid Mech. 314, 105015.CrossRefGoogle Scholar
Le Clainche, S., Izbassarov, D., Rosti, M., Brandt, L. & Tammisola, O. 2020 Coherent structures in the turbulent channel flow of an elastoviscoplastic fluid. J. Fluid Mech. 888, A5.CrossRefGoogle Scholar
Leonard, B.P. 1995 Order of accuracy of quick and related convection-diffusion schemes. Appl. Math. Model. 19 (11), 640–653.CrossRefGoogle Scholar
Ma, R., Alamé, K. & Mahesh, K. 2021 Direct numerical simulation of turbulent channel flow over random rough surfaces. J. Fluid Mech. 908, A40.CrossRefGoogle Scholar
Madlener, K., Frey, B. & Ciezki, H.K. 2009 Generalized Reynolds number for non-Newtonian fluids. Prog. Propul. Phys. 1, 237–250.CrossRefGoogle Scholar
Menon, E.S. 2014 Transmission Pipeline Calculations and Simulations Manual, Chapter 5 – Fluid Flow in Pipes. Gulf Professional Publishing.Google Scholar
Metzner, A.B. & Reed, J.C. 1955 Flow of non-Newtonian fluids – correlation for the laminar, transition, and turbulent flow regions. AIChE J. 1 (4), 434–440.CrossRefGoogle Scholar
Mitishita, R.S., MacKenzie, J.A., Elfring, G.J. & Frigaard, I.A. 2021 Fully turbulent flows of viscoplastic fluids in a rectangular duct. J. Non-Newtonian Fluid Mech. 293, 104570.CrossRefGoogle Scholar
Mitsoulis, E. & Tsamopoulos, J. 2017 Numerical simulations of complex yield-stress fluid flows. Rheol. Acta 56, 231–258.CrossRefGoogle Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.CrossRefGoogle Scholar
Napoli, E., Armenio, V. & De Marchis, M. 2008 The effect of the slope of irregularly distributed roughness elements on turbulent wall-bounded flows. J. Fluid Mech. 613, 385–394.CrossRefGoogle Scholar
Narayanan, C., Nauer, S., Singh, J.-S., Belt, R., Palermo, T. & Lakehal, D. 2024 Direct numerical simulation of turbulent flow over irregular rough surfaces. Phys. Fluids 36 (6), 065166.CrossRefGoogle Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62 (3), 183–200.CrossRefGoogle Scholar
Ohta, T. & Miyashita, M. 2014 DNS and LES with an extended Smagorinsky model for wall turbulence in non-Newtonian viscous fluids. J. Non-Newtonian Fluid Mech. 206, 29–39.CrossRefGoogle Scholar
Palermo, T. & Tournis, E. 2015 Viscosity prediction of waxy oils: suspension of fractal aggregates (SoFA) model. Ind. Eng. Chem. Res 54, 4526–4534.CrossRefGoogle Scholar
Peixinho, J., Nouar, C., Desaubry, C. & Théron, B. 2005 Laminar transitional and turbulent flow of yield stress fluid in a pipe. J. Non-Newtonian Fluid Mech. 128 (2–3), 172–184.CrossRefGoogle Scholar
Peskin, C.S. 1977 Numerical analysis of blood flow in the heart. J. Comput. Phys. 25 (3), 220–252.CrossRefGoogle Scholar
Pinho, F.T. & Whitelaw, J.H. 1990 Flow of non-Newtonian fluids in a pipe. J. Non-Newtonian Fluid Mech. 34, 129–144.CrossRefGoogle Scholar
Rahgozar, S. & Rival, D.E. 2017 On turbulence decay of a shear-thinning fluid. Phys. Fluids 29 (12), 123101.CrossRefGoogle Scholar
Rubin, S.G. & Khosla, P.K. 1977 Turbulent boundary layers with and without mass injection. Comput. Fluid 5, 241.CrossRefGoogle Scholar
Rudman, M. & Blackburn, H.M. 2006 Direct numerical simulation of turbulent non-Newtonian flow using a spectral element method. Appl. Math. Model. 30 (11), 1229–1248.CrossRefGoogle Scholar
Singh, J., Rudman, M. & Blackburn, H.M. 2017 The influence of shear-dependent rheology on turbulent pipe flow. J. Fluid Mech. 822, 848.CrossRefGoogle Scholar
Singh, J., Rudman, M. & Blackburn, H.M. 2018 Reynolds number effects in pipe flow turbulence of generalized Newtonian fluids. Phys. Rev. Fluids 3, 094607.CrossRefGoogle Scholar
Singh, J., Rudman, M., Blackburn, H.M., Chryss, A., Pullum, L. & Graham, L.J.W. 2016 The importance of rheology characterization in predicting turbulent pipe flow of generalized Newtonian fluids. J. Non-Newtonian Fluid Mech. 100 (232), 11–21.CrossRefGoogle Scholar
Van Doormaal, J.P. & Raithby, G.D. 1984 Enhancements of the simple method for predicting incompressible fluid flows. Numer. Heat Transfer 7 (2), 147–163.CrossRefGoogle Scholar
Wu, S., Christensen, K.T. & Pantano, C. 2019 Modelling smooth-and transitionally rough-wall turbulent channel flow by leveraging inner–outer interactions and principal component analysis. J. Fluid Mech. 863, 407–453.CrossRefGoogle Scholar
Yuan, J. & Aghaei Jouybari, M. 2018 Topographical effects of roughness on turbulence statistics in roughness sublayer. Phys. Rev. Fluids 3 (11), 114603.CrossRefGoogle Scholar
Yuan, J. & Piomelli, U. 2014 Roughness effects on the Reynolds stress budgets in near-wall turbulence. J. Fluid Mech. 760, R1.CrossRefGoogle Scholar
Zheng, S., Saidoun, M., Palermo, T., Mateen, K. & Fogler, H.S. 2017 Wax deposition modeling with considerations of non-Newtonian characteristics: application on field-scale pipeline. Energy Fuels 31 (5), 5011–5023.CrossRefGoogle Scholar