Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T17:53:02.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flow of finite-size spherical particles in channels with viscous hyper-elastic walls

Published online by Cambridge University Press:  24 June 2019

M. N. Ardekani Open the ORCID record for M. N. Ardekani [Opens in a new window] ,
M. E. Rosti Open the ORCID record for M. E. Rosti [Opens in a new window]  and
L. Brandt Open the ORCID record for L. Brandt [Opens in a new window]
M. N. Ardekani*
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
M. E. Rosti
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
L. Brandt
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study single-phase and particle-laden turbulent channel flows bounded by two incompressible hyper-elastic walls with different deformability at bulk Reynolds number 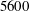$5600$. The solid volume fraction of finite-size neutrally buoyant rigid spherical particles considered is 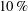$10\,\%$. The elastic walls are assumed to be of a neo-Hookean material. A fully Eulerian formulation is employed to model the elastic walls together with a direct-forcing immersed boundary method for the coupling between the fluid and the particles. The data show a significant drag increase and the enhancement of the turbulence activity with growing wall elasticity for both the single-phase and particle-laden flows when compared with the single-phase flow over rigid walls. Drag reduction and turbulence attenuation is obtained, on the other hand, with highly elastic walls when comparing the particle-laden flow with the single-phase flow for the same wall properties; the opposite effect, drag increase, is observed upon adding particles to the flow over less elastic walls. This is explained by investigating the near-wall turbulence, where the strong asymmetry in the magnitude of the wall-normal velocity fluctuations (favouring positive 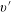$v^{\prime }$), is found to push the particles towards the channel centre. The particle layer close to the wall contributes to turbulence production by increasing the wall-normal velocity fluctuations, so that in the absence of this layer, smaller wall deformations and in turn turbulence attenuation is observed. For a moderate wall elasticity, we increase the particle volume fraction up to $20\,\%$ and find that particle migration away from the wall is the cause of turbulence attenuation with respect to the flow over rigid walls. However, for this higher volume fractions, the particle induced stress compensates for the decreasing Reynolds shear stress, resulting in a higher overall drag for the case with elastic walls. The effect of the wall elasticity on the overall drag reduces significantly with increasing particle volume fraction.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 410 - 440
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Krogstad, P.-Å. 2001 Turbulence structure in boundary layers over different types of surface roughness. Fluid Dyn. Res. 28 (2), 139.10.1016/S0169-5983(00)00025-3Google Scholar
Ardekani, M. N., Al Asmar, L., Picano, F. & Brandt, L. 2018 Numerical study of heat transfer in laminar and turbulent pipe flow with finite-size spherical particles. Intl J. Heat Fluid Flow 71, 189–199.10.1016/j.ijheatfluidflow.2018.04.002Google Scholar
Ardekani, M. N. & Brandt, L. 2019 Turbulence modulation in channel flow of finite-size spheroidal particles. J. Fluid Mech. 859, 887–901.10.1017/jfm.2018.854Google Scholar
Ardekani, M. N., Costa, P., Breugem, W. P. & Brandt, L. 2016 Numerical study of the sedimentation of spheroidal particles. Intl J. Multiphase Flow 87, 16–34.10.1016/j.ijmultiphaseflow.2016.08.005Google Scholar
Ardekani, M. N., Costa, P., Breugem, W. P., Picano, F. & Brandt, L. 2017 Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.10.1017/jfm.2017.68Google Scholar
Beavers, G. S., Sparrow, E. M. & Magnuson, R. A. 1970 Experiments on coupled parallel flows in a channel and a bounding porous medium. Trans. ASME J. Basic Engng 92 (4), 843–848.10.1115/1.3425155Google Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.10.1017/S0022112003005019Google Scholar
Bolotnov, I. A., Jansen, K. E., Drew, D. A., Oberai, A. A., Lahey, R. T. Jr & Podowski, M. Z. 2011 Detached direct numerical simulations of turbulent two-phase bubbly channel flow. Intl J. Multiphase Flow 37 (6), 647–659.10.1016/j.ijmultiphaseflow.2011.03.002Google Scholar
Bonet, J. & Wood, R. D. 1997 Nonlinear Continuum Mechanics for Finite Element Analysis. Cambridge university press.Google Scholar
Brandt, L. 2014 The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur. J. Mech. (B/Fluids) 47, 80–96.10.1016/j.euromechflu.2014.03.005Google Scholar
Breugem, W-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.10.1016/j.jcp.2012.02.026Google Scholar
Breugem, W.-P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.10.1017/S0022112006000887Google Scholar
Breugem, W. P., Van Dijk, V. & Delfos, R. 2014 Flows through real porous media: X-ray computed tomography, experiments, and numerical simulations. Trans. ASME J. Fluids Engng 136 (4), 040902.10.1115/1.4025311Google Scholar
Cabal, A., Szumbarski, J. & Floryan, J. M. 2002 Stability of flow in a wavy channel. J. Fluid Mech. 457, 191–212.10.1017/S0022112001007546Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Costa, P., Boersma, B. J., Westerweel, J. & Breugem, W.-P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.10.1103/PhysRevE.92.053012Google Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2016 Universal scaling laws for dense particle suspensions in turbulent wall-bounded flows. Phys. Rev. Lett. 117 (13), 134501.10.1103/PhysRevLett.117.134501Google Scholar
Costa, P., Picano, F., Brandt, L. & Breugem, W.-P. 2018 Effects of the finite particle size in turbulent wall-bounded flows of dense suspensions. J. Fluid Mech. 843, 450–478.10.1017/jfm.2018.117Google Scholar
De Vita, F., Rosti, M. E., Caserta, S. & Brandt, L.2019 Numerical simulations of vorticity banding of emulsions in shear flows. arXiv:1902.05448.10.1039/C9SM01898KGoogle Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.10.1017/CBO9780511616938Google Scholar
Eshghinejadfard, A., Hosseini, S. A. & Thévenin, D. 2017 Fully-resolved prolate spheroids in turbulent channel flows: A lattice Boltzmann study. AIP Advances 7 (9), 095007.10.1063/1.5002528Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.10.1146/annurev.fluid.32.1.519Google Scholar
Freund, J. B. 2014 Numerical simulation of flowing blood cells. Annu. Rev. Fluid Mech. 46, 67–95.10.1146/annurev-fluid-010313-141349Google Scholar
Gualtieri, P., Battista, F. & Casciola, C. M. 2017 Turbulence modulation in heavy-loaded suspensions of tiny particles. Phys. Rev. Fluids 2 (3), 034304.10.1103/PhysRevFluids.2.034304Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics, vol. 45. Cambridge University Press.10.1017/CBO9780511894671Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.10.1016/0021-9991(81)90145-5Google Scholar
Izbassarov, D., Rosti, M. E., Ardekani, M. N., Sarabian, M., Hormozi, S., Brandt, L. & Tammisola, O. 2018 Computational modeling of multiphase viscoelastic and elasto-viscoplastic flows. Intl J. Numer. Meth. Fluids 88, 521–543.10.1002/fld.4678Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.10.1017/S0022112081002279Google Scholar
Jeffrey, D. J. 1982 Low-Reynolds-number flow between converging spheres. Mathematika 29, 58–66.10.1112/S002557930001216XGoogle Scholar
Jiménez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.10.1017/S0022112001004888Google Scholar
Kajishima, T., Takiguchi, S., Hamasaki, H. & Miyake, Y. 2001 Turbulence structure of particle-laden flow in a vertical plane channel due to vortex shedding. JSME Intl J. 44 (4), 526–535.10.1299/jsmeb.44.526Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.10.1017/S0022112087000892Google Scholar
Krindel, P. & Silberberg, A. 1979 Flow through gel-walled tubes. J. Colloid Interface Sci. 71 (1), 39–50.10.1016/0021-9797(79)90219-4Google Scholar
Krogstadt, P. & Antonia, R. A. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27 (5), 450–460.10.1007/s003480050370Google Scholar
Kumaran, V. 1995 Stability of the flow of a fluid through a flexible tube at high Reynolds number. J. Fluid Mech. 302, 117–139.10.1017/S0022112095004034Google Scholar
Kumaran, V. 1998a Stability of the flow of a fluid through a flexible tube at intermediate Reynolds number. J. Fluid Mech. 357, 123–140.10.1017/S0022112097008033Google Scholar
Kumaran, V. 1998b Stability of wall modes in a flexible tube. J. Fluid Mech. 362, 1–15.10.1017/S002211209700832XGoogle Scholar
Kumaran, V. & Muralikrishnan, R. 2000 Spontaneous growth of fluctuations in the viscous flow of a fluid past a soft interface. Phys. Rev. Lett. 84 (15), 3310.10.1103/PhysRevLett.84.3310Google Scholar
Lahav, J., Eliezer, N. & Silberberg, A. 1973 Gel-walled cylindrical channels as models for the microcirculation: dynamics of flow. Biorheology 10 (4), 595–604.10.3233/BIR-1973-10413Google Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2014 Laminar, turbulent, and inertial shear-thickening regimes in channel flow of neutrally buoyant particle suspensions. Phys. Rev. Lett. 113 (25), 254502.10.1103/PhysRevLett.113.254502Google Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2016 Channel flow of rigid sphere suspensions: particle dynamics in the inertial regime. Intl J. Multiphase Flow 78, 12–24.10.1016/j.ijmultiphaseflow.2015.09.008Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.10.1017/S0022112090000532Google Scholar
Leonardi, S., Orlandi, P., Djenidi, L. & Antonia, R. A. 2004 Structure of turbulent channel flow with square bars on one wall. Intl J. Heat Fluid Flow 25 (3), 384–392.10.1016/j.ijheatfluidflow.2004.02.022Google Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.10.1017/S0022112003005500Google Scholar
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar-turbulent transition regime. Phys. Fluids 25 (12), 123304.10.1063/1.4848856Google Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Lundell, F., Söderberg, L. D. & Alfredsson, P. H. 2011 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.10.1146/annurev-fluid-122109-160700Google Scholar
Luo, H. & Bewley, T. R. 2003 Design, modeling, and optimization of compliant tensegrity fabrics for the reduction of turbulent skin friction. In Smart Structures and Materials 2003: Modeling, Signal Processing, and Control, vol. 5049, pp. 460–471. International Society for Optics and Photonics.Google Scholar
Luo, H. & Bewley, T. R. 2005 Accurate simulation of near-wall turbulence over a compliant tensegrity fabric. In Smart Structures and Materials 2005: Modeling, Signal Processing, and Control, vol. 5757, pp. 184–198. International Society for Optics and Photonics.10.1117/12.600582Google Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90 (1), 014501.10.1103/PhysRevLett.90.014501Google Scholar
McKinney, W. & DeLaurier, J. 1981 Wingmill: an oscillating-wing windmill. J. Energy 5 (2), 109–115.10.2514/3.62510Google Scholar
Mehta, A. J. 2014 An Introduction to Hydraulics of Fine Sediment Transport. World Scientific.Google Scholar
Min, T., Yoo, J. Y. & Choi, H. 2001 Effect of spatial discretization schemes on numerical solutions of viscoelastic fluid flows. J. Non-Newtonian Fluid Mech. 100 (1-3), 27–47.Google Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12 (3), 033040.10.1088/1367-2630/12/3/033040Google Scholar
Nikuradse, J.1933 Stromungsgcsetzc in rauhen Rohren, Forschungshefte, 361, VDI. NACA Tech Mem 1292.Google Scholar
Nikuradse, J. 1950 Laws of flow in rough pipes. National Advisory Committee for Aeronautics Washington.Google Scholar
Orlandi, P. & Leonardi, S. 2008 Direct numerical simulation of three-dimensional turbulent rough channels: parameterization and flow physics. J. Fluid Mech. 606, 399–415.10.1017/S0022112008001985Google Scholar
Pan, Y. & Banerjee, S. 1996 Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 8 (10), 2733–2755.10.1063/1.869059Google Scholar
Perot, B. & Moin, P. 1995a Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.10.1017/S0022112095001935Google Scholar
Perot, B. & Moin, P. 1995b Shear-free turbulent boundary layers. Part 2. New concepts for Reynolds stress transport equation modelling of inhomogeneous flows. J. Fluid Mech. 295, 229–245.10.1017/S0022112095001947Google Scholar
Picano, F., Breugem, W. P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.10.1017/jfm.2014.704Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.10.1017/CBO9780511840531Google Scholar
Quintard, M. & Whitaker, S. 1994 Transport in ordered and disordered porous media II: Generalized volume averaging. Transp. Porous Med. 14 (2), 179–206.10.1007/BF00615200Google Scholar
Rallabandi, B., Saintyves, B., Jules, T., Salez, T., Schönecker, C., Mahadevan, L. & Stone, H. A. 2017 Rotation of an immersed cylinder sliding near a thin elastic coating. Phys. Rev. Fluids 2 (7), 074102.10.1103/PhysRevFluids.2.074102Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Roma, A. M., Peskin, C. S. & Berger, M. J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.10.1006/jcph.1999.6293Google Scholar
Rosti, M. E. & Brandt, L. 2017 Numerical simulation of turbulent channel flow over a viscous hyper-elastic wall. J. Fluid Mech. 830, 708–735.10.1017/jfm.2017.617Google Scholar
Rosti, M. E. & Brandt, L. 2018 Suspensions of deformable particles in a Couette flow. J. Non-Newtonian Fluid Mech. 262 (C), 3–11.10.1016/j.jnnfm.2018.01.008Google Scholar
Rosti, M. E., Brandt, L. & Mitra, D. 2018a Rheology of suspensions of viscoelastic spheres: Deformability as an effective volume fraction. Phys. Rev. Fluids 3 (1), 012301(R).10.1103/PhysRevFluids.3.012301Google Scholar
Rosti, M. E., Brandt, L. & Pinelli, A. 2018b Turbulent channel flow over an anisotropic porous wall – drag increase and reduction. J. Fluid Mech. 842, 381–394.Google Scholar
Rosti, M. E., Cortelezzi, L. & Quadrio, M. 2015 Direct numerical simulation of turbulent channel flow over porous walls. J. Fluid Mech. 784, 396–442.Google Scholar
Saintyves, B., Jules, T., Salez, T. & Mahadevan, L. 2016 Self-sustained lift and low friction via soft lubrication. Proc. Natl Acad. Sci. USA 113 (21), 5847–5849.10.1073/pnas.1525462113Google Scholar
Salez, T. & Mahadevan, L. 2015 Elastohydrodynamics of a sliding, spinning and sedimenting cylinder near a soft wall. J. Fluid Mech. 779, 181–196.Google Scholar
Samanta, A., Vinuesa, R., Lashgari, I., Schlatter, P. & Brandt, L. 2015 Enhanced secondary motion of the turbulent flow through a porous square duct. J. Fluid Mech. 784, 681–693.Google Scholar
Shankar, V. & Kumaran, V. 1999 Stability of non-parabolic flow in a flexible tube. J. Fluid Mech. 395, 211–236.10.1017/S0022112099005960Google Scholar
Shao, X., Wu, T. & Yu, Z. 2012 Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low reynolds number. J. Fluid Mech. 693, 319–344.10.1017/jfm.2011.533Google Scholar
Skotheim, J. M. & Mahadevan, L. 2004 Soft lubrication. Phys. Rev. Lett. 92 (24), 245509.Google Scholar
Srivatsan, L. & Kumaran, V. 1997 Flow induced instability of the interface between a fluid and a gel. J. Phys. II 7 (6), 947–963.Google Scholar
Suga, K., Matsumura, Y., Ashitaka, Y., Tominaga, S. & Kaneda, M. 2010 Effects of wall permeability on turbulence. Intl J. Heat Fluid Flow 31 (6), 974–984.10.1016/j.ijheatfluidflow.2010.02.023Google Scholar
Sugiyama, K., Ii, S., Takeuchi, S., Takagi, S. & Matsumoto, Y. 2011 A full Eulerian finite difference approach for solving fluid–structure coupling problems. J. Comput. Phys. 230 (3), 596–627.Google Scholar
Tanaka, M. & Teramoto, D. 2015 Modulation of homogeneous shear turbulence laden with finite-size particles. J. Turbul. 16 (10), 979–1010.10.1080/14685248.2015.1050105Google Scholar
Tilton, N. & Cortelezzi, L. 2006 The destabilizing effects of wall permeability in channel flows: A linear stability analysis. Phys. Fluids 18 (5), 051702.10.1063/1.2202649Google Scholar
Tryggvason, G., Sussman, M. & Hussaini, M. Y. 2007 Immersed boundary methods for fluid interfaces. In Computational Methods for Multiphase Flow, chap. 3. Cambridge University Press.Google Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for simulation of particulate flow. J. Comput. Phys. 209 (2), 448–476.Google Scholar
Vreman, A. W. 2015 Turbulence attenuation in particle-laden flow in smooth and rough channels. J. Fluid Mech. 773, 103–136.10.1017/jfm.2015.208Google Scholar
Wang, G., Abbas, M. & Climent, E. 2018 Modulation of the regeneration cycle by neutrally buoyant finite-size particles. J. Fluid Mech. 852, 257–282.10.1017/jfm.2018.513Google Scholar
Yu, Z., Wu, T., Shao, X. & Lin, J. 2013 Numerical studies of the effects of large neutrally buoyant particles on the flow instability and transition to turbulence in pipe flow. Phys. Fluids 25 (4), 043305.10.1063/1.4802040Google Scholar
Zhang, Q. & Prosperetti, A. 2010 Physics-based analysis of the hydrodynamic stress in a fluid-particle system. Phys. Fluids 22 (3), 033306.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar
Zhu, W., Van Hout, R. & Katz, J. 2007 PIV measurements in the atmospheric boundary layer within and above a mature corn canopy. Part II: Quadrant-hole analysis. J. Atmos. Sci. 64 (8), 2825–2838.Google Scholar