Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bottaro, Alessandro
2019.
Flow over natural or engineered surfaces: an adjoint homogenization perspective.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
Gómez-de-Segura, G.
and
García-Mayoral, R.
2019.
Turbulent drag reduction by anisotropic permeable substrates – analysis and direct numerical simulations.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
124.
Le Clainche, Soledad
Rosti, Marco
and
Brandt, Luca
2020.
Flow structures and shear-stress predictions in the turbulent channel flow over an anisotropic porous wall.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012016.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
Fan, Yitong
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012010.
Nishiyama, Yudai
Kuwata, Yusuke
and
Suga, Kazuhiko
2020.
Direct numerical simulation of turbulent heat transfer over fully resolved anisotropic porous structures.
International Journal of Heat and Fluid Flow,
Vol. 81,
Issue. ,
p.
108515.
Sharma, Akshath
and
García-Mayoral, Ricardo
2020.
Turbulent flows over dense filament canopies.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Chavarin, Andrew
Efstathiou, Christoph
Vijay, Shilpa
and
Luhar, Mitul
2020.
Resolvent-based design and experimental testing of porous materials for passive turbulence control.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108722.
Corrochano, Adrián
Xavier, Donnatella
Schlatter, Philipp
Vinuesa, Ricardo
and
Le Clainche, Soledad
2020.
Flow Structures on a Planar Food and Drug Administration (FDA) Nozzle at Low and Intermediate Reynolds Number.
Fluids,
Vol. 6,
Issue. 1,
p.
4.
Gómez-de-Segura, Garazi
and
García-Mayoral, Ricardo
2020.
Imposing virtual origins on the velocity components in direct numerical simulations.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108675.
Li, Qingxiang
Pan, Ming
Zhou, Quan
and
Dong, Yuhong
2020.
Turbulent drag modification in open channel flow over an anisotropic porous wall.
Physics of Fluids,
Vol. 32,
Issue. 1,
Chavarin, A.
Gómez-de-Segura, G.
García-Mayoral, R.
and
Luhar, M.
2021.
Resolvent-based predictions for turbulent flow over anisotropic permeable substrates.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Cheng, Shyuan
Elgendi, Mahmoud
Lu, Fanghan
and
Chamorro, Leonardo P.
2021.
On the Wind Turbine Wake and Forest Terrain Interaction.
Energies,
Vol. 14,
Issue. 21,
p.
7204.
2021.
Higher Order Dynamic Mode Decomposition and Its Applications.
p.
291.
Wang, Wenkang
Chu, Xu
Lozano-Durán, Adrián
Helmig, Rainer
and
Weigand, Bernhard
2021.
Information transfer between turbulent boundary layers and porous media.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Endrikat, S.
Modesti, D.
García-Mayoral, R.
Hutchins, N.
and
Chung, D.
2021.
Influence of riblet shapes on the occurrence of Kelvin–Helmholtz rollers.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Ledda, Pier Giuseppe
Boujo, E.
Camarri, S.
Gallaire, F.
and
Zampogna, G.A.
2021.
Homogenization-based design of microstructured membranes: wake flows past permeable shells.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Ibrahim, Joseph I.
Gómez-de-Segura, Garazi
Chung, Daniel
and
García-Mayoral, Ricardo
2021.
The smooth-wall-like behaviour of turbulence over drag-altering surfaces: a unifying virtual-origin framework.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Vega, José M.
and
Le Clainche, Soledad
2021.
Higher Order Dynamic Mode Decomposition and Its Applications.
p.
189.
Chu, Xu
Wang, Wenkang
Yang, Guang
Terzis, Alexandros
Helmig, Rainer
and
Weigand, Bernhard
2021.
Transport of Turbulence Across Permeable Interface in a Turbulent Channel Flow: Interface-Resolved Direct Numerical Simulation.
Transport in Porous Media,
Vol. 136,
Issue. 1,
p.
165.
Martín, Juan A.
Corrochano, Adrián
Sierra, Javier
Fabre, David
and
Le Clainche, Soledad
2021.
15th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2020).
Vol. 1268,
Issue. ,
p.
451.
 ${\approx}$20–25 % at a friction Reynolds number
${\approx}$20–25 % at a friction Reynolds number 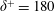 $\unicode[STIX]{x1D6FF}^{+}=180$.
$\unicode[STIX]{x1D6FF}^{+}=180$.