Article contents
Turbulent buoyant convection from a maintained source of buoyancy in a narrow vertical tank
Published online by Cambridge University Press: 10 May 2012
Abstract
We describe new experiments to examine the buoyancy-induced mixing which results from the injection of a small constant volume flux of fluid of density 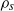 at the top of a long narrow vertical tank with square cross-section which is filled with fluid of density
at the top of a long narrow vertical tank with square cross-section which is filled with fluid of density 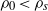 . The injected fluid vigorously mixes with the less dense fluid which initially occupies the tank, such that a dense mixed region of turbulent fluid propagates downwards during the initial mixing phase of the experiment. For an ideal source of constant buoyancy flux
. The injected fluid vigorously mixes with the less dense fluid which initially occupies the tank, such that a dense mixed region of turbulent fluid propagates downwards during the initial mixing phase of the experiment. For an ideal source of constant buoyancy flux 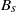 , we show that the height of the mixed region grows as
, we show that the height of the mixed region grows as 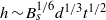 and that the horizontally averaged reduced gravity
and that the horizontally averaged reduced gravity 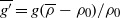 at the top of tank increases as
at the top of tank increases as 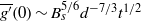 , where
, where 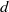 is the width of the tank. Once the mixed region reaches the bottom of the tank, the turbulent mixing continues in an intermediate mixing phase, and we demonstrate that the reduced gravity at each height increases approximately linearly with time. This suggests that the buoyancy flux is uniformly distributed over the full height of the tank. The overall density gradient between the top and bottom of the mixed region is hence time-independent for both the mixing phases before and after the mixed region has reached the bottom of the tank. Our results are consistent with previous models developed for the mixing of an unstable density gradient in a confined geometry, based on Prandtl’s mixing length theory, which suggest that the turbulent diffusion coefficient and the magnitude of the local turbulent flux are given by the nonlinear relations
is the width of the tank. Once the mixed region reaches the bottom of the tank, the turbulent mixing continues in an intermediate mixing phase, and we demonstrate that the reduced gravity at each height increases approximately linearly with time. This suggests that the buoyancy flux is uniformly distributed over the full height of the tank. The overall density gradient between the top and bottom of the mixed region is hence time-independent for both the mixing phases before and after the mixed region has reached the bottom of the tank. Our results are consistent with previous models developed for the mixing of an unstable density gradient in a confined geometry, based on Prandtl’s mixing length theory, which suggest that the turbulent diffusion coefficient and the magnitude of the local turbulent flux are given by the nonlinear relations 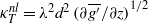 and
and 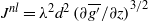 , respectively. The
, respectively. The 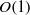 constant
constant 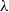 relates the width of the tank to the characteristic mixing length of the turbulent eddies. Since the mixed region is characterized by a time-independent overall density gradient, we also tested the predictions based on a linear model in which the turbulent diffusion coefficient is approximated by a constant
relates the width of the tank to the characteristic mixing length of the turbulent eddies. Since the mixed region is characterized by a time-independent overall density gradient, we also tested the predictions based on a linear model in which the turbulent diffusion coefficient is approximated by a constant 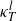 . We solve the corresponding nonlinear and linear turbulent diffusion equations for both mixing phases, and show a good agreement with experimental profiles measured by a dye attenuation technique, in particular for the solutions based on the nonlinear model.
. We solve the corresponding nonlinear and linear turbulent diffusion equations for both mixing phases, and show a good agreement with experimental profiles measured by a dye attenuation technique, in particular for the solutions based on the nonlinear model.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 19
- Cited by


