Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T14:29:21.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent bubbly flow in pipe under gravity and microgravity conditions

Published online by Cambridge University Press:  27 September 2012

Catherine Colin ,
Jean Fabre  and
Arjan Kamp
Catherine Colin
Affiliation:
Institut de Mécanique des Fluides, Institut National Polytechnique de Toulouse, Allée du Prof. Camille Soula, 31400 Toulouse, France
Jean Fabre*
Affiliation:
Institut de Mécanique des Fluides, Institut National Polytechnique de Toulouse, Allée du Prof. Camille Soula, 31400 Toulouse, France
Arjan Kamp
Affiliation:
Centre Scientifique et Technique Jean-Féger, TOTAL, Avenue Larribau, 64018 Pau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

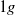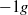Experiments on vertical turbulent flow with millimetric bubbles, under three gravity conditions, upward, downward and microgravity flows (, and 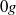), have been performed to understand the influence of gravity upon the flow structure and the phase distribution. The mean and fluctuating phase velocities, shear stress, turbulence production, gas fraction and bubble size have been measured or determined. The results for 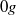flow obtained during parabolic flights are taken as reference for buoyant 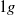and 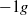flows. Three buoyancy numbers are introduced to understand and quantify the effects of gravity with respect to friction. We show that the kinematic structure of the liquid is similar to single-phase flow for 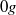flow whereas it deviates in 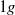and 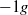buoyant flows. The present results confirm the existence of a two-layer structure for buoyant flows with a nearly homogeneous core and a wall layer similar to the single-phase inertial layer whose thickness seems to result from a friction–gravity balance. The distributions of phase velocity, shear stress and turbulence are discussed in the light of various existing physical models. This leads to a dimensionless correlation that quantifies the wall shear stress increase due to buoyancy. The turbulent dispersion, the lift and the nonlinear effects of added mass are taken into account in a simplified model for the phase distribution. Its analytical solution gives a qualitative description of the gas fraction distribution in the wall layer.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Gas/liquid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 469 - 515
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adoua, R., Legendre, D. & Magnaudet, J. 2009 Reversal of the lift force on an oblate bubble in a weakly viscous linear shear flow. J. Fluid Mech. 628, 23–41.CrossRefGoogle Scholar
2. Antal, S. P., Lahey, R. T. & Flaherty, J. E. 1991 Analysis of phase distribution in fully laminar bubbly two-phase flow. Intl J. Multiphase Flow 17, 635–652.CrossRefGoogle Scholar
3. Chahed, J., Colin, C. & Masbernat, L. 2002 Turbulence and phase distribution in bubbly pipe flow under microgravity condition. Trans. ASME: J. Fluids Engng 124, 951–956.Google Scholar
4. Chahed, J. & Masbernat, L. 1998 Effets de paroi sur la distribution de taux de vide dans les écoulements à bulles. C. R. Acad. Sci. IIb 326, 719–726.Google Scholar
5. Chahed, J., Roig, V. & Masbernat, L. 2003 Eulerian–Eulerian two-fluid model for turbulent gas–liquid bubbly flows. Intl J. Multiphase Flow 29, 23–49.CrossRefGoogle Scholar
6. Clark, N. N. & Turton, R. 1988 Chord length distribution related to bubble size distributions in multiphase flows. Intl J. Multiphase Flow 14, 413–424.CrossRefGoogle Scholar
7. Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
8. Colin, C., Fabre, J. & Dukler, A. E. 1991 Gas liquid flow at microgravity conditions. I. Dispersed bubble and slug flow. Intl J. Multiphase Flow 17, 533–544.CrossRefGoogle Scholar
9. Colin, C., Fabre, J. & McQuillen, J. B. 1996 Bubble and slug flow at microgravity conditions: state of knowledge and open questions. Chem. Engng Commun. 141–142, 155–173.CrossRefGoogle Scholar
10. Colin, C. & Legendre, D. 2001 Bubble distribution in turbulent shear flows: experiments and numerical simulations on single bubbles. In 4th International Conference on Multiphase Flows, New Orleans, USA (ed. Michaelides, S. ). CD Rom Publication.Google Scholar
11. Csanady, G. T. 1964 Turbulent diffusion of heavy particles in the atmosphere. J. Atmos. Sci. 21, 201–208.Google Scholar
12. Deutch, E. & Simonin, O. 1991 Large eddy simulation applied to the modelling of particulate transpot coefficients in turbulent two-phase flows. In 8th Symposium on Turbulent Shear Flow, Technical University of Munich, Germany.Google Scholar
13. Drew, D. & Lahey, R. T. 1982 Phase distribution mechanisms in two-phase flow in a circular pipe. J. Fluid Mech. 117, 91–106.CrossRefGoogle Scholar
14. Duineveld, P. 1994. Bouncing and coalescence of two bubbles in water. PhD thesis, University, Twente, Netherland.CrossRefGoogle Scholar
15. Ellingsen, K. & Risso, F. 2001 On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity. J. Fluid Mech. 440, 235–268.CrossRefGoogle Scholar
16. Eppinger, K. 1995 Etude du mouvement des bulles dans une turbulence homogène isotrope. Thesis, INP, Toulouse, France.Google Scholar
17. Fabre, J., Masbernat, L. & Suzanne, C. 1983 Some remarks on the constitutive equations of stratified gas–liquid flow. In Multiphase Flow and Heat Transfer III (ed. Veziroglu, T. N. & Bergles, A. E. ). Fundamental , vol. A. pp. 41–57. Elsevier.Google Scholar
18. Farar, B., Samways, A. L. & Bruun, H. H. 1995 A computer based technique for two-phase flow measurements. Meas. Sci. Technol. 6, 1528–1537.CrossRefGoogle Scholar
19. Fujiwara, A., Minato, D. & Hishida, K. 2004 Effect of bubble diameter on modification of turbulence in an upward pipe flow. Intl J. Heat Fluid Flow 25, 481–488.CrossRefGoogle Scholar
20. Garnier, C., Lance, M. & Marié, J.-L. 2001 Measurement of local flow characteristics in buoyancy-driven bubbly flow at high void fraction. In 4th International Conference on Multiphase Flow, New Orleans, USA (ed. Michaelides, S. ). CD Rom Publication.Google Scholar
21. Grossetête, C. 1995 Experimental investigation and preliminary numerical simulation of void development in a vertical cylindrical pipe. In 2nd International Conference on Multiphase Flow (ed. A. Serizawa, T. Fukano & J. Bataille), Kyoto, Japan, Elsevier.CrossRefGoogle Scholar
22. Hasan, Y. A., Schmidl, W. & Ortiz-Villafuerte, J. 1998 Investigation of the three-dimensional two-phase flow structure in a bubbly pipe flow. Meas. Sci. Technol. 9, 309–326.CrossRefGoogle Scholar
23. Hazaku, T., Takamasa, T. & Hibiki, T. 2012 Characteristics of developing vertical bubbly flow under normal and microgravity conditions. Intl J. Multiphase Flow 38, 53–66.CrossRefGoogle Scholar
24. Herringe, R. A. & Davis, M. R. 1976 Structural development of gas–liquid mixture flows. J. Fluid Mech. 73, 97–123.CrossRefGoogle Scholar
25. Hibiki, T., Goda, H., Kim, S., Ishii, M. & Uhle, J. 2004 Structure of vertical downward bubbly flow. Intl J. Heat Mass Transfer 47, 1847–1862.CrossRefGoogle Scholar
26. Hinze, J. O. 1959 Turbulence. McGraw-Hill.Google Scholar
27. Hosokawa, S., Suzuki, T. & Tomiyama, A. 2010 Effects of bubbles on turbulence properties in a duct flow. Multiphase Sci. Technol. 22, 211–232.CrossRefGoogle Scholar
28. Hosokawa, S. & Tomiyama, A. 2004 Turbulence modification in gas–liquid and solid–liquid dispersed two-phase pipe flows. Intl J. Heat Fluid Flow 25, 489–498.CrossRefGoogle Scholar
29. Hosokawa, S. & Tomiyama, A. 2009a Application of photobleaching molecular tagging velocimetry to turbulent bubbly flow in a square duct. Exp. Fluids 47, 745–754.CrossRefGoogle Scholar
30. Hosokawa, S. & Tomiyama, A. 2009b Multi-fluid simulation of turbulent bubbly pipe flows. Chem. Engng Sci. 64, 5308–5318.CrossRefGoogle Scholar
31. Kamp, A. 1996 Ecoulements turbulents à bulles dans une conduite en micropesanteur. Thesis, INP, Toulouse, France.Google Scholar
32. Kamp, A., Colin, C., Chesters, A. K. & Fabre, J. 2001 Bubble coalescence in turbulent flow: a mechanistic model for turbulence induced coalescence applied to microgravity bubbly pipe flow. Intl J. Multiphase Flow 27 (8), 1363–1396.CrossRefGoogle Scholar
33. Kashinsky, O. N. & Randin, V. V. 1999 Downward bubbly gas–liquid flow in a vertical pipe. Intl J. Multiphase Flow 25, 109–138.CrossRefGoogle Scholar
34. Lahey, R. T. & Bonetto, F. 1994 Analysis of phase distribution phenomena in microgravity environments. In 2nd Microgravity Fluid Physics Conference, Cleveland, Ohio, USA, pp. 193–201. NASA.Google Scholar
35. Lamb, H. 1932 Hydrodynamics. Dover.Google Scholar
36. Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 225, 95–118.CrossRefGoogle Scholar
37. Lance, M. & Lopez de Bertodano, M. 1994 Phase distribution phenomena and wall effects in bubbly two-phase flows. In Multiphase Science and Technology: Two-phase Flow Fundamentals (ed. Hewitt, G. F., Kim, J. H., Lahey, R. T., Delhaye, J.-M. & Zuber, N. ), vol. 8. pp. 69–123. Begell House.Google Scholar
38. Larue de Tournemine, A. 2001 Etude expérimentale de l’effet du taux de vide en écoulement diphasique à bulles. Thesis, INP, Toulouse, France.Google Scholar
39. Laufer, J. 1954 The structure of turbulence in fully developped pipe flow. NACA Rep. 1174.Google Scholar
40. Legendre, D., Colin, C., Fabre, J. & Magnaudet, J. 1999 Influence of gravity upon the bubble distribution in a turbulent pipe flow: comparison between numerical simulations and experimental data. J. Chim. Phys. 96, 951–957.CrossRefGoogle Scholar
41. Liu, T. J. 1989 Experimental investigation of turbulence structure in two-phase bubbly flow. PhD thesis, Northwest University, Evanston, Illinois.Google Scholar
42. Liu, T. J. 1993 Bubble size and entrance length effects on void development in a vertical channel. Intl J. Multiphase Flow 19, 99–113.CrossRefGoogle Scholar
43. Liu, T. J. 1998 The role of bubble size on liquid turbulent structure in two-phase bubbly flow. In 3rd International Conference on Multiphase Flow Lyon, France (ed. Bataille, J. ). CD Rom Publication.Google Scholar
44. Liu, T. J. & Bankoff, S. G. 1993a Structure of air–water bubbly flow in a vertical pipe-1. Liquid velocity and turbulence measurements. Intl J. Heat Mass Transfer 36, 1049–1060.CrossRefGoogle Scholar
45. Liu, T. J. & Bankoff, S. G. 1993b Structure of air–water bubbly flow in a vertical pipe-2 Void fraction, bubble velocity and bubble size distribution. Intl J. Heat Mass Transfer 36, 1061–1072.CrossRefGoogle Scholar
46. Liu, W. & Clark, N. N. 1995 Relationships between distributions of chord lengths and distributions of bubble sizes including their statistical parameters. Intl J. Multiphase Flow 21, 1073–1089.CrossRefGoogle Scholar
47. Lopez de Bertodano, M., Lahey, R. T. & Jones, O. C. 1994 Phase distribution in bubbly two-phase flow in vertical ducts. Intl J. Multiphase Flow 20, 805–818.CrossRefGoogle Scholar
48. Lucas, D., Krepper, E. & Prasser, H.-M. 2007 Use of models for lift, wall and turbulent dispersion forces acting on bubbles for poly-disperse flows. Chem. Engng Sci. 62, 4146–4157.CrossRefGoogle Scholar
49. Magnaudet, J., Rivero, M. & Fabre, J. 1995 Accelerated flows past a rigid sphere or a spherical bubble. Part 1. Steady straining flow. J. Fluid Mech. 284, 97–135.CrossRefGoogle Scholar
50. Marié, J.-L., Moursali, E. & Tran-Cong, S. 1997 Similarity law and turbulence intensity profiles in a bubbly boundary layer at low void fraction. Intl J. Multiphase Flow 23, 227–247.CrossRefGoogle Scholar
51. Mendelson, H. D. 1967 The prediction of bubble terminal velocities from wave theory. AIChE J. 13, 250–253.CrossRefGoogle Scholar
52. Michiyoshi, I. & Serizawa, A. 1986 Turbulence in two-phase bubble flow. Nucl. Engng Des. 95, 253–267.CrossRefGoogle Scholar
53. Nakoryakov, V. E., Kashinsky, O. N., Burdukov, A. P. & Odnoral, V. P. 1981 Local characteristics of upward gas–liquid flow. Intl J. Multiphase Flow 7, 63–81.CrossRefGoogle Scholar
54. Nakoryakov, V. E., Kashinsky, O. N., Randin, V. V. & Timkin, L. S. 1996 Gas–liquid bubbly flow in vertical pipes. Trans. ASME: J. Fluids Engng 118, 377–382.Google Scholar
55. Powell, M. 1964 An efficient method for finding the minimum of a function with several variable without calculating derivatives. Comput. J. 7, 155–162.CrossRefGoogle Scholar
56. Prasser, H.-M., Krepper, E. & Lucas, D. 2002 Evolution of the two-phase flow in a vertical tube: decomposition of gas fraction profiles according to bubble size classes using wire-mesh sensors. Intl J. Therm. Sci. 41, 17–28.CrossRefGoogle Scholar
57. Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.CrossRefGoogle Scholar
58. Sato, Y. & Yamamoto, K. 1987 Lagrangian measurements of fluid-particle motion in approximately homogeneous turbulence. J. Fluid Mech. 88, 63–72.Google Scholar
59. Schlichting, H. 1968 Boundary-layer Theory. McGraw-Hill.Google Scholar
60. Serizawa, A. & Kataoka, I. 1988 Phase distribution in two-phase flow. In Transient Phenomena in Multiphase Flow (ed. Afghan, N. H. ). pp. 179–225. Hemisphere.Google Scholar
61. Serizawa, A. & Kataoka, I. 1990 Turbulence suppression in bubbly two-phase flow. Nucl. Engng Des. 122, 1–16.CrossRefGoogle Scholar
62. Serizawa, A., Kataoka, I. & Michiyoshi, I. 1975 Turbulence structures of air–water bubbly flow -II. Local properties. Intl J. Multiphase Flow 2, 236–246.Google Scholar
63. Shawkat, M. E., Ching, C. Y. & Shoukri, M. 2008 Bubble and liquid turbulence characteristics of bubbly flow in a large diameter vertical pipe. Intl J. Multiphase Flow 34, 767–785.CrossRefGoogle Scholar
64. Takamasa, T., Iguchi, T., Hazaku, T., Hibiki, T. & Ishii, M. 2003 Interfacial area transport of bubbly flow under microgravity environment. Intl J. Multiphase Flow 29, 291–304.CrossRefGoogle Scholar
65. Tchen, C. M. 1947 Mean value and correlation problems connected with the motion of small particles suspended in a turbulent flow. PhD thesis, Technische Hogeschool, Delft, Netherlands.Google Scholar
66. Theofanous, T. G. & Sullivan, J. 1982 Turbulence in two-phase dispersed flows. J. Fluid Mech. 116, 343–362.CrossRefGoogle Scholar
67. Tomiyama, A., Tamai, H., Zun, I. & Hosokawa, S. 2002 Transverse migration of single bubbles in simple shear flows. Chem. Engng Sci. 57, 1849–1858.CrossRefGoogle Scholar
68. Wang, S. K. 1985 Three-dimensional turbulence structure measurements in air–water two-phase flow. PhD Thesis, Nucl. Eng. Dept., Troy, New York.Google Scholar
69. Wang, S. K., Lee, S. J., Jones, O. C. & Lahey, R. T. 1987 3-D turbulence structure and phase distribution measurements in bubbly two-phase flows. Intl J. Multiphase Flow 13, 327–343.CrossRefGoogle Scholar
70. van der Welle, R. 1985 Void fraction, bubble velocity and bubble size in two-phase flow. Intl J. Multiphase Flow 11, 317–345.CrossRefGoogle Scholar
71. Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulation of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar
72. Zun, I. 1988 Transition from wall void peaking to core void peaking in turbulent bubbly flow. In Transient Phenomena in Multiphase Flow (ed. Afghan, N. H. ). Hemisphere.Google Scholar
73. Zun, I., Kljenak, I., Serizawa, A. & Moze, S. 1993 Space time evolution of non homogeneous bubble distribution in upward flow. Intl J. Multiphase Flow 19, 151–172.CrossRefGoogle Scholar
Supplementary material: File

Colin Supplementary Material

Tables

Download Colin Supplementary Material(File)
File 207.7 KB