Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T03:20:17.048Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence structure in a boundary layer with two-dimensional roughness

Published online by Cambridge University Press:  10 September 2009

R. J. VOLINO ,
M. P. SCHULTZ  and
K. A. FLACK
R. J. VOLINO*
Affiliation:
Mechanical Engineering Department, United States Naval Academy, Annapolis, MD 21402, USA
M. P. SCHULTZ
Affiliation:
Naval Architecture and Ocean Engineering Department, United States Naval Academy, Annapolis, MD 21402, USA
K. A. FLACK
Affiliation:
Mechanical Engineering Department, United States Naval Academy, Annapolis, MD 21402, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulence measurements for a zero pressure gradient boundary layer over a two-dimensional roughness are presented and compared to previous results for a smooth wall and a three-dimensional roughness (Volino, Schultz & Flack, J. Fluid Mech., vol. 592, 2007, p. 263). The present experiments were made on transverse square bars in the fully rough flow regime. The turbulence structure was documented through the fluctuating velocity components, two-point correlations of the fluctuating velocity and swirl strength and linear stochastic estimation conditioned on the swirl and Reynolds shear stress. The two-dimensional bars lead to significant changes in the turbulence in the outer flow. 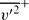Reynolds stresses, particularly and 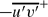, increase, although the mean flow is not as significantly affected. Large-scale turbulent motions originating at the wall lead to increased spatial scales in the outer flow. The dominant feature of the outer flow, however, remains hairpin vortex packets which have similar inclination angles for all wall conditions. The differences between boundary layers over two-dimensional and three-dimensional roughness are attributable to the scales of the motion induced by each type of roughness. This study has shown three-dimensional roughness produces turbulence scales of the order of the roughness height k while the motions generated by two-dimensional roughness may be much larger due to the width of the roughness elements. It is also noted that there are fundamental differences in the response of internal and external flows to strong wall perturbations, with internal flows being less sensitive to roughness effects.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 635 , 25 September 2009 , pp. 75 - 101
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R. J. 1983 Laser velocimetry. In Fluid Mechanics Measurements (ed. Goldstein, R. J.). Hemisphere Publishing.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, Article no. 041301CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Adrian, R. J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure – homogeneous shear-flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
Burattini, P., Leonardi, S., Orlandi, P. & Antonia, R. A. 2008 Comparison between experiments and direct numerical simulations in a channel flow with roughness on one wall. J. Fluid Mech. 600, 403–426.CrossRefGoogle Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.CrossRefGoogle Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban like-roughness. Boundary-Layer Met. 104, 229–259.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of 3-dimensional flow-fields. Phys. Fluids A-Fluid Dyn. 2, 765–777.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Christensen, K. T. & Wu, Y. 2005 Characteristics of vortex organization in the outer layer of wall turbulence. In Proceedings of Fourth International Symposium on Turbulence and Shear Flow Phenomena, Williamsburg, Virginia, vol. 3, pp. 1025–1030.CrossRefGoogle Scholar
Djenidi, L., Antonia, R. A., Amielh, M. & Anselmet, F. 2008 A turbulent boundary layer over a two-dimensional rough wall. Exps. Fluids 44, 37–47.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for boundary layer similarity. Phys. Fluids 19, Article no. 095104.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend's Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17, Article no. 035102.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.CrossRefGoogle Scholar
Furuya, Y., Miyata, M. & Fujita, H. 1976 Turbulent boundary layer and flow resistance on plates roughened by wires. J. Fluids Engng 98, 635–644.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.CrossRefGoogle Scholar
Hutchins, N., Hambleton, W. T. & Marusic, I. 2005 Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Ikeda, T. & Durbin., P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Keirsbulck, L., Labraga, L., Mazouz, A. & Tournier, C. 2002 Surface roughness effects on turbulent boundary layer structures. J. Fluids Engng 124, 127–135.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler., P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
Krogstad, P.-Å. & Antonia, R. A. 1999 Surface roughness effects in turbulent boundary layers. Exps. Fluids 27, 450–460.CrossRefGoogle Scholar
Krogstad, P.-Å., Andersson, H. I., Bakken, O. M. & Ashrafian, A. 2005 An experimental and numerical study of channel flow with rough walls. J. Fluid Mech. 530, 327–352.CrossRefGoogle Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.CrossRefGoogle Scholar
Lee, S. H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number Invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99, Article no. 114504.CrossRefGoogle ScholarPubMed
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. 1969 Rough wall turbulent boundary layer. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary-Layer Theory, 7th ed. McGraw-Hill.Google Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd ed. Cambridge University Press.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.CrossRefGoogle Scholar
Wark, C. E., Naguib, A. M. & Robinson, S. K. 1991 Scaling of spanwise length scales in a turbulent boundary layer. AIAA Paper. 91-0235.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topography. Phys. Fluids 19, Article no. 085108.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar