Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-08T10:04:41.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence structure behind the shock in canonical shock–vortical turbulence interaction

Published online by Cambridge University Press:  01 September 2014

Jaiyoung Ryu  and
Daniel Livescu
Jaiyoung Ryu
Affiliation:
CCS-2, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
Daniel Livescu*
Affiliation:
CCS-2, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction between vortical isotropic turbulence (IT) and a normal shock wave is studied using direct numerical simulation (DNS) and linear interaction analysis (LIA). In previous studies, agreement between the simulation results and the LIA predictions has been limited and, thus, the significance of LIA has been underestimated. 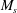In this paper, we present high-resolution simulations which accurately solve all flow scales (including the shock-wave structure) and extensively cover the parameter space (the shock Mach number, $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M_s$, ranges from 1.1 to 2.2 and the Taylor Reynolds number, 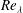${\mathit{Re}}_{\lambda }$, ranges from 10 to 45). The results show, for the first time, that the turbulence quantities from DNS converge to the LIA solutions as the turbulent Mach number, 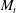$M_t$, becomes small, even at low upstream Reynolds numbers. The classical LIA formulae are extended to compute the complete post-shock flow fields using an IT database. The solutions, consistent with the DNS results, show that the shock wave significantly changes the topology of the turbulent structures, with a symmetrization of the third invariant of the velocity gradient tensor and (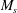$M_s$-mediated) of the probability density function (PDF) of the longitudinal velocity derivatives, and an 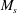$M_s$-dependent increase in the correlation between strain and rotation.

JFM classification

Turbulent Flows: Compressible turbulence Compressible Flows: Shock waves Turbulent Flows: Turbulence simulation
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , R1
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA.

References

Agui, J. H., Briassulis, G. & Andreopoulos, Y. 2005 Studies of interactions of a propagating shock wave with decaying grid turbulence: velocity and vorticity fields. J. Fluid Mech. 524, 143–195.CrossRefGoogle Scholar
Andreopoulos, Y., Agui, J. H. & Briassulis, G. 2000 Shock wave–turbulence interactions. Annu. Rev. Fluid Mech. 32, 309–345.Google Scholar
Barre, S., Alem, D. & Bonnet, J. P. 1996 Experimental study of a normal shock/homogeneous turbulence interaction. AIAA J. 34, 968–974.CrossRefGoogle Scholar
Donzis, D. A. 2012 Amplification factors in shock–turbulence interactions: effect of shock thickness. Phys. Fluids 24, 011705.Google Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound. AIAA J. 35, 740.CrossRefGoogle Scholar
Jamme, S., Cazalbou, J. B., Torres, F. & Chassaing, P. 2002 Direct numerical simulation of the interaction between a shock wave and various types of isotropic turbulence. Flow Turbul. Combust. 68, 277.Google Scholar
Larsson, J., Bermejo-Moreno, I. & Lele, S. K. 2013 Reynolds- and Mach-number effects in canonical shock–turbulence interaction. J. Fluid Mech. 717, 293.Google Scholar
Larsson, J. & Lele, S. K. 2009 Direct numerical simulation of canonical shock/turbulence interaction. Phys. Fluids 21, 126101.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1992 Simulation of spatially evolving turbulence and the applicability of Taylor’s hypothesis in compressible flow. Phys. Fluids 4, 1521.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1993 Direct numerical simulation of isotropic turbulence interacting with a weak shock wave. J. Fluid Mech. 251, 533.CrossRefGoogle Scholar
Lee, S., Lele, S. K. & Moin, P. 1997 Interaction of isotropic turbulence with shock waves: effect of shock strength. J. Fluid Mech. 340, 225.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16.CrossRefGoogle Scholar
Livescu, D., Jaberi, F. A. & Madnia, C. K. 2002 The effects of heat release on the energy exchange in reacting turbulent shear flow. J. Fluid Mech. 450, 35.Google Scholar
Livescu, D., Mohd-Yusof, J., Petersen, M. R. & Grove, J. W.2009 CFDNS: a computer code for direct numerical simulation of turbulent flows. LA-CC-09-100, LANL.Google Scholar
Lund, T. S. & Rogers, M. M. 1994 An improved measure of strain state probability in turbulent flows. Phys. Fluids 6, 1838.Google Scholar
Mahesh, K., Lele, S. K. & Moin, P. 1997 The influence of entropy fluctuations on the interaction of turbulence with a shock wave. J. Fluid Mech. 334, 353.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.CrossRefGoogle Scholar
Moore, F. K.1954 Unsteady oblique interaction of a shock wave with a plane disturbance. NACA TR-1165.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125.Google Scholar
Petersen, M. R. & Livescu, D. 2010 Forcing for statistically stationary compressible isotropic turbulence. Phys. Fluids 22, 116101.Google Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulations of isotropic compressible turbulence: influence of compressibility on dynamics and structures. Phys. Fluids 16, 4386.CrossRefGoogle Scholar
Ribner, H. S.1954 Convection of a pattern of vorticity through a shock wave. NACA TR-1164.Google Scholar
Wang, J., Shi, Y., Wang, L., Xiao, Z., He, X. T. & Chen, S. 2012 Effect of compressibility on the small-scale structures in isotropic turbulence. J. Fluid Mech. 713, 588.Google Scholar