Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-08T10:18:48.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers

Published online by Cambridge University Press:  14 August 2013

B. J. Rosenberg ,
M. Hultmark ,
M. Vallikivi ,
S. C. C. Bailey  and
A. J. Smits
B. J. Rosenberg*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
M. Hultmark
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
M. Vallikivi
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
S. C. C. Bailey
Affiliation:
Department of Mechanical Engineering, University of Kentucky, Lexington, KY 40506, USA
A. J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Well-resolved streamwise velocity spectra are reported for smooth- and rough-wall turbulent pipe flow over a large range of Reynolds numbers. The turbulence structure far from the wall is seen to be unaffected by the roughness, in accordance with Townsend’s Reynolds number similarity hypothesis. Moreover, the energy spectra within the turbulent wall region follow the classical inner and outer scaling behaviour. 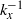While an overlap region between the two scalings and the associated ${ k}_{x}^{- 1} $ law are observed near 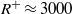${R}^{+ } \approx 3000$, the 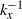${ k}_{x}^{- 1} $ behaviour is obfuscated at higher Reynolds numbers due to the evolving energy content of the large scales (the very-large-scale motions, or VLSMs). We apply a semi-empirical correction (del Álamo & Jiménez, J. Fluid Mech., vol. 640, 2009, pp. 5–26) to the experimental data to estimate how Taylor’s frozen field hypothesis distorts the pseudo-spatial spectra inferred from time-resolved measurements. While the correction tends to suppress the long wavelength peak in the logarithmic layer spectrum, the peak nonetheless appears to be a robust feature of pipe flow at high Reynolds number. The inertial subrange develops around ${R}^{+ } \gt 2000$ where the characteristic 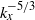${ k}_{x}^{- 5/ 3} $ region is evident, which, for high Reynolds numbers, persists in the wake and logarithmic regions. In the logarithmic region, the streamwise wavelength of the VLSM peak scales with distance from the wall, which is in contrast to boundary layers, where the superstructures have been shown to scale with boundary layer thickness throughout the entire shear layer. Moreover, the similarity in the streamwise wavelength scaling of the large- and very-large-scale motions supports the notion that the two are physically interdependent.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 46 - 63
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, 41–44.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Allen, J. J., Shockling, M. A., Kunkel, G. J. & Smits, A. J. 2007 Turbulent flow in smooth and rough pipes. Phil. Trans. R. Soc. Lond. A 365, 699–714.Google ScholarPubMed
Bailey, S. C. C., Kunkel, G. J., Hultmark, M., Vallikivi, M., Hill, J. P., Meyer, K. A., Tsay, C., Arnold, C. B. & Smits, A. J. 2010 Turbulence measurements using a nanoscale thermal anemometry probe. J. Fluid Mech. 663, 160–179.Google Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365, 665–681.Google Scholar
Guala, M., Hommena, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Hultmark, M. 2012 A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow. J. Fluid Mech. 707, 575–584.Google Scholar
Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2010 Scaling of near-wall turbulence in pipe flow. J. Fluid Mech. 649, 103–113.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, doi:10.1103/PhysRevLett.108.094501.CrossRefGoogle ScholarPubMed
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-walled pipe flow at extreme Reynolds number. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Katul, G. G., Chu, C. R., Parlange, M. B., Albertson, J. D. & Ortenburger, T. A. 1995 Low-wavenumber spectral characteristics of velocity and temperature in the atmospheric surface layer. J. Geophys. Res. 100 (D7) 14243–14255.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kunkel, G. J., Allen, J. J. & Smits, A. J. 2007 Further support for Townsend’s Reynolds number similarity hypothesis in high Reynolds number rough-wall pipe flow. Phys. Fluids 19 (5), 055109.Google Scholar
Langelandsvik, L. I., Kunkel, G. J. & Smits, A. J. 2007 Flow in a commercial steel pipe. J. Fluid Mech. 595, 323–339.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Subminiature hot-wire sensors: development and use. J. Phys. E 20, 323–332.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.Google Scholar
Marusic, I., Uddin, A. K. M. & Perry, A. E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9 (12), 3718–3726.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Monty, J. P. & Chong, M. S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the ${ k}_{1}^{- 1} $ law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. A 365, 807–822.Google Scholar
Perry, A. E. & Abell, C. J. 1977 Asymptotic similarity of turbulence structures in smooth- and rough-walled pipes. J. Fluid Mech. 79, 785–799.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011a High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Smits, A. J., Monty, J., Hultmark, M., Bailey, S. C. C., Hutchins, M. & Marusic, I. 2011b Spatial resolution correction for turbulence measurements. J. Fluid Mech. 676, 41–53.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. 164 (919), 476–490.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vallikivi, M., Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2011 Turbulence measurements in pipe flow using a nano-scale thermal anemometry probe. Exp. Fluids 51 (6), 1521–1527.CrossRefGoogle Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a $30R$ long turbulent pipe flow at ${R}^{+ } = 685$ : large- and very-large-scale motions. J. Fluid Mech. 698, 235–281.Google Scholar
Zagarola, M. V. 1996 Mean-flow scaling of turbulent pipe flow. PhD thesis, Princeton University.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar