Published online by Cambridge University Press: 31 March 2015
Turbulence intensity variations in the outer region of turbulent shear flows are considered, in the context of the diagnostic plot first introduced by Alfredsson et al. (Phys. Fluids, vol. 23, 2011, 041702) and for both (smooth and rough) wall-bounded flows and classical free shear flows. With 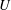 $U$ defined as the mean velocity within the flow,
$U$ defined as the mean velocity within the flow, 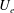 $U_{e}$ as a suitable reference velocity and
$U_{e}$ as a suitable reference velocity and 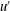 $u^{\prime }$ as the root mean square of the fluctuating velocity, it is demonstrated that, for wall flows, the attached eddy hypothesis yields a closely linear diagnostic plot (
$u^{\prime }$ as the root mean square of the fluctuating velocity, it is demonstrated that, for wall flows, the attached eddy hypothesis yields a closely linear diagnostic plot (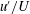 $u^{\prime }/U$ versus
$u^{\prime }/U$ versus 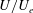 $U/U_{e}$) over a certain Reynolds number range, explaining why the relation seems to work well for both boundary layers and channels despite its lack of any physical basis (Castro et al., J. Fluid Mech., vol. 727, 2013, pp. 119–131). It is shown that mixing layers, jets and wakes also exhibit linear variations of
$U/U_{e}$) over a certain Reynolds number range, explaining why the relation seems to work well for both boundary layers and channels despite its lack of any physical basis (Castro et al., J. Fluid Mech., vol. 727, 2013, pp. 119–131). It is shown that mixing layers, jets and wakes also exhibit linear variations of 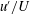 $u^{\prime }/U$ versus
$u^{\prime }/U$ versus 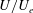 $U/U_{e}$ over much of the flows (starting roughly from where the turbulence production is a maximum), with slopes of these variations determined by the total mean strain rate, characterised by Townsend’s flow constant
$U/U_{e}$ over much of the flows (starting roughly from where the turbulence production is a maximum), with slopes of these variations determined by the total mean strain rate, characterised by Townsend’s flow constant 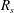 $R_{s}$. The diagnostic plot thus has a wider range of applicability than might have been anticipated.
$R_{s}$. The diagnostic plot thus has a wider range of applicability than might have been anticipated.