Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T16:20:53.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence decay towards the linearly stable regime of Taylor–Couette flow

Published online by Cambridge University Press:  12 May 2014

Rodolfo Ostilla-Mónico ,
Roberto Verzicco ,
Siegfried Grossmann  and
Detlef Lohse
Rodolfo Ostilla-Mónico*
Affiliation:
Physics of Fluids, Mesa+ Institute, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids, Mesa+ Institute, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Meccanica, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Siegfried Grossmann
Affiliation:
Department of Physics, University of Marburg, Renthof 6, D-35032 Marburg, Germany
Detlef Lohse
Affiliation:
Physics of Fluids, Mesa+ Institute, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Taylor–Couette (TC) flow is used to probe the hydrodynamical (HD) stability of astrophysical accretion disks. Experimental data on the subcritical stability of TC flow are in conflict about the existence of turbulence (cf. Ji et al. (Nature, vol. 444, 2006, pp. 343–346) and Paoletti et al. (Astron. Astroph., vol. 547, 2012, A64)), with discrepancies attributed to end-plate effects. In this paper we numerically simulate TC flow with axially periodic boundary conditions to explore the existence of subcritical transitions to turbulence when no end plates are present. We start the simulations with a fully turbulent state in the unstable regime and enter the linearly stable regime by suddenly starting a (stabilizing) outer cylinder rotation. 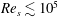The shear Reynolds number of the turbulent initial state is up to $Re_s \lesssim 10^5$ and the radius ratio is 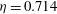$\eta =0.714$. The stabilization causes the system to behave as a damped oscillator and, correspondingly, the turbulence decays. The evolution of the torque and turbulent kinetic energy is analysed and the periodicity and damping of the oscillations are quantified and explained as a function of shear Reynolds number. Though the initially turbulent flow state decays, surprisingly, the system is found to absorb energy during this decay.

JFM classification

Instability: Nonlinear instability Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulent convection
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , R3
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armitage, P. J. 2011 Dynamics of protoplanetary disks. Annu. Rev. Astron. Astrophys. 49, 195–236.CrossRefGoogle Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108 (12), 124501.Google Scholar
Balbus, S. A. & Hawley, J. 1991 A powerful local shear instability in weakly magnetized disks. Astrophys. J. 376, 214–233.Google Scholar
Borrero-Echeverry, D., Schatz, M. F. & Tagg, R. 2010 Transient turbulence in Taylor–Couette flow. Phys. Rev. E 81, 025301.Google Scholar
Brauckmann, H. & Eckhardt, B. 2013 Direct numerical simulations of local and global torque in Taylor–Couette flow up to $Re=30\, 000$ . J. Fluid Mech. 718, 398–427.CrossRefGoogle Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P. Y., Richard, D. & Zahn, J. P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17, 095103.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Edlund, E. M. & Ji, H. 2014 Nonlinear stability of laboratory quasi-Keplerian flows. Phys. Rev. E 89, 021004.Google Scholar
Gallet, B., Doering, C. R. & Spiegel, E. A. 2010 Destabilizing Taylor–Couette flow with suction. Phys. Fluids 22, 034105.Google Scholar
Gammie, C. F. 1996 Layered accretion in T-Tauri disks. Astrophys. J. 457, 355–362.Google Scholar
Grossmann, S. 2000 The onset of shear flow turbulence. Rev. Mod. Phys. 72, 603–618.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
Ji, H. & Balbus, S. A. 2013 Angular momentum transport in astrophysics and in the lab. Phys. Today 66 (8), 27–33.CrossRefGoogle Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444, 343–346.Google Scholar
Klahr, H. H. & Bodenheimer, P. 2003 Turbulence in accretion disks: vorticity generation and angular momentum transport via the global baroclinic instability. Astrophys. J. 508 (2), 869–892.CrossRefGoogle Scholar
Lesur, G. & Longaretti, P. Y. 2005 On the relevance of subcritical hydrodynamic turbulence to accretion disk transport. Astron. Astrophys. 444, 25–44.Google Scholar
Lopez, J. M., Marques, F. & Avila, M. 2013 The Boussinesq approximation in rapidly rotating flows. J. Fluid Mech. 737, 56–77.Google Scholar
Maretzke, S., Hof, B. & Avila, M. 2014 Transient growth in lineraly stable Taylor–Couette flows. J. Fluid Mech. 742, 254–290.Google Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Monico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26, 015114.Google Scholar
Paczynski, B. & Bisnovatyi-Kogan, G. 1981 A model of a thin accretion disk around a black hole. Acta Astron. 31 (3), 283–291.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547, A64.CrossRefGoogle Scholar
Petersen, M. R., Julien, K. & Stewart, G. R. 2007 Baroclinic vorticity production in protoplanetary disks. I. Vortex formation. Astrophys. J. 658, 1236–1251.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
Richard, D.2001 Instabilités hydrodynamiques dans les ecoulements en rotation différentielle. PhD thesis, University of Paris 7.Google Scholar
Rincon, F., Ogilvie, G. I. & Cossu, C. 2008 On self-sustaining processes in Rayleigh-stable rotating plane Couette flows and subcritical transitions to turbulence in accretion disks. Astron. Astrophys. 463, 817–832.Google Scholar
Schartman, E., Ji, H., Burin, M. J. & Goodman, J. 2012 Stability of quasi-Keplerian shear flow in a laboratory experiment. Astron. Astrophys. 543, A94.Google Scholar
Shakura, N. I. & Sunyaev, R. A. 1973 Black holes in binary systems. Observational appearance. Astron. Astrophys. 24, 337–355.Google Scholar
Taylor, G. I. 1917 Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. A 93, 92–113.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscol, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G. W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counter-rotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.CrossRefGoogle Scholar
Velikhov, E. P. 1959 Stability of an ideally conducting liquid flowing between rotating cylinders in a magnetic field. Zh. Eksp. Teor. Fiz. 36.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Withjack, E. M. & Chen, C. F. 1974 An experimental study of Couette instability of stratified fluids. J. Fluid Mech. 66, 725–737.Google Scholar

Ostilla-Mónico supplementary movie

Movie acompanying figure 2.

Download Ostilla-Mónico supplementary movie(Video)
Video 14.4 MB