Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-20T06:04:59.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence and secondary motions in square duct flow

Published online by Cambridge University Press:  14 February 2018

Sergio Pirozzoli Open the ORCID record for Sergio Pirozzoli [Opens in a new window] ,
Davide Modesti ,
Paolo Orlandi  and
Francesco Grasso
Sergio Pirozzoli*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184 Roma, Italy
Davide Modesti
Affiliation:
CNAM-Laboratoire DynFluid, 151 Boulevard de L’Hopital, 75013 Paris, France
Paolo Orlandi
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184 Roma, Italy
Francesco Grasso
Affiliation:
CNAM-Laboratoire DynFluid, 151 Boulevard de L’Hopital, 75013 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

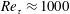We study turbulent flows in pressure-driven ducts with square cross-section through direct numerical simulation in a wide enough range of Reynolds number to reach flow conditions which are representative of fully developed turbulence ($Re_{\unicode[STIX]{x1D70F}}\approx 1000$). Numerical simulations are carried out over very long integration times to get adequate convergence of the flow statistics, and specifically to achieve high-fidelity representation of the secondary motions which arise. The intensity of the latter is found to be on the order of 1 %–2 % of the bulk velocity, and approximately unaffected by Reynolds number variation, at least in the range under scrutiny. The smallness of the mean convection terms in the streamwise vorticity equation points to a simple characterization of the secondary flows, which in the asymptotic high-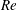$Re$ regime are approximated with good accuracy by eigenfunctions of the Laplace operator, in the core part of the duct. Despite their effect of redistributing the wall shear stress along the duct perimeter, we find that secondary motions do not have a large influence on the bulk flow properties, and the streamwise velocity field can be characterized with good accuracy as resulting from the superposition of four flat walls in isolation. As a consequence, we find that parametrizations based on the hydraulic diameter concept, and modifications thereof, are successful in predicting the duct friction coefficient.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 631 - 655
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Marusic, I. 2012 Coherent structures in flow over hydraulic engineering surfaces. J. Hydraul. Res. 50, 451–464.Google Scholar
Batchelor, G. 1969 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.Google Scholar
Brundrett, E. & Baines, W. D. 1964 The production and diffusion of vorticity in duct flow. J. Fluid Mech. 19 (03), 375–394.Google Scholar
Demuren, A. O. & Rodi, W. 1984 Calculation of turbulence-driven secondary motion in non-circular ducts. J. Fluid Mech. 140, 189–222.Google Scholar
Duan, S., Yovanovich, M. M. & Muzychka, Y. S. 2012 Pressure drop for fully developed turbulent flow in circular and noncircular ducts. Trans. ASME J. Fluids Engng 134 (6), 061201.Google Scholar
Einstein, H. A. & Li, H. 1958 Secondary currents in straight channels. Trans. Am. Geophys. Union 39 (6), 1085–1088.Google Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.Google Scholar
Gessner, F. B. & Jones, J. B. 1965 On some aspects of fully-developed turbulent flow in rectangular channels. J. Fluid Mech. 23 (04), 689–713.Google Scholar
Hoagland, L. C.1960 Fully developed turbulent flow in straight rectangular ducts – secondary flow, its cause and effect on the primary flow. PhD thesis, Department of Mechanical Engineering, Massachusetts Institute of Technology.Google Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.Google Scholar
Jones, O. C. 1976 An improvement in the calculation of turbulent friction in rectangular ducts. Trans. ASME J. Fluids Engng 98, 173–181.CrossRefGoogle Scholar
Khoury, G. K. El, Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Launder, B. E. & Ying, W. M. 1972 Secondary flows in ducts of square cross-section. J. Fluid Mech. 54 (02), 289–295.Google Scholar
Leutheusser, H. J. 1963 Turbulent flow in rectangular ducts. J. Hydraul. Div. ASCE 89 (3), 1–19.Google Scholar
Leutheusser, H. J. 1984 Velocity distribution and skin friction resistance in rectangular ducts. J. Wind Engng Ind. Aerodyn. 16, 315–327.Google Scholar
Mani, M., Babcock, D., Winkler, C. & Spalart, P.2013 Predictions of a supersonic turbulent flow in a square duct. AIAA Paper 2013-0860.CrossRefGoogle Scholar
Marin, O., Vinuesa, R., Obabko, A. V. & Schlatter, P. 2016 Characterization of the secondary flow in hexagonal ducts. Phys. Fluids 28 (12), 125101.CrossRefGoogle Scholar
McKeon, B. J., Li, J., Jiang, W., Morrison, J. F. & Smits, A. J. 2004 Further observations on the mean velocity distribution in fully developed pipe flow. J. Fluid Mech. 501, 135–147.CrossRefGoogle Scholar
Modesti, D. & Pirozzoli, S. 2016 Reynolds and Mach number effects in compressible turbulent channel flow. Intl J. Heat Fluid Flow 59, 33–49.Google Scholar
Modesti, D. & Pirozzoli, S.2017 An efficient semi-implicit solver for direct numerical simulation of compressible flows at all speeds. J. Sci. Comput., doi:10.1007/s10915-017-0534-4.Google Scholar
Nagata, K., Hunt, J. C. R., Sakai, Y. & Wong, H. 2011 Distorted turbulence and secondary flow near right-angled plates. J. Fluid Mech. 668, 446–479.Google Scholar
Nezu, I. 2005 Open-channel flow turbulence and its research prospect in the 21st century. J. Hydraul. Engng 131, 229–246.CrossRefGoogle Scholar
Nikuradse, J. 1930 Turbulente strömung in nicht-kreisförmigen rohren. Ing.-Arch. 1, 306–332.Google Scholar
Oliver, T. A., Malaya, N., Ulerich, R. & Moser, R. D. 2014 Estimating uncertainties in statistics computed from direct numerical simulation. Phys. Fluids 26 (3), 035101.Google Scholar
Orlandi, P. 1990 Vortex dipole rebound from a wall. Phys. Fluids 2, 1429–1436.Google Scholar
Orlandi, P. 2012 Fluid Flow Phenomena: a Numerical Toolkit, vol. 55. Springer Science and Business Media.Google Scholar
Pinelli, A., Uhlmann, M., Sekimoto, A. & Kawahara, G. 2010 Reynolds number dependence of mean flow structure in square duct turbulence. J. Fluid Mech. 644, 107–122.Google Scholar
Pirozzoli, S. 2010 Generalized conservative approximations of split convective derivative operators. J. Comput. Phys. 229 (19), 7180–7190.Google Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds-number effects in numerical boundary layers. Phys. Fluids 25, 021704.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. 1926 Über die ausgebildete turbulenz. In International Congress for Applied Mechanics, Zurich, September 1926.Google Scholar
Prandtl, L.1927 Turbulent flow. NACA TM-435.Google Scholar
Schlichting, H. 1979 Boundary Layer Theory. McGraw-Hill.Google Scholar
Shah, R. K. & London, A. L. 1978 Laminar Flow Forced Convection in Ducts. Academic.Google Scholar
Spalart, P. R., Garbaruk, A. & Stabnikov, A. 2018 On the skin friction due to turbulence in ducts of various shapes. J. Fluid Mech. 838, 369–378.Google Scholar
Speziale, C. G. 1982 On turbulent secondary flows in pipes of noncircular cross-section. Intl J. Engng Sci. 20 (7), 863–872.Google Scholar
Uhlmann, M., Pinelli, A., Kawahara, G. & Sekimoto, A. 2007 Marginally turbulent flow in a square duct. J. Fluid Mech. 588, 153–162.Google Scholar
Vidal, A., Vinuesa, R., Schlatter, P. & Nagib, H. M. 2017 Influence of corner geometry on the secondary flow in turbulent square ducts. Intl J. Heat Fluid Flow 67, 69–78.Google Scholar
Vinuesa, R., Noorani, A., Lozano-Durán, A., Khoury, G. K. El, Schlatter, P., Fischer, P. F. & Nagib, H. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulation. J. Turbul. 15 (10), 677–706.Google Scholar
Vinuesa, R., Prus, C., Schlatter, P. & Nagib, H. M. 2016 Convergence of numerical simulations of turbulent wall-bounded flows and mean cross-flow structure of rectangular ducts. Meccanica 51 (12), 3025–3042.Google Scholar
Wedin, H., Biau, D., Bottaro, A. & Nagata, M. 2008 Coherent flow states in a square duct. Phys. Fluids 20 (9), 094105.Google Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.Google Scholar
Zhang, H., Trias, F. X., Gorobets, A., Tan, Y. & Oliva, A. 2015 Direct numerical simulation of a fully developed turbulent square duct flow up to Re 𝜏 = 1200. Intl J. Heat Fluid Flow 54, 258–267.Google Scholar