Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-09T22:18:20.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence and internal waves in stably-stratified channel flow with temperature-dependent fluid properties

Published online by Cambridge University Press:  07 March 2012

Francesco Zonta ,
Miguel Onorato  and
Alfredo Soldati
Francesco Zonta
Affiliation:
Centro Interdipartimentale di Fluidodinamica e Idraulica and Dipartimento di Energetica e Macchine, Università degli Studi di Udine, via delle Scienze 208, 33100 Udine, Italy Dipartimento di Fisica Generale, Università degli Studi di Torino, via Pietro Giuria 1, 10125 Torino, Italy
Miguel Onorato
Affiliation:
Dipartimento di Fisica Generale, Università degli Studi di Torino, via Pietro Giuria 1, 10125 Torino, Italy
Alfredo Soldati*
Affiliation:
Centro Interdipartimentale di Fluidodinamica e Idraulica and Dipartimento di Energetica e Macchine, Università degli Studi di Udine, via delle Scienze 208, 33100 Udine, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation (DNS) is used to study the behaviour of stably-stratified turbulent channel flow with temperature-dependent fluid properties: specifically, viscosity (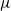) and thermal expansion coefficient (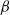). The governing equations are solved using a pseudo-spectral method for the case of turbulent water flow in a channel. A systematic campaign of simulations is performed in the shear Richardson number parameter space (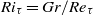, where 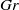is the Grashof number and 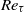the shear Reynolds number), imposing constant-temperature boundary conditions. Variations of 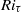are obtained by changing 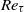and keeping 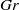constant. Independently of the value of 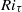, all cases exhibit an initial transition from turbulent to laminar flow. A return transition to turbulence is observed only if 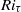is below a threshold value (which depends also on the flow Reynolds number). After the transient evolution of the flow, a statistically-stationary condition occurs, in which active turbulence and internal gravity waves (IGW) coexist. In this condition, the transport efficiency of momentum and heat is reduced considerably compared to the condition of non-stratified turbulence. The crucial role of temperature-dependent viscosity and thermal expansion coefficient is directly demonstrated. The most striking feature produced by the temperature dependence of viscosity is flow relaminarization in the cold side of the channel (where viscosity is higher). The opposite behaviour, with flow relaminarization occurring in the hot side of the channel, is observed when a temperature-dependent thermal expansion coefficient is considered. We observe qualitative and quantitative modifications of structure and wall-normal position of internal waves compared to previous results obtained for uniform or quasi-uniform fluid properties. From the trend we observe in the investigated low-Reynolds-number range, we can hypothesize that, whereas the effects of temperature-dependent viscosity may be masked at higher Reynolds number, the effects of temperature-dependent thermal expansion coefficient will persist.

JFM classification

Geophysical and Geological Flows: Internal waves Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 697 , 25 April 2012 , pp. 175 - 203
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Fluid Mechanics, CISM, 33100, Udine, Italy.

References

1. Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1.CrossRefGoogle Scholar
2. Arya, S. P. S. 1975 Buoyancy effects in an horizontal flat-plate boundary layer. J. Fluid Mech. 68, 321.CrossRefGoogle Scholar
3. Biau, D. & Bottaro, A. 2004 The effect of stable thermal stratification on shear flow stability. Phys. Fluids 16, 4742.CrossRefGoogle Scholar
4. Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1992 Direct simulation of the stably stratified turbulent Ekman layer. J. Fluid Mech. 244, 677.CrossRefGoogle Scholar
5. Fernando, H. J. S 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455.CrossRefGoogle Scholar
6. Ferziger, J. H., Koseff, J. R. & Monismith, S. G. 2002 Numerical simulation of geophysical turbulence. Comput. Fluids 31, 557.CrossRefGoogle Scholar
7. Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41, 1003.CrossRefGoogle Scholar
8. Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33, 21.CrossRefGoogle Scholar
9. Garg, R. P., Ferziger, J. H., Monismith, S. G. & Koseff, J. R. 2000 Stably stratified turbulent channel flow. I. Stratification regimes and turbulence suppression mechanism. Phys. Fluids 12, 2569.CrossRefGoogle Scholar
10. Gerz, T. & Yamazaki, H. 1993 Direct numerical simulation of buoyancy-driven turbulence in stably stratified fluid. J. Fluid Mech. 249, 415.CrossRefGoogle Scholar
11. Herbert, T. 1983 secondary instability of plane channel flow to subharmonic three-dimensional disturbances. Phys. Fluids 26, 871.CrossRefGoogle Scholar
12. Holt, S. E., Koseff, J. R. & Ferziger, J. H. 1992 A numerical study of the evolution and structure of homogeneous stably stratified sheared turbulence. J. Fluid Mech. 237, 499.CrossRefGoogle Scholar
13. Iida, O., Kasagi, N. & Nagano, Y. 2002 Direct numerical simulation of turbulent channel flow under stable density stratification. Intl J. Heat Mass Transfer 45, 1693.CrossRefGoogle Scholar
14. Incropera, F. P. & Dewitt, D. P. 1985 Fundamentals of Heat and Mass Transfer. John Wiley and Sons.Google Scholar
15. Komori, S., Ueda, H., Ogino, F. & Mizushina, T. 1983 Turbulence structure in stably stratified open-channel flow. J. Fluid Mech. 130, 13.CrossRefGoogle Scholar
16. Lessani, B. & Zainali, A. 2009 Numerical investigation of stably-stratified turbulent channel flow under non-Boussinesq conditions. J. Turbul. 10, 1.CrossRefGoogle Scholar
17. Lienhard V, J. H. & Van Atta, C. W. 1990 The decay of turbulence in thermally stratified flow. J. Fluid Mech. 210, 57.CrossRefGoogle Scholar
18. Metais, O. & Herring, J. R. 1989 Numerical simulations of the freely evolving turbulence in stably stratified fluids. J. Fluid Mech. 202, 117.CrossRefGoogle Scholar
19. Popiel, C. O. & Wojtkowiak, J. 1998 Simple formulas for thermophysical properties of liquid water for heat transfer calculations (from to ). Heat Transfer Engng 3 (19), 87.CrossRefGoogle Scholar
20. Rohr, J. J., Itsweire, E. C., Helland, K. N. & Van Atta, C. N. 1988 Growth and decay of turbulence in a stably stratified shear flow. J. Fluid Mech. 195, 77.CrossRefGoogle Scholar
21. Saiki, E. M., Biringen, S., Danabasoglu, G. & Streett, C. L. 1993 Spatial simulation of secondary instability in plane channel flow: comparison of K- and H-type disturbances. J. Fluid Mech. 253, 485.CrossRefGoogle Scholar
22. Saiki, E. M., Moeng, C. H. & Sullivan, P. P. 2000 Large-eddy simulation of the stably-stratified planetary boundary layer. Boundary-Layer Meteorol. 95, 1.CrossRefGoogle Scholar
23. Soldati, A. & Banerjee, S. 1998 Turbulence modification by large-scale organized electrohydrodynamic flows. Phys. Fluids 10, 1743.CrossRefGoogle Scholar
24. Taylor, J. R., Sarkar, S. & Armenio, V. 2005 Large eddy simulation of stably stratified open channel flow. Phys. Fluids 17, 116602.CrossRefGoogle Scholar
25. Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.CrossRefGoogle Scholar
26. van deer Lee, E. M. & Umlauf, L. 2011 Internal wave mixing in the Baltic Sea: near-inertial waves in the absence of tides. J. Geophys. Res. 116, C10016.CrossRefGoogle Scholar
27. Yeo, K., Kim, B. G. & Lee, C. 2009 Eulerian and Lagrangian statistics in stably stratified turbulent channel flows. J. Turbul. 10, 1.CrossRefGoogle Scholar
28. Zonta, F., Marchioli, C. & Soldati, A. 2012 Modulation of turbulence in forced convection by temperature-dependent viscosity. J. Fluid Mech. 697, 150–174.CrossRefGoogle Scholar