Article contents
Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow
Published online by Cambridge University Press: 15 July 2015
Abstract
The transport equation for the mean turbulent energy dissipation rate  $\overline{{\it\epsilon}}$ along the centreline of a fully developed channel flow is derived by applying the limit at small separations to the two-point budget equation. Since the ratio of the isotropic energy dissipation rate to the mean turbulent energy dissipation rate
$\overline{{\it\epsilon}}$ along the centreline of a fully developed channel flow is derived by applying the limit at small separations to the two-point budget equation. Since the ratio of the isotropic energy dissipation rate to the mean turbulent energy dissipation rate 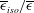 $\overline{{\it\epsilon}}_{iso}/\overline{{\it\epsilon}}$ is sufficiently close to 1 on the centreline, our main focus is on the isotropic form of the transport equation. It is found that the imbalance between the production of
$\overline{{\it\epsilon}}_{iso}/\overline{{\it\epsilon}}$ is sufficiently close to 1 on the centreline, our main focus is on the isotropic form of the transport equation. It is found that the imbalance between the production of  $\overline{{\it\epsilon}}$ due to vortex stretching and the destruction of
$\overline{{\it\epsilon}}$ due to vortex stretching and the destruction of  $\overline{{\it\epsilon}}$ caused by the action of viscosity is governed by the diffusion of
$\overline{{\it\epsilon}}$ caused by the action of viscosity is governed by the diffusion of  $\overline{{\it\epsilon}}$ by the wall-normal velocity fluctuation. This imbalance is intrinsically different from the advection-driven imbalance in decaying-type flows, such as grid turbulence, jets and wakes. In effect, the different types of imbalance represent different constraints on the relation between the skewness of the longitudinal velocity derivative
$\overline{{\it\epsilon}}$ by the wall-normal velocity fluctuation. This imbalance is intrinsically different from the advection-driven imbalance in decaying-type flows, such as grid turbulence, jets and wakes. In effect, the different types of imbalance represent different constraints on the relation between the skewness of the longitudinal velocity derivative 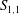 $S_{1,1}$ and the destruction coefficient
$S_{1,1}$ and the destruction coefficient 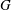 $G$ of enstrophy in different flows, thus resulting in non-universal approaches of
$G$ of enstrophy in different flows, thus resulting in non-universal approaches of 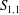 $S_{1,1}$ towards a constant value as the Taylor microscale Reynolds number,
$S_{1,1}$ towards a constant value as the Taylor microscale Reynolds number,  $R_{{\it\lambda}}$, increases. For example, the approach is slower for the measured values of
$R_{{\it\lambda}}$, increases. For example, the approach is slower for the measured values of 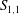 $S_{1,1}$ along either the channel or pipe centreline than along the axis in the self-preserving region of a round jet. The data for
$S_{1,1}$ along either the channel or pipe centreline than along the axis in the self-preserving region of a round jet. The data for 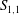 $S_{1,1}$ collected in different flows strongly suggest that, in each flow, the magnitude of
$S_{1,1}$ collected in different flows strongly suggest that, in each flow, the magnitude of 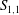 $S_{1,1}$ is bounded, the value being slightly larger than 0.5.
$S_{1,1}$ is bounded, the value being slightly larger than 0.5.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 24
- Cited by



