Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-09T22:19:00.528Z Has data issue: false hasContentIssue false
  • English
  • Français

Transmission and reflection of internal solitary waves incident upon a triangular barrier

Published online by Cambridge University Press:  23 June 2015

B. R. Sutherland ,
S. Keating  and
I. Shrivastava
B. R. Sutherland*
Affiliation:
Department of Physics, University of Alberta, Edmonton, T6G 2E1, Canada Department of Earth and Atmospheric Sciences, University of Alberta, Edmonton, T6G 2E6, Canada
S. Keating
Affiliation:
Department of Physics, University of Alberta, Edmonton, T6G 2E1, Canada
I. Shrivastava
Affiliation:
Department of Civil Engineering, IIT Bombay, Mumbai 400 076, India Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report upon laboratory experiments and numerical simulations examining the evolution of an interfacial internal solitary wave incident upon a triangular ridge whose peak lies below the interface. If the ridge is moderately large, the wave is observed to shoal and break similar to solitary waves shoaling upon a constant slope, but interfacial waves are also observed to transmit over and reflect from the ridge. In laboratory experiments, by measuring the interface displacement as it evolves in time, we measure the relative transmission and reflection of available potential energy after the incident wave has interacted with the ridge. The numerical simulations of laboratory- and ocean-scale waves measure both the available potential and kinetic energy to determine the partition of incident energy into that which is transmitted and reflected. 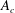From shallow-water theory, we define a critical amplitude, $A_{c}$, above which interfacial waves are unstable. The transmission is found to decrease from one to zero as the ratio of the incident wave amplitude to $A_{c}$ increases from less than to greater than one. Empirical fits are made to analytic curves through measurements of the transmission and reflection coefficients.

JFM classification

Geophysical and Geological Flows: Stratified flows Waves/Free-surface Flows: Solitary waves Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 775 , 25 July 2015 , pp. 304 - 327
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aghsaee, P., Boegman, L., Diamessis, P. J. & Lamb, K. G. 2012 Boundary-layer-separation-driven vortex shedding beneath internal solitary waves of depression. J. Fluid Mech. 690, 321–344.Google Scholar
Aghsaee, P., Boegman, L. & Lamb, K. G. 2010 Breaking of shoaling internal solitary waves. J. Fluid Mech. 659, 289–317.Google Scholar
Apel, J. R., Holbrook, J. R., Liu, A. K. & Tsai, J. J. 1985 The Sulu Sea internal soliton experiment. J. Phys. Oceanogr. 15, 1625–1651.Google Scholar
Boegman, L., Ivey, G. N. & Imberger, J. 2005 The degeneration of internal waves in lakes with sloping topography. Limnol. Oceanogr. 50, 1620–1637.CrossRefGoogle Scholar
Bourgault, D. & Kelley, D. E. 2003 Wave-induced boundary mixing in a partially mixed estuary. J. Mar. Res. 61, 553–576.Google Scholar
Bourgault, D. & Kelley, D. E. 2007 On the reflectance of uniform slopes for normally incident interfacial solitary waves. J. Phys. Oceanogr. 37, 1156–1162.Google Scholar
Chen, C.-Y. 2010 Using discriminant analysis to determine the breaking criterion for an ISW propagating over a ridge. Environ. Fluid Mech. 10, 577–586.Google Scholar
Chen, C.-Y., Hsu, J. R.-C., Cheng, M.-H., Chen, H.-H. & Kuo, C.-F. 2007 An investigation on internal solitary waves in a two-layer fluid: propagation and reflection from steep slopes. Ocean Engng 34, 171–184.Google Scholar
Chumakova, L., Menzaque, F., Milewski, P., Rosales, R., Tabak, E. & Turner, C. 2009 Stability properties and nonlinear mappings of two and three-layer stratified flows. Stud. Appl. Maths 122, 123–137.Google Scholar
Diamessis, P. J. & Redekopp, L. G. 2006 Numerical investigation of solitary internal wave-induced global instability in shallow water benthic boundary layers. J. Phys. Oceanogr. 36, 784–812.Google Scholar
Dubreil-Jacotin, M. L. 1937 Sur les théoremes d’existence relatifs aux ondes permanentes périodiques à deux dimensions dans les liquides hétérogènes. J. Math. Pures Appl. 16, 43–67.Google Scholar
El, G. A., Grimshaw, R. H. J. & Kamchatnov, A. M. 2007 Evolution of solitary waves and undular bores in shallow-water flows over a gradual slope with bottom friction. J. Fluid Mech. 585, 213–244.CrossRefGoogle Scholar
Farmer, D. M., Alford, M. H., Lien, R.-C., Yang, Y. J., Chang, M.-H. & Li, Q. 2011 From Luzon Strait to Dongsha Plateau: stages in the life of an internal wave. Oceanography 24 (4), 64–77.Google Scholar
Fructus, D., Carr, M., Grue, J., Jensen, A. & Davies, P. A. 2009 Shear-induced breaking of large internal solitary waves. J. Fluid Mech. 620, 1–29.Google Scholar
van Gastel, P., Ivey, G. N., Meuleners, M. J., Antenucci, J. P. & Fringer, O. 2009 The variability of the large-amplitude internal wave field on the Australian North West Shelf. Cont. Shelf Res. 29, 1373–1383.Google Scholar
Grimshaw, R. H. J., Pelinovsky, E., Talipova, T. & Kurkin, A. 2004 Simulation of the transformation of internal solitary waves on oceanic shelves. J. Phys. Oceanogr. 34, 2774–2791.CrossRefGoogle Scholar
Grue, J., Jensen, A., Rusås, P.-O. & Sveen, J. K. 1999 Properties of large-amplitude internal waves. J. Fluid Mech. 380, 257–278.Google Scholar
Guo, Y., Sveen, J. K., Davies, P. A., Grue, J. & Dong, P. 2004 Modelling the motion of an internal solitary wave over a bottom ridge in a stratified fluid. Environ. Fluid Mech. 4, 415–441.CrossRefGoogle Scholar
Helfrich, K. R. 1992 Internal solitary wave breaking and run-up on a uniform slope. J. Fluid Mech. 243, 133–154.CrossRefGoogle Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.Google Scholar
Hult, E. L., Troy, C. D. & Koseff, J. R. 2011a The mixing efficiency of interfacial waves breaking at a ridge: 1. Overall mixing efficiency. J. Geophys. Res. 116, C02003.Google Scholar
Hult, E. L., Troy, C. D. & Koseff, J. R. 2011b The mixing efficiency of interfacial waves breaking at a ridge: 2. Local mixing processes. J. Geophys. Res. 116, C02004.Google Scholar
Lamb, K. G. 1994 Numerical experiments of internal wave generation by strong tidal flow across a finite amplitude bank edge. J. Geophys. Res. 99, 843–864.Google Scholar
Lamb, K. G. 2002 A numerical investigation of solitary internal waves with trapped cores via shoaling. J. Fluid Mech. 451, 109–144.CrossRefGoogle Scholar
Lamb, K. G. & Wilkie, K. P. 2004 Conjugate flows for waves with trapped cores. Phys. Fluids 16, 4685–4695.Google Scholar
Lamb, K. G. & Yan, L. 1996 The evolution of internal wave undular bores: comparison of a fully-nonlinear numerical model with weakly nonlinear theories. J. Phys. Oceanogr. 26, 2712–2734.Google Scholar
Long, R. R. 1953 Some aspects of the flow of stratified fluids: a theoretical investigation. Tellus 5, 42–58.Google Scholar
Long, R. R. 1956 Solitary waves in one- and two-fluid systems. Tellus 8, 460–471.Google Scholar
Maderich, V., Talipova, T., Grimshaw, R., Pelinovsky, E., Choi, B., Brovchenko, I., Terletska, K. & Kim, D. C. 2009 The transformation of an interfacial solitary wave of elevation at a bottom step. Nonlinear Process. Geophys. 16, 33–42.CrossRefGoogle Scholar
Maderich, V., Talipova, T., Grimshaw, R., Terletska, K., Brovchenko, I., Pelinovsky, E. & Choi, B. 2010 Interaction of a large amplitude interfacial solitary wave of depression with a bottom step. Phys. Fluids 22, 076602.Google Scholar
Mercier, M. J., Garnier, N. B. & Dauxois, T. 2008 Reflection and diffraction of internal waves analyzed with the Hilbert transform. Phys. Fluids 20, 086601.CrossRefGoogle Scholar
Michallet, H. & Ivey, G. N. 1999 Experiments on mixing due to internal solitary waves breaking on uniform slopes. J. Geophys. Res. 104, 13467–13477.Google Scholar
Milewski, P., Tabak, E., Turner, C., Rosales, R. & Menzaque, F. 2004 Nonlinear stability of two-layer flows. Commun. Math. Sci. 2 (3), 427–442.Google Scholar
New, A. L. & Pingree, R. D. 1992 Local generation of internal soliton packets in the central Bay of Biscay. Deep-Sea Res. 39 (9), 1521–1534.CrossRefGoogle Scholar
Osborne, A. R. & Burch, T. L. 1980 Internal solitons in the Andaman Sea. Science 208, 451–460.Google Scholar
Pinkel, R. 2000 Internal solitary waves in the warm pool of the western equatorial Pacific. J. Phys. Oceanogr. 30, 2906–2926.Google Scholar
Reeder, D. B., Ma, B. B. & Yang, Y. J. 2011 Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Mar. Geol. 279, 12–18.Google Scholar
Richards, C., Bourgault, D., Galbraith, P. S., Hay, A. & Kelley, D. E. 2013 Measurements of shoaling internal waves and turbulence in an estuary. J. Geophys. Res. 118, 273–286.CrossRefGoogle Scholar
Sandstrom, H. & Elliott, J. A. 1984 Internal tide and solitons on the Scotian Shelf: a nutrient pump at work. J. Geophys. Res. 89, 6415–6426.Google Scholar
Sutherland, B. R., Barrett, K. J. & Ivey, G. N. 2013 Shoaling internal solitary waves. J. Geophys. Res. 118, 1–14.Google Scholar
Sveen, J. K., Guo, Y., Davies, P. A. & Grue, J. 2002 On the breaking of internal solitary waves at a ridge. J. Fluid Mech. 469, 161–188.Google Scholar
Vlasenko, V. & Hutter, K. 2002 Numerical experiments on the breaking of solitary internal waves over a slope-shelf topography. J. Phys. Oceanogr. 32, 1779–1793.Google Scholar
White, B. L. & Helfrich, K. R. 2008 Gravity currents and internal waves in a stratified fluid. J. Fluid Mech. 616, 327–356.Google Scholar
Xu, J., Xie, J., Chen, Z., Cai, S. & Long, X. 2012 Enhanced mixing induced by internal solitary waves in the South China Sea. Cont. Shelf Res. 49, 34–43.Google Scholar

Sutherland et al. supplementary movie

Movie corresponding to experiment shown in Figure 3a

Download Sutherland et al. supplementary movie(Video)
Video 4.5 MB

Sutherland et al. supplementary movie

Movie corresponding to experiment shown in Figure 3a

Download Sutherland et al. supplementary movie(Video)
Video 2.3 MB

Sutherland et al. supplementary movie

Movie corresponding to experiment shown in Figure 3b

Download Sutherland et al. supplementary movie(Video)
Video 5.9 MB

Sutherland et al. supplementary movie

Movie corresponding to experiment shown in Figure 3b

Download Sutherland et al. supplementary movie(Video)
Video 3 MB

Sutherland et al. supplementary movie

Movie corresponding to simulation shown in figure 7

Download Sutherland et al. supplementary movie(Video)
Video 5.6 MB

Sutherland et al. supplementary movie

Movie corresponding to simulation shown in figure 7

Download Sutherland et al. supplementary movie(Video)
Video 1.8 MB

Sutherland et al. supplementary movie

Movie corresponding to simulation shown in figure 10

Download Sutherland et al. supplementary movie(Video)
Video 3 MB

Sutherland et al. supplementary movie

Movie corresponding to simulation shown in figure 10

Download Sutherland et al. supplementary movie(Video)
Video 1.2 MB