Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T18:09:05.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitions to different kinds of turbulence in a channel with soft walls

Published online by Cambridge University Press:  01 June 2017

S. S. Srinivas  and
V. Kumaran Open the ORCID record for V. Kumaran [Opens in a new window]
S. S. Srinivas
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow in a rectangular channel with walls made of polyacrylamide gel is experimentally studied to examine the effect of soft walls on transition and turbulence. The bottom wall is fixed to a substrate and the top wall is unrestrained. As the Reynolds number increases, two different flow regimes are observed. The first is the ‘soft-wall turbulence’ (Srinivas & Kumaran, J. Fluid Mech., vol. 780, 2015, pp. 649–686). There is a large increase in the magnitudes of the velocity fluctuations after transition and the fluid velocity fluctuations appear to be non-zero at the soft walls, although higher resolution measurements are required to establish the nature of the boundary dynamics. The fluid velocity fluctuations are symmetric about the centreline of the channel, and they show relatively little downstream variation. The wall displacement measurements indicate that there is no observable motion perpendicular to the surface to within the experimental resolution, but displacement fluctuations parallel to the surface are observed after transition. As the Reynolds number is further increased, there is a second ‘wall-flutter’ transition, which involves visible downstream travelling waves in the top (unrestrained) wall alone. Wall displacement fluctuations of frequency less than approximately 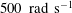$500~\text{rad}~\text{s}^{-1}$ are observed both parallel and perpendicular to the wall. The mean velocity profiles and turbulence intensities are asymmetric, with much larger turbulence intensities near the top wall. The transitions are observed in sequence from a laminar flow at Reynolds number less than 1000 for a channel of height 0.6 mm and from a turbulent flow at a Reynolds number greater than 1000 for a channel of height 1.8 mm.

JFM classification

Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 267 - 306
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. 1960 Effects of a flexible boundary on hydrodynamic stability. J. Fluid Mech. 9, 513–532.Google Scholar
Benjamin, T. B. 1963 The three-fold classification of unstable disturbances in flexible surfaces bounding an inviscid flow. J. Fluid Mech. 16, 436–450.Google Scholar
Carpenter, P. W. & Garrad, A. D. 1985 The hydrodynamic stability of the flow over kramer-type compliant surfaces. Part 1. Tollmien–Schlichting instability. J. Fluid Mech. 155, 465–510.CrossRefGoogle Scholar
Carpenter, P. W. & Garrad, A. D. 1986 The hydrodynamic stability of the flow over kramer-type compliant surfaces. Part 2. Flow induced surface instability. J. Fluid Mech. 170, 199–232.CrossRefGoogle Scholar
Chokshi, P. P. & Kumaran, V. 2008 Weakly nonlinear analysis of viscous instability in flow past a neo-hookean surface. Phys. Rev. E 77, 056303.Google Scholar
Chokshi, P. P. & Kumaran, V. 2009 Weakly nonlinear stability analysis of a flow past a neo-hookean solid at arbitrary reynolds numbers. Phys. Fluids 21, 014109.Google Scholar
Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.CrossRefGoogle Scholar
Eggert, M. D. & Kumar, S. 2004 Observations of instability, hysteresis and osciallations in low-Reynolds-number flow past polymer gels. J. Colloid Interface Sci. 274, 238–242.Google Scholar
Gad-el Hak, M., Blackwelder, R. F. & Riley, J. J. 1985 On the interaction of compliant coatings with boundary layer flows. J. Fluid Mech. 140, 257–280.Google Scholar
Gaurav & Shankar, V. 2009 Stability of fluid flow through deformable neo-hookean tubes. J. Fluid Mech. 627, 291–322.Google Scholar
Gaurav & Shankar, V. 2010 Stability of pressure-driven flow in a deformable neo-hookean channel. J. Fluid Mech. 659, 318–350.Google Scholar
George, W. K. 2007 Is there a universal log law for turbulent wall-bounded flows? Phil. Trans. R. Soc. Lond. A 365, 789–806.Google Scholar
Gkanis, V. & Kumar, S. 2003 Instability of creeping couette flow past a neo-hookean solid. Phys. Fluids 15, 2864–2871.Google Scholar
Gkanis, V. & Kumar, S. 2005 Stability of pressure driven creeping flows in channels lined with a nonlinear elastic solid. J. Fluid Mech. 524, 357–375.Google Scholar
Gkanis, V. & Kumar, S. 2006 Instability of creeping flow past a deformable wall: the role of depth-dependent modulus. Phys. Rev. E 73, 026307.Google Scholar
Goswami, P. S. & Kumaran, V. 2011 Particle dynamics in the channel flow of a turbulent particle-gas suspension at high stokes number. Part 1. DNS and fluctuating force model. J. Fluid Mech. 687, 1–40.CrossRefGoogle Scholar
Hansen, R. J. & Hunston, D. L. 1974 An experimental study of fluid turbulence over compliant surfaces. J. Sound Vib. 34, 297–308.Google Scholar
Hansen, R. J. & Hunston, D. L. 1983 Fluid-property effects on flow-generated waves on compliant surfaces. J. Fluid Mech. 133, 161–177.Google Scholar
Hof, B., Juel, A. & Mullin, T. 2003 Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91, 244502.Google Scholar
Hoya, S. & Jimenez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to re 𝜏 = 2003. Phys. Fluids 19, 011702.Google Scholar
Krindel, P. & Silberberg, A. 1979 Flow through gel-walled tubes. J. Colloid Interface Sci. 71, 39–50.Google Scholar
Kumaran, V. 1995 Stability of the viscous flow of a fluid through a flexible tube. J. Fluid Mech. 294, 259–281.Google Scholar
Kumaran, V. 1996 Stability of an inviscid flow in a flexible tube. J. Fluid Mech. 320, 1–17.Google Scholar
Kumaran, V. 1998 Stability of wall modes in a flexible tube. J. Fluid Mech. 362, 1–15.Google Scholar
Kumaran, V. 2000 Classification of instabilities in the flow past flexible surfaces. Curr. Sci. 79, 766–773.Google Scholar
Kumaran, V. 2003 Hydrodynamic stability of flow through compliant channels and tubes. In The Proceedings of IUTAM Symposium on Flow in Collapsible Tubes and Past Other Highly Compliant Boundaries (ed. Carpenter, P. W. & Pedley, T. J.), Kluwer Academic Publishers.Google Scholar
Kumaran, V. 2015 Experimental studies on the flow through soft tubes and channels. Sadhana 40, 911–923.CrossRefGoogle Scholar
Kumaran, V. & Bandaru, P. 2016 Ultra-fast microfluidic mixing by soft-wall turbulence. Chem. Engng Sci. 149, 156–168.Google Scholar
Kumaran, V., Fredrickson, G. H. & Pincus, P. 1994 Flow induced instability at the interface between a fluid and a gel at low reynolds number. J. Phys. Paris II 4, 893–911.Google Scholar
Kumaran, V. & Muralikrishnan, R. 2000 Spontaneous growth of fluctuations in the viscous flow of a fluid past a soft interface. Phys. Rev. Lett. 84, 3310–3313.Google Scholar
Lahav, J., Eliezer, N. & Silberberg, A. 1973 Gel-walled cylindrical channels as models for the microcirculation: dynamics of flow. Biorheology 10, 595–604.CrossRefGoogle ScholarPubMed
Landahl, M. T. 1962 On the stability of a laminar incompressible boundary layer over a flexible surface. J. Fluid Mech. 13, 609–632.Google Scholar
Muralikrishnan, R. & Kumaran, V. 2002 Experimental study of the instability of the viscous flow past a flexible surface. Phys. Fluids 14, 775–780.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von krmn coefficient in canonical flows. Phys. Fluids 20, 101518.Google Scholar
Panton, R. L. 1984 Incompressible Flow. Wiley.Google Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2, 1–95.Google Scholar
Shankar, V. 2015 Stability of fluid flow through deformable tubes and channels: an overview. Sadhana 40, 925–943.Google Scholar
Shankar, V. & Kumar, S. 2004 Instability of viscoelastic plane couette flow past a deformable wall. J. Non-Newtonian Fluid Mech. 116, 371–393.Google Scholar
Shankar, V. & Kumaran, V. 1999 Stability of non-parabolic flows in a flexible tube. J. Fluid Mech. 395, 211–236.Google Scholar
Shankar, V. & Kumaran, V. 2000 Stability of non-axisymmetric modes in a flexible tube. J. Fluid Mech. 407, 291–314.Google Scholar
Shankar, V. & Kumaran, V. 2001 Asymptotic analysis of wall modes in a flexible tube revisited. Eur. Phys. J. B 19, 607–622.Google Scholar
Shankar, V. & Kumaran, V. 2002 Stability of wall modes in the flow past a flexible surface. Phys. Fluids 14, 2324–2338.Google Scholar
Shrivastava, A., Cussler, E. L. & Kumar, S. 2008 Mass transfer enhancement due to a soft elastic boundary. Chem. Engng Sci. 63, 4302–4305.CrossRefGoogle Scholar
Srinivas, S. S. & Kumaran, V. 2015 After transition in a soft-walled microchannel. J. Fluid Mech. 780, 649–686.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Verma, M. K. S. & Kumaran, V. 2012 A dynamical instability due to fluid-wall coupling lowers the transition Reynolds number in the flow through a flexible tube. J. Fluid Mech. 705, 322–347.Google Scholar
Verma, M. K. S. & Kumaran, V. 2013 A multifold reduction in the transition Reynolds number, and ultra-fast mixing, in a micro-channel due to a dynamical instability induced by a soft wall. J. Fluid Mech. 727, 407–455.Google Scholar
Verma, M. K. S. & Kumaran, V. 2015 Stability of the flow in a soft tube deformed due to an applied pressure gradient. Phys. Rev. E 91, 043001.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar
Zang, L., Balachandar, S. & Fisher, P. 2005 Wall-induced forces on a rigid sphere at finite Reynolds number. J. Fluid Mech. 536, 1–25.Google Scholar